Skalad korrelation

Inom statistik är skalad korrelation en form av en korrelationskoefficient som är tillämplig på data som har en tidsmässig komponent såsom tidsserier . Det är den genomsnittliga kortsiktiga korrelationen. Om signalerna har flera komponenter (långsamma och snabba), kan den skalade korrelationskoefficienten beräknas endast för de snabba komponenterna i signalerna, och ignorerar bidragen från de långsamma komponenterna. Denna filtreringsliknande operation har fördelarna av att inte behöva göra antaganden om signalernas sinusformade natur.

I studier av hjärnsignaler är forskare till exempel ofta intresserade av högfrekvenskomponenterna (beta- och gammaområde; 25–80 Hz), och kanske inte är intresserade av lägre frekvensområden (alfa, theta, etc.). I det fallet kan skalad korrelation beräknas endast för frekvenser högre än 25 Hz genom att välja skalan för analysen, s , för att motsvara perioden för den frekvensen (t.ex. s = 40 ms för 25 Hz oscillation).

Definition

Skalad korrelation mellan två signaler definieras som den genomsnittliga korrelationen beräknad över korta segment av dessa signaler. Först är det nödvändigt att bestämma antalet segment $K$ som kan passa in i den totala längden $T$ för signalerna för en given skala $s$ :

K=\operatörsnamn {runda} \left({\frac {T}{s}}\höger).

Därefter, om $r_{k}$ är Pearsons korrelationskoefficient för segment $k$ , den skalade korrelationen över hela signalen ${\bar {r}}_{s }$ beräknas som

{\bar {r}}_{s}={\frac {1}{K}}\sum \limits _{k=1}^{K}r_{k}.

Effektivitet

I en detaljerad analys, Nikolić et al. visade att graden till vilken bidragen från de långsamma komponenterna kommer att dämpas beror på tre faktorer, valet av skala, amplitudförhållandena mellan den långsamma och snabba komponenten och skillnaderna i deras svängningsfrekvenser. Ju större skillnaderna är i oscillationsfrekvenser, desto mer effektivt kommer bidragen från de långsamma komponenterna att tas bort från den beräknade korrelationskoefficienten. På liknande sätt, ju mindre kraften hos långsamma komponenter är i förhållande till de snabba komponenterna, desto bättre presterar den skalade korrelationen.

Tillämpning på korskorrelation

Exempel på ett korskorrelogram mellan spiktåg beräknat på ett klassiskt sätt (vänster) och genom att använda skalad korrelation (höger;

s

= 200 ms). Skalad korrelation tar bort den långsamma komponenten från korskorrelogrammet.

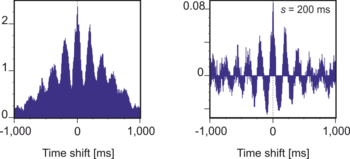
Skalad korrelation kan tillämpas på auto- och korskorrelation för att undersöka hur korrelationer av högfrekventa komponenter förändras vid olika tidsfördröjningar. För att korrekt beräkna korsskalad korrelation för varje tidsförskjutning är det nödvändigt att segmentera signalerna på nytt efter varje tidsförskjutning. Med andra ord skiftas signaler alltid innan segmenteringen tillämpas. Skalad korrelation har senare använts för att undersöka synkroniseringsnav i den visuella cortexen Skalad korrelation kan också användas för att extrahera funktionella nätverk.

Fördelar jämfört med filtreringsmetoder

Skalad korrelation bör i många fall föredras framför signalfiltrering baserad på spektrala metoder. Fördelen med skalad korrelation är att den inte gör antaganden om signalens spektrala egenskaper (t.ex. sinusformade signaler). Nikolić et al. har visat att användningen av Wiener-Khinchin-satsen för att ta bort långsamma komponenter är sämre än resultat som erhålls genom skalad korrelation. Dessa fördelar blir uppenbara särskilt när signalerna är icke-periodiska eller när de består av diskreta händelser såsom tidsstämplarna vid vilka neuronala aktionspotentialer har detekterats.

Relaterade metoder

En detaljerad inblick i en korrelationsstruktur över olika skalor kan ges genom visualisering med multiupplösningskorrelationsanalys.

Se även

Gratis källor

En gratis källkod för beräkning av skalad korskorrelation och ett gränssnitt för MATLAB kan laddas ner här: http://www.raulmuresan.ro/sources/corrlib/
Enkel demokod i python: https://github.com/dankonikolic/Scaled-Correlation