Sinuositet

Beräkning av sinusitet för en oscillerande kurva.

Snören på bergsväg med hög sinusitet vid Luz Ardiden

Den slingrande Rio Cauto vid Guamo Embarcadero, Kuba , tar inte den kortaste vägen nerför. Därför är dess sinusitetsindex > 1.

Två skidspår med olika grad av sinusitet i samma backe

Sinuositet , sinuositetsindex eller sinuositetskoefficient för en kontinuerligt differentierbar kurva som har minst en inflexionspunkt är förhållandet mellan den kurvlinjära längden (längs kurvan) och det euklidiska avståndet ( rät linje ) mellan kurvans ändpunkter. Denna dimensionslösa kvantitet kan också omformuleras som den "verkliga väglängden" dividerad med den "kortaste väglängden" för en kurva. Värdet sträcker sig från 1 (fallet med rät linje) till oändligt (fallet med en sluten slinga, där den kortaste väglängden är noll eller för en oändligt lång faktisk väg).

Tolkning

Kurvan måste vara kontinuerlig (inget hopp) mellan de två ändarna. Sinuositetsvärdet är verkligen signifikant när linjen är kontinuerligt differentierbar (ingen vinkelpunkt). Avståndet mellan båda ändarna kan också utvärderas av ett flertal segment enligt en streckad linje som går genom de på varandra följande inflexionspunkterna (sinuositet av ordning 2).

Beräkningen av sinusiteten är giltig i ett 3-dimensionellt utrymme (t.ex. för tunntarmens centrala axel ) , även om det ofta utförs i ett plan (med då en möjlig ortogonal projektion av kurvan i den valda planen; "klassisk " sinuositet på horisontalplanet, longitudinell profil sinuositet på vertikalplanet).

Klassificeringen av en sinusitet (t.ex. stark/svag) beror ofta på kurvans kartografiska skala (se kustlinjeparadoxen för ytterligare detaljer) och på objektets hastighet som strömmar genom den (flod, lavin, bil, cykel, bobsläde, skidåkare, höghastighetståg, etc.): sinusiteten hos samma krökta linje kan anses vara mycket stark för ett höghastighetståg men låg för en flod. Ändå är det möjligt att se en mycket stark sinusitet i följden av få flodböjar, eller av snören på vissa bergsvägar.

Anmärkningsvärda värden

Sinuositeten S för:

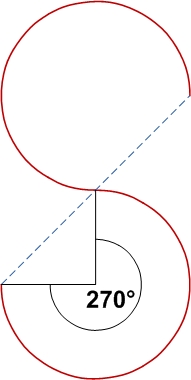
• 2 inverterade kontinuerliga halvcirklar placerade i samma plan är $S={\tfrac {\pi }{2}}\approx 1,5708...$ . Den är oberoende av cirkelradien;
• en sinusfunktion (över ett helt antal n halvperioder), som kan beräknas genom att beräkna sinuskurvans båglängd på dessa perioder, är $S=\textstyle {\tfrac {1}{n\pi }}\int _{0}^{n\pi }{\sqrt {1+(\cos x)^{2}} }dx\approx 1,216...$

Exempel med 270° vinkel

Med liknande motsatta bågar leder i samma plan, kontinuerligt differentierbara:

Central vinkel		Sinuositet
Grader	Radianer	Exakt	Decimal
30°	${\frac {\pi }{6}}$	${\frac {\pi }{3({\sqrt {6}}-{\sqrt {2}})}}$	1,0115
60°	${\frac {\pi }{3}}$	${\frac {\pi }{3}}$	1,0472
90°	${\frac {\pi }{2}}$	${\frac {\pi }{2{\sqrt {2}}}}$	1,1107
120°	${\frac {2\cdot \pi }{3}}$	${\frac {2\cdot \pi }{3{\sqrt {3}}}}$	1,2092
150°	${\frac {5\cdot \pi }{6}}$	${\frac {5\cdot \pi }{3({\sqrt {6}}+{\sqrt {2}})}}$	1,3552
180°	$\pi$	${\frac {\pi }{2}}$	1,5708
210°	${\frac {7\cdot \pi }{6}}$	${\frac {7\cdot \pi }{3({\sqrt {6}}+{\sqrt {2}})}}$	1,8972
240°	${\frac {4\cdot \pi }{3}}$	${\frac {4\cdot \pi }{3{\sqrt {3}}}}$	2,4184
270°	${\frac {3\cdot \pi }{2}}$	${\frac {3\cdot \pi }{2{\sqrt {2}}}}$	3,3322
300°	${\frac {5\cdot \pi }{3}}$	${\frac {5\cdot \pi }{3}}$	5,2360
330°	${\frac {11\cdot \pi }{6}}$	${\frac {11\cdot \pi }{3({\sqrt {6}}-{\sqrt {2}})}}$	11,1267

floder

I studier av floder är sinusitetsindexet liknande men inte identiskt med den allmänna formen ovan, givet av:

${\text{SI}}={\frac {\text{kanallängd}}{\text{downdallängd}}}$

Skillnaden från den allmänna formen beror på att dalgången inte är helt rak. Sinuositetsindexet kan då förklaras som avvikelserna från en bana som definieras av riktningen för den maximala nedåtlutningen. Av denna anledning har berggrundsströmmar som rinner direkt nedför sluttningen ett sinusitetsindex på 1, och slingrande vattendrag har ett sinusitetsindex som är större än 1.

Det är också möjligt att särskilja fallet där strömmen som strömmar på linjen inte fysiskt kunde färdas avståndet mellan ändarna: i vissa hydrauliska studier leder detta till att tilldela ett sinuositetsvärde på 1 för en ström som flyter över stenig berggrund längs en horisontell rätlinjig projektion, även om lutningsvinkeln varierar.

För floder är de konventionella klasserna av sinuositet, SI:

• SI <1,05: nästan rak
• 1,05 ≤ SI <1,25: lindning
• 1,25 ≤ SI <1,50: vridet
• 1,50 ≤ SI: slingrande

Det har hävdats att flodformer styrs av ett självorganiserande system som gör att deras genomsnittliga sinuositet (mätt i termer av avstånd från källa till mun, inte kanallängd) är π , men detta har inte bekräftats senare studier som fann ett medelvärde mindre än 2.

Se även

• Krökning
• Oxbow sjö