Serpentiler

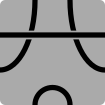
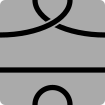
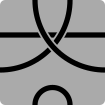
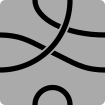
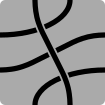
Serpentiles är namnet som myntats av Kurt N. Van Ness för de hexagonala brickorna som används i olika abstrakta strategispel med kantmatchande pusselkopplingar, som Psyche -Paths , Kaliko och Tantrix . För varje bricka används en till tre färger för att rita banor som länkar samman de sex sidorna i olika konfigurationer. Varje sida är ansluten till en annan sida med en specifik vägväg och färg. Spelet fortsätter i allmänhet så att spelarna turas om att lägga brickor. Under varje varv läggs en bricka i anslutning till befintliga plattor så att färgade banor hänger samman över kakelkanterna.

Serpentiles är också namnet på ett pusselkopplingsspel för en spelare utvecklat av Brett J. Gilbert och publicerat av ThinkFun 2008. Spelet Serpentiles (2008) innehåller fyrkantiga (1×1) och rektangulära (2×1) brickor och utmaningskort som ger en lista över brickor som bör arrangeras för att göra en sammanhängande bana.

Kakelnotation

Van Ness myntade också en tresiffrig notation för brickkategorier, baserad på banorna som visas på brickorna. Notationen xyz syftar på:

• x = antal banor som förbinder sidor med angränsning 3, 2 segment från varandra (motstående sidor)
• y = antal banor som förbinder sidor med angränsning 2, 1 segment från varandra
• z = antal banor som länkar sidor med angränsning 1, 0 segment från varandra (intilliggande sidor)

Det bör vara tydligt att angränsning 3 är max. Eftersom det finns sex sidor finns det tre banor mellan sidorna, och summan av siffrorna i notationen är alltid tre. Van Ness publicerade också en matematisk beskrivning: $\sum _{n=1}^{3}10^{n-1}a_{n}$ där ${ \displaystyle a_{n}}$ är antalet segment med närliggande $n$ . Det finns fem distinkta kombinationer av sex sidor och tre banor, som för närvarande ignorerar möjligheten att ändra banans färg:

• 6S3P: Sexsidiga polygoner med tre banor
• 

  003 , vilket indikerar att vägarna länkar tre intilliggande sidor

• 

  021 , vilket indikerar att banorna länkar en intilliggande sida och två sidor med ett segment isär

• 

  102 , vilket indikerar att banorna länkar två intilliggande sidor och en uppsättning motsatta sidor

• 

  120 , vilket indikerar att banorna länkar två sidor med ett segment isär och en uppsättning motsatta sidor

• 

  300 , vilket indikerar att vägarna länkar samman den kompletta uppsättningen av tre motsatta sidor

Roterande position

En ortogonal rotation som lämnar hexagonen i samma orientering (med platta sidor till vänster och höger) är 60°. Det finns sex potentiella ortogonala rotationspositioner (360°/60°) för den vanliga sexsidiga sexkanten. Vid undersökning 300 rotationssymmetri: varje rotation på 60° kommer att resultera i att samma sidor länkas ihop, så 0300 har en unik rotationsposition. På samma sätt 003 två unika rotationspositioner; en rotation på 60° kommer att resultera i att olika sidor länkas samman av banorna, men en andra rotation på 60° i samma riktning kommer att resultera i att de ursprungliga sidorna länkas igen. På liknande sätt 102 och 120 båda tre unika rotationspositioner och 021 har sex unika rotationspositioner.

Ortogonala rotationer av 003

Orientering 12-34-56

Orientering 23-45-61, efter en ortogonal rotation

För att unikt beskriva varje rotationsposition, föreställ dig att en referensram används där varje sida är numrerad från 1 till 6 sekventiellt moturs. Banorna som förbinder sidorna kan beskrivas som länkade par.

Till exempel, för 003 ovan, fortsätter man moturs från den nedre högra kanten, är ban-/parnotationen 12-34-56. En enda ortogonal rotation av formen kommer att lägga till en (om moturs) eller subtrahera en (om medurs) till varje tal, modulo 6. På detta sätt skulle de länkade banorna med en ortogonal rotation (60°) moturs ändras till 23-45-67, eller omskrivning med modulo 6, 23-45-61, vilket visar att olika sidor är länkade med en enda ortogonal rotation. Den specifika ordningen inom ett par och ordningen som paren skrivs i påverkar inte konfigurationen. Till exempel motsvarar 23-45-61 23-45-16 och 16-23-45. Således med en andra ortogonal rotation, som resulterar i 34-56-12, är det enkelt att visa att den andra ortogonala rotationen motsvarar 12-34-56, den ursprungliga orienteringen.

Referensramen kan också numreras sekventiellt medurs. I så fall skulle en medurs rotation öka värdena med 1, medan en moturs rotation skulle minska värdena med 1. Orienteringen av referensramen (medsols eller moturs) påverkar bara den aritmetik som krävs för att rotera brickan. På samma sätt är valet av ursprung (vilken sida som betecknas som den första sidan) för referensramen godtyckligt, men referensramen förblir fixerad under rotation.

Klass	Unika rotationspositioner _	Galleri med positioner
003	2	12-34-56 23-45-61
021	6	15-26-34 26-31-45 31-42-56 42-53-61 53-64-12 64-15-23
102	3	16-25-34 21-36-45 32-41-56
120	3	13-25-46 24-36-51 35-41-62
300	1	14-25-36

Att beskriva brickorna med länkade sidor inkluderar också implicit den tresiffriga Van Ness-notationen. För varje godtycklig treparsekvens AB - CD - EF kan Van Ness-notationen återställas med följande formel: $10^{[min(\left\vert BA\right\vert ,6-\left\vert BA\right\vert )-1]{\bmod {3}}}+10^{[min (\left\vert DC\right\vert ,6-\left\vert DC\right\vert )-1]{\bmod {3}}}+10^{[min(\left\vert FE\right\vert ,6-\left\vert FE\right\vert )-1]{\bmod {3}}}$

Vanlig 4-sidig fyrkant

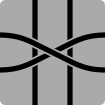
Även om en vanlig sexsidig polygon (hexagon) kan användas för att täcka en plan yta utan mellanrum, kan en vanlig fyrsidig polygon (kvadrat) också användas. Fyrkanten med två banor som länkar sidor kan beskrivas på ett liknande sätt, med en tvåsiffrig notation yz ; det finns bara två potentiella konfigurationer.

• 4S2P: Fyrsidiga polygoner med två banor
• 

  02 , vilket indikerar att vägarna länkar två intilliggande sidor

• 

  20 , vilket indikerar att vägarna länkar två motsatta sidor

Liksom det hexagonala fallet har 20 (där alla banor länkar motsatta sidor) rotationssymmetri. Det är tydligt att 02 inte har rotationssymmetri, eftersom att rotera plattan 90° medurs eller moturs kommer att länka ihop olika sidor. Jämför med samma bricka roterad 90°: Fyrkantiga brickor som saknar rotationssymmetri är kända som Truchet-plattor , som beskrivs i en memoar från 1704 av Sébastien Truchet med titeln "Mémoire sur les combinaisons" och populariserades 1987 av Cyril Stanley Smith .

Vanlig 8-sidig oktagon

På samma sätt kan en vanlig åttasidig polygon (oktagon) ha fyra banor som parar ihop de åtta sidorna, beskrivna med Van Ness notation på ett liknande sätt med en fyrsiffrig notation wxyz . Det finns 18 olika kombinationer:

• 8S4P: Åttasidiga polygoner med fyra banor
• 

  0004

• 

  0022

• 

  0040

• 

  0103

• 

  0121 (a)

• 

  0121 (b)

• 

  0202

• 

  0220

• 

  0301

• 

  0400

• 

  1012

• 

  1111 (a)

• 

  1111 (b)

• 

  1210

• 

  2002

• 

  2020

• 

  2200

• 

  4000

Liksom med de föregående exemplen med hexagon och kvadrat, har fallet som förbinder alla motsatta sidor ( 4000 ) rotationssymmetri. Observera att för oktagonen beskriver notationen inte längre vägkonfigurationen unikt. Det finns två dubbletter av notationer i galleriet: 0121 och 1111 . 1111 - paret är spegelbilder. Rotationspositionsbeteckningen kan användas för att särskilja dessa brickor; med en referensram numrerad moturs från den nedre kanten 0121 (a) ovan skrivas som " 0121 12-36-47-68", vilket är skilt från 0121 (b): " 0121 12-38-46 -57". Likaså är 1111 (a) " 1111 12-36-48-57", skild från 1111 (b): " 1111 13-25-48-67". Med hjälp av modulär aritmetik (modulo 8) 1111 (a) och (b) var och en roteras med en ortogonal rotation (45°) moturs till positionerna "15-24-36-78" och "15-68-47- 23", vilket visar deras parade reflekterande symmetri.

Dessa åttakantiga plattor skulle kunna kombineras med de fyrkantiga plattorna som beskrivs här (roterade 45° för att fylla de mellanliggande utrymmena) för att helt belägga en yta med banor över alla kanter.

Regelbundna polygoner med 2 ingångspunkter per sida

Den föregående diskussionen täckte fallen med vanliga 4-, 6- och 8-sidiga polygoner med en enda ingångspunkt per sida, med varje sida sammanlänkad med en väg. Eftersom banorna länkar två olika sidor, kräver användning av en enda ingångspunkt per sida regelbundna 2n -sidiga polygoner med ett jämnt antal sidor för att säkerställa att alla ingångspunkter är länkade av banor. Om det finns brickor med ett udda antal sidor, skulle ett jämnt antal ingångspunkter på samma sätt säkerställa att alla ingångspunkter är länkade med banor.

• 3S3P: Tresidiga polygoner med tre banor
• 

  003 (a) 12-34-56

• 

  003 (b) 16-23-45

• 

  021 (a) 12-35-46

• 

  021 (b) 13-26-45

• 

  102 12-36-45

• 

  120 15-24-36

• 

  300 14-25-36

Både 003 (a) och (b) återges här; (b) varianten återvinns av den inskrivna triangeln.

Till exempel kan en vanlig 3-sidig polygon (liksidig triangel) ha 2 ingångspunkter per sida. Det finns 7 potentiella kombinationer med 3 banor per bricka, avbildad ovan. Även om Van Ness-notationen kan tillämpas genom att modifiera den för att räkna intilliggande snarare än sidor, beskrivs inte varje bricka unikt av Van Ness-notationen, även om förhållandet mellan 003 ( a ) och (b) fallen kan ses genom att skriva in en triangel, som exemplet som visas här. En liknande triangel skulle kunna skrivas in för 021 (a) för att visa dess förhållande till 021 (b).

Det kan vara enklare att beskriva brickan med vägpar istället. I uppsättningen av tresidiga brickor med två ingångspunkter per sida och tre banor, börjar numreringen från den vänstra punkten på den nedre kanten och fortsätter sekventiellt moturs.

En hel rotation vrider brickan 120° (=360°/3 sidor). Rotationsaritmetik utförs genom att lägga till två, modulo sex. Tänk på brickan (12-34-56). Att rotera brickan en eller flera fullständiga rotationer kommer, genom inspektion, inte att ändra de punkter som är länkade. För att demonstrera detta resulterar en rotation moturs i konfigurationen (34-56-78), eller, efter att modularitmetiken har utförts, (34-56-12), som kan omarrangeras till (12-34-56) , vilket visar att en rotation inte påverkar de länkade banorna och så det finns en distinkt rotationsposition för denna bricka. Å andra sidan, överväg brickan (13-26-45). De första två rotationerna moturs av denna bricka resulterar i konfigurationerna (16-24-35) respektive (15-23-46), så denna bricka har tre distinkta rotationspositioner.

På samma sätt har en vanlig 4-sidig polygon (fyrkant) med 2 ingångspunkter per sida 35 potentiella kombinationer med 4 banor per bricka. Den fullständiga rotationen är 90° och rotationssymmetrin kan bestämmas genom att addera 2, modulo 8 på ett sätt som liknar det för det liksidiga triangelfallet ovan. Denna uppsättning av fyrsidiga polygoner med två ingångspunkter per sida och fyra banor per bricka används i det kommersiella brädspelet Tsuro .

• 4S4P: Fyrsidiga polygoner med fyra banor
• 

  0004 (a) 12-34-56-78

• 

  0004 (b) 18-23-45-67

• 

  0022 (a) 12-34-57-68

• 

  0022 (b) 18-23-46-57

• 

  0040 (a) 17-24-35-68

• 

  0040 (b) 17-28-35-46

• 

  0103 (a) 12-34-58-67

• 

  0103 (b) 12-38-45-67

• 

  0121 (a) 12-35-47-68

• 

  0121 (b) 17-23-46-58

• 

  0121 (x) 12-38-46-57

• 

  0121 (y) 17-28-36-45

• 

  0202 (a) 12-38-47-56

• 

  0202 (b) 18-27-36-45

• 

  0220 (a) 16-28-35-47

• 

  0220 (b) 17-24-36-58

• 

  0301 (a) 12-36-47-58

• 

  0301 (b) 16-23-47-58

• 

  0400 (a) 14-27-36-58

• 

  0400 (b) 16-25-38-47

• 

  1012 (a) 12-35-48-67

• 

  1012 (b) 12-37-45-68

• 

  1111 (a) 16-28-37-45

• 

  1111 (b) 13-25-48-67

• 

  1111 (x) 12-36-48-57

• 

  1111 (y) 12-37-46-58

• 

  1210 (a) 13-26-47-58

• 

  1210 (b) 15-28-36-47

• 

  2002 (a) 12-37-48-56

• 

  2002 (b) 18-26-37-45

• 

  2020 (a) 13-26-48-57

• 

  2020 (b) 15-28-37-46

• 

  2200 (a) 16-25-37-48

• 

  2200 (b) 15-27-36-48

• 

  4000 15-26-37-48

Inskrivna relationer

0400 (a), inskrivet 0400 (b)

1111 (x), inskriven 1111 (a)

I vissa fall kan paren (a) och (b) [eller (a) och (x)] återställas genom att skriva in en kvadrat på liknande sätt. I andra fall är uppsättningarna [(a) & (b)] eller [(x) & (y)] spegelbildspar.

Generalisering till vanliga polygoner

För det allmänna fallet där brickorna är n -sidiga regelbundna polygoner med m ingångspunkter per sida så att produkten av $A(n) ,m)$ och m är jämn, kan antalet distinkta kombinationer beräknas som .

$A(n,m)={\frac {1}{n}}\cdot \ summa _{n=pq}\varphi (p)\cdot \alpha (p,mq)$

$\varphi (p)$ är Eulers totientfunktion , där $\varphi (p)=r\prod _{p \mid r}\left(1-{\frac {1}{p}}\right)$

$\alpha (p,mq)$ är en villkorlig funktion definierad som:

$\ alfa (p,mq)={\begin{cases}\sum _{0\leq 2j\leq mq}p^{j}{\dbinom {mq}{2j}}(2j-1)&{\text{ om }}p{\text{ är jämnt}}\\p^{\frac {mq}{2}}(mq-1)&{\text{om }}p{\text{ är udda}}\end {fall}}$

Till exempel har en 10-sidig dekagon med en enda bana per sida (5 banor totalt) 105 kombinationer.

Antal unika brickor med n sidor, var och en med m ingångspunkter

		m Ingångspunkter per sida
		0	1	2	3	4	5	6	7	8
n Antal sidor	0 (cirkel)	1		1		2		5		18
	1 (monogon)	1		1		3		15		105
	2 (digon)	1	1	3	11	65	513	5363	68219	N/C
	3 (triangel)	1		7		3483		N/C		N/C
	4 (fyrkantig)	1	2	35	2688	508277	N/C	N/C	N/C	N/C
	5 (femhörning)	1		193		N/C		N/C		N/C
	6 (hexagon)	1	5	1799	N/C	N/C	N/C	N/C	N/C	N/C
	7 (heptagon)	1		19311		N/C		N/C		N/C
	8 (oktagon)	1	18	254143	N/C	N/C	N/C	N/C	N/C	N/C
	9 (nonagon)	1		N/C		N/C		N/C		N/C
	10 (dekagon)	1	105	N/C	N/C	N/C	N/C	N/C	N/C	N/C

(Många av värdena från den ursprungliga källan är N/C, alltså inte beräknade)

Variationer

Spel med Serpentiles

namn	År	Banans färger		Kakelmaterial		Antal brickor	Anteckningar
Psyche-Paths	1969	3		Kartong		85 + 6 blank
Kaliko	tidigt 1980-tal	3		Lucite	(klar)	85	Lucitebitar fram till 2001. Nuvarande tryck använder bambu/träplattor.
				Trä
Tantrix	1988	4		Plast		56	Upp till tre färger visas på en enda bricka. Brickor är numrerade på baksidan. Triple Cross-plattor används inte.

Psyche-Paths

Ett spel Psyche-Paths kräver en till sex spelare. Spelare turas om att lägga brickor. Varje bricka som läggs bredvid plattor som redan har lagts måste fortsätta med färgen på banan/banorna på den/de befintliga intilliggande kanten/kanterna. Sex tomma brickor tillhandahålls som "jokerkort" och anses fortsätta på vilken intilliggande väg som helst. En bricka dras i början av spelet och placeras i mitten av spelplanen för att "seed" spelet.

I "Beginner" Psyche-Paths drar spelarna en bricka från en pool med framsidan nedåt när det är deras tur. En poäng ges för varje ansluten väg. Om spelaren inte kan spela brickan eller gör ett olagligt spel, behålls den och spelaren straffas med ett antal poäng lika med antalet vägar som går genom den behållna brickan i slutet av spelet.

I "Standard" Psyche-Paths drar två till fyra spelare varsin hand med sex brickor i början av spelet. Under varje tur kan spelare spela någon eller alla sina brickor, fylla på till en hand med sex brickor i slutet av sin tur från poolen med framsidan nedåt. När du lägger ner brickor delas poäng endast ut när två eller flera ändar av en befintlig väg är sammankopplade. Spelaren får ett antal poäng lika med antalet brickor som innehåller den anslutna färgbanan. Tre poäng delas ut om banan korsar sig själv, och poängen fördubblas om banan är stängd. Ingen påföljd tas för överblivna brickor. "Classic" Psyche-Paths liknar "Standard", men lägger till en regel att varje drag måste resultera i en enda väg genom alla brickor i det draget.

"Solitaire" Psyche-Paths har inga specifika regler, utan snarare förslag, som att bygga omväxlande rader med åtta och nio bitar långa med hjälp av lagliga drag.

Andra spel som använder vanliga polygonal brickor

Fyrkantiga brickor används i anslutningsspel som Black Path Game (med en enfärgad bana) och Trax (med tvåfärgade banor). Åttakantiga brickor med en enda banfärg används med mellanrum och en spelplan med förtryckta länkar för spelet Octiles .

Spelet Serpentiles (2008) utvecklades av Brett J. Gilbert och publicerades av ThinkFun 2008. Spelet Serpentiles (2008) innehåller 19 plastbrickor: 4 kvadratiska (1×1) och 12 rektangulära (2×1) brickor med en tryckt grön eller blå bana på vardera, och 3 kvadratiska (1×1) nodbrickor med sammanfallande blå och gröna bana ändar. 2008 års spel innehåller också 40 utmaningskort som ger en lista över brickor (inklusive två av noderna) som ska arrangeras så att en sammanhängande bana av varje färg skapas.

Historia

Det ursprungliga hex-kakel kantmatchande anslutningsspelet, Psyche-Paths, designades av Charles Titus och Craige Schensted och publicerades på 1960-talet med de 85 unika brickkombinationerna och 6 tomma "wild cards" på kartongbrickor. I en recension noterade forskare att spelet "rymmer en mängd olika åldrar, intressen och spelstilar ... [involverar] ett antal färdigheter som är av speciellt intresse för lärare och föräldrar." Steve Titus, son till Charles, återutgav spelet på 1980-talet som Kaliko med hjälp av screentryckta akrylplattor under familjeföretaget Future Games. Kaliko licensierades till Kadon 1986 med en övergång till träplattor efter 2001.

Tantrix släpptes 1988 av uppfinnaren Mike McManaway med hjälp av fyra av de fem möjliga vägkombinationerna (med Van Ness notation: 003 , 021 , 102 och 120 , exklusive 300 ) för att skapa 56 unika brickor, var och en med tre olika färger valda från en palett av fyra. Den primära innovationen med Tantrix är kodningen av siffror på baksidan av brickorna, vilket gör att delmängder av 56 kan användas för ensamma pussel.

Hex kakel set

Den kompletta uppsättningen med 85 brickor, förutsatt en kombination av upp till tre distinkta banfärger per ruta, visas i tabellen nedan, organiserad efter notation och antal färger.

003 aka Triple Bend
En färg	Två färger									Tre färger
021 aka Single Cross eller Cross Bend
En färg	Två färger									Tre färger
102 aka Double Bend
En färg	Två färger									Tre färger
120 aka Double Cross
En färg	Två färger									Tre färger
300 aka Triple Cross
En färg	Två färger									Tre färger

Tantrix använder enbart delmängden av brickor med tre olika banfärger och utesluter 300 Triple Cross-serien. Med fyra möjliga banfärger i Tantrix finns det fyra olika färgkombinationer med tre olika banfärger, vilket ger 56 unika Tantrix-brickor i en komplett uppsättning:

• 003 : 2 brickor med 3 banfärger × 4 banfärgskombinationer = 8 Tantrix brickor i set 003
• 021 : 6 brickor med 3 banfärger × 4 banfärgskombinationer = 24 Tantrix brickor i set 021
• 102 : 3 brickor med 3 banfärger × 4 banfärgskombinationer = 12 Tantrix brickor i set 102
• 120 : 3 brickor med 3 banfärger × 4 banfärgskombinationer = 12 Tantrix brickor i set 120

Tantrix kakel

Klass/uppsättning	stigar							stigar							stigar							stigar
003	#14			#03				#21			#23				#25			#28				#43			#45
021	#01		#11		#08			#17		#19		#31			#29		#37		#41			#53		#55		#46
	#10		#12		#07			#18		#20		#33			#27		#38		#36			#54		#56		#52
102	#02		#13		#05			#22		#16		#15			#26		#30		#24			#49		#47		#48
120	#06		#09		#04			#35		#34		#32			#42		#40		#39			#44		#50		#51

externa länkar

• Scherphuis, Jaap (2015). "Jaaps pusselsida: Tantrix" . jaapsch.net . Hämtad 8 oktober 2017 .