Satellitnavigeringslösning

Satellitnavigeringslösning för mottagarens position ( geopositionering ) involverar en algoritm. I huvudsak mäter en GNSS- mottagare sändningstiden för GNSS-signaler som sänds ut från fyra eller flera GNSS-satelliter (som ger pseudointervallet ) och dessa mätningar används för att erhålla dess position (dvs. rumsliga koordinater ) och mottagningstid.

Beräkningssteg

En global-navigation-satellite-system (GNSS)-mottagare mäter den skenbara sändningstiden, ${\displaystyle \displaystyle {\tilde {t}}_{i}},$ eller "fas", för GNSS-signaler som sänds ut från fyra eller fler GNSS- satelliter ( $\displaystyle i\;=\;1,\,2,\,3,\,4,\,..,\ ,n$ ), samtidigt.
GNSS-satelliter sänder meddelanden från satelliternas efemeris , $\displaystyle {\boldsymbol {r}}_{i}(t)$ och inre klockförspänning (dvs. klockförskjutning), ${\displaystyle \displaystyle \delta t_{{\text{klocka,sv}},i}(t)} [$ ^{förtydligande behövs ]} som funktionerna för ( atomär ) standardtid , t.ex. GPST .
Sändningstiden för GNSS-satellitsignaler, $\displaystyle t_{i}$ , härleds alltså från ekvationerna i icke -sluten form ${\ displaystyle \displaystyle {\tilde {t}}_{i}\;=\;t_{i}\,+\,\delta t_{{\text{clock}},i}(t_{i})}$ och ${\displaystyle \displaystyle \delta t_{{\text{ klocka}},i}(t_{i})\;=\;\delta t_{{\text{klocka,sv}},i}(t_{i})\,+\,\delta t_{{\ text{orbit-relativ}},\,i}({\boldsymbol {r}}_{i},\,{\dot {\boldsymbol {r}}}_{i})} ,$ där $\displaystyle \delta t_{{\text{orbit-relativ}},i}({\boldsymbol {r}}_{i},\,{\dot {\boldsymbol {r}}}_{i})$ är den relativistiska klockförspänningen, periodiskt stigande från satellitens orbitala excentricitet och jordens gravitationsfält . Satellitens position och hastighet bestäms av $\displaystyle t_{i}$ enligt följande: $\displaystyle {\boldsymbol {r}}_{i}\; =\;{\boldsymbol {r}}_{i}(t_{i})$ och $\displaystyle {\dot {\boldsymbol {r}}}_ {i}\;=\;{\dot {\boldsymbol {r}}}_{i}(t_{i})$ .
I fältet för GNSS, "geometriskt område", $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B })$ , definieras som rakt avstånd, eller 3-dimensionellt avstånd , från $\displaystyle {\boldsymbol {r}}_{A}$ till $\displaystyle {\boldsymbol {r} }_{B}$ i tröghetsram (t.ex. jordcentrerad tröghet (ECI) ett), inte i roterande ram .
Mottagarens position, $\displaystyle {\boldsymbol {r}}_{\text{rec}}$ och mottagningstid, $\displaystyle t_{\text{rec}}$ , uppfyller ljuskonekvationen för $r}}_{\text{rec}})/c\,+\,(t_{i}-t_{\text{rec}})\;=\;0} i tröghetsram ,$ ${\displaystyle \displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol$ { där c { $displaystyle \displaystyle c}$ är ljusets hastighet . Signaltiden för flygning från satellit till mottagare är $\displaystyle -(t_{i}\,-\,t_{\text{rec}})$ .
Ovanstående utvidgas till positioneringsekvationen för satellitnavigering $displaystyle \displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}\,-\,t_ {\text{rec}})\,+\,\delta t_{{\text{atmos}},i}\,-\,\delta t_{{\text{meas-err}},i}\; =\;0}$ , \ , där $\displaystyle \delta t_{{\text{atmos}},i}$ är atmosfärisk fördröjning (= jonosfärisk fördröjning + troposfärisk fördröjning ) längs signalvägen och $\displaystyle \delta t_{{\text{meas-err}},i}$ är mätfelet.
Gauss –Newton -metoden kan användas för att lösa det olinjära minsta kvadrat-problemet för lösningen: ${\displaystyle \displaystyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})\;=\;\arg \min \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})} , där ϕ$ ( $\displaystyle \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})\;=\; \sum _{i=1}^{n}(\delta t_{{\text{meas-err}},i}/\sigma _{\delta t_{{\text{meas-err}},i} })^{2}$ . Observera att $\displaystyle \delta t_{{\text{meas-err}},i}$ ska betraktas som en funktion av $\displaystyle {\boldsymbol {r }}_{\text{rec}}$ och $\displaystyle t_{\text{rec}}$ .
Den bakre fördelningen av $\displaystyle {\boldsymbol {r}}_{\text{rec}}$ och $\displaystyle t_{\text{rec}}$ är proportionell mot $\displaystyle \exp(-{\frac {1}{2}}\phi ({\boldsymbol {r}}_{\text{rec}}, \,t_{\text{rec}}))$ , vars läge är $\displaystyle ({\hat {\boldsymbol {r}}}_{\text{rec} },\,{\hat {t}}_{\text{rec}})$ . Deras slutledning är formaliserad som en maximal uppskattning i efterhand .
Den bakre fördelningen av $\displaystyle {\boldsymbol {r}}_{\text{rec}}$ är proportionell mot $\displaystyle \int _{-\infty }^{\infty }\exp(-{\frac {1}{2}}\phi ({\boldsymbol {r}}_{\text{rec }},\,t_{\text{rec}}))\,dt_{\text{rec}}$ .

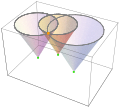
Lösningen illustrerad

I huvudsak är lösningen, $\scriptstyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_ {\text{rec}})$ , är skärningspunkten mellan ljuskoner .
Den bakre fördelningen av lösningen härleds från produkten av fördelningen av fortplantande sfäriska ytor. (Se animation .)

GPS-fodralet

För Global Positioning System (GPS) resulterar ekvationerna i icke-sluten form i steg 3 i

\scriptstyle {\begin{cases}\scriptstyle \Delta t_ {i}(t_{i},\,E_{i})\;\triangleq \;t_{i}\,+\,\delta t_{{\text{klocka}},i}(t_{i} ,\,E_{i})\,-\,{\tilde {t}}_{i}\;=\;0,\\\scriptstyle \Delta M_{i}(t_{i},\,E_ {i})\;\triangleq \;M_{i}(t_{i})\,-\,(E_{i}\,-\,e_{i}\sin E_{i})\;=\ ;0,\end{cases}}

där $\scriptstyle E_{i}$ är den excentriska orbitala anomin för satellit $i$ , $\scriptstyle M_{i}$ är medelanomali , $\scriptstyle e_{i}$ är excentriciteten och ${\ displaystyle \scriptstyle \delta t_{{\text{klocka}},i}(t_{i},\,E_{i})\;=\;\delta t_{{\text{klocka,sv}},i }(t_{i})\,+\,\delta t_{{\text{orbit-relativ}},i}(E_{i})}$ .

Ovanstående kan lösas genom att använda den bivariata Newton–Raphson -metoden på $\scriptstyle t_{i}$ och $\scriptstyle E_{i}$ . Två gångers iteration kommer att vara nödvändigt och tillräckligt i de flesta fall. Dess iterativa uppdatering kommer att beskrivas genom att använda den ungefärliga inversen av jakobiansk matris enligt följande:

$\scriptstyle {\begin{pmatrix}t_{i}\\E_{i}\\\end{pmatrix}}\leftarrow {\begin{pmatrix}t_{i}\\E_{i}\\\ end{pmatrix}}-{\begin{pmatrix}1&&0\\{\frac {{\dot {M}}_{i}(t_{i})}{1-e_{i}\cos E_{i} }}&&-{\frac {1}{1-e_{i}\cos E_{i}}}\\\end{pmatrix}}{\begin{pmatrix}\Delta t_{i}\\\Delta M_ {i}\\\end{pmatrix}}$

Troposfärisk fördröjning bör inte ignoreras, medan specifikationen för Global Positioning System (GPS) inte ger sin detaljerade beskrivning.

GLONASS-fallet

GLONASS- ephemeriderna ger inte klockförändringar ${\displaystyle \scriptstyle \delta t_{{\text{clock,sv}},i}(t)} ,$ utan $\scriptstyle \delta t_{{\text{klocka}},i}(t)$ .

Se även

Dags att fixa först

Anteckningar

I fältet GNSS, ${\displaystyle \scriptstyle {\tilde {r}}_{i}\;=\;-c({\tilde {t }}_{i}\,-\,{\tilde {t}}_{\text{rec}})} kallas pseudorange , där t ~ rec {\displaystyle$ \ scriptstyle { $t}}_{ \text{rec}}}$ är en provisorisk mottagningstid för mottagaren. $\scriptstyle \delta t_{\text{clock,rec}}\;=\;{\tilde {t}}_{\text{rec}}\ ,-\,t_{\text{rec}}$ kallas mottagarens klockförspänning (dvs. klockförskjutning).
Standard GNSS-mottagare utmatar $\scriptstyle {\tilde {r}}_{i}$ och $\scriptstyle {\tilde {t}}_{\text{rec}}$ per en observationsepok .
Den tidsmässiga variationen i satellitens relativistiska klockförspänning är linjär om dess bana är cirkulär (och därmed dess hastighet är enhetlig i tröghetsramen).
Signaltiden för flygning från satellit till mottagare uttrycks som $\scriptstyle -(t_{i}- t_{\text{rec}})\;=\;{\tilde {r}}_{i}/c\,+\,\delta t_{{\text{klocka}},i}\,-\ ,\delta t_{\text{clock,rec}}$ , vars högra sida är avrundningsfelresistiv under beräkning.
Det geometriska området beräknas som $\scriptstyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})\;=\;|\Omega _{\text{ E}}(t_{i}\,-\,t_{\text{rec}}){\boldsymbol {r}}_{i,{\text{ECEF}}}\,-\,{\boldsymbol { r}}_{\text{rec,ECEF}}|$ , där den jordcentrerade, jordfixerade (ECEF) roterande ramen (t.ex. WGS84 eller ITRF ) används på höger sida och $\ scriptstyle \Omega _{\text{E}}$ är jordens roterande matris med argumentet för signalens transittid . Matrisen kan faktoriseras som $\scriptstyle \Omega _{ \text{E}}(t_{i}\,-\,t_{\text{rec}})\;=\;\Omega _{\text{E}}(\delta t_{\text{klocka, rec}})\Omega _{\text{E}}(-{\tilde {r}}_{i}/c\,-\,\delta t_{{\text{clock}},i})$ .
Synlinjeenhetsvektorn för satellit observerad vid $\scriptstyle {\boldsymbol {r}}_{\text{rec,ECEF}}$ beskrivs som: $\scriptstyle {\boldsymbol {e}}_{i,{\text{rec,ECEF}}}\;=\;-{\frac {\partial r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})}{\partial {\boldsymbol {r}}_{\text {rec,ECEF}}}}$ .
Satellitnavigationspositioneringsekvationen kan uttryckas genom att använda variablerna $\scriptstyle {\boldsymbol {r}}_{\text{rec,ECEF}}$ och δ t clock $\displaystyle \ skriptstil \delta t_{\text{clock,rec}}}$ .
Icke-linjäriteten hos det vertikala beroendet av troposfärsfördröjning försämrar konvergenseffektiviteten i Gauss-Newton- iterationerna i steg 7.
Ovanstående notation skiljer sig från den i Wikipedia-artiklarna, 'Positionsberäkningsintroduktion' och 'Positionsberäkning avancerad', i Global Positioning System (GPS).

Se även

^ ^a ^b Misra, P. och Enge, P., Global Positioning System: Signaler, mätningar och prestanda, 2nd, Ganga-Jamuna Press, 2006.
^ ^a ^b ^c ^d ^e ^f Gränssnittsspecifikationen för NAVSTAR GLOBAL POSITIONING SYSTEM
^ 3-dimensionellt avstånd ges av $\displaystyle r({\boldsymbol {r}}_{A},\,{\ fetsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B })^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ där $\displaystyle {\boldsymbol {r}}_{A}=(x_{A},y_{A},z_{A})$ och ${\displaystyle \displaystyle {\boldsymbol {r}}_{B}=(x_{B},y_{B},z_{B})} representerad$ i tröghetsram .

externa länkar

PVT (Position, Velocity, Time): Beräkningsprocedur i GNSS-SDR med öppen källkod och den underliggande RTKLIB

[Misra_Enge-1] Misra, P. och Enge, P., Global Positioning System: Signaler, mätningar och prestanda, 2nd, Ganga-Jamuna Press, 2006.

[IS-GPS-2] ^ ^a ^b ^c ^d ^e ^f Gränssnittsspecifikationen för NAVSTAR GLOBAL POSITIONING SYSTEM

[3] 3-dimensionellt avstånd ges av $\displaystyle r({\boldsymbol {r}}_{A},\,{\ fetsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B })^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ där $\displaystyle {\boldsymbol {r}}_{A}=(x_{A},y_{A},z_{A})$ och ${\displaystyle \displaystyle {\boldsymbol {r}}_{B}=(x_{B},y_{B},z_{B})} representerad$ i tröghetsram .