Rytz konstruktion

Rytz konstruktion: start - slut

Rytz -axelkonstruktionen är en grundläggande metod för beskrivande geometri för att hitta axlarna, halvstoraxeln och semi-mollaxeln och hörnen på en ellips , med utgångspunkt från två konjugerade halvdiametrar . Om centrum och halvaxeln för en ellips bestäms kan ellipsen ritas med hjälp av en ellipsografi eller för hand (se ellips ).

Rytz konstruktion är en klassisk konstruktion av euklidisk geometri , där endast kompass och linjal är tillåtna som hjälpmedel. Designen är uppkallad efter dess uppfinnare David Rytz från Brugg (1801–1868).

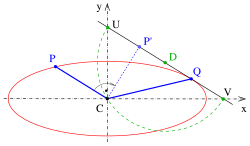
Konjugerade diametrar visas alltid om en cirkel eller en ellips projiceras parallellt (strålarna är parallella) som bilder av ortogonala diametrar på en cirkel (se andra diagrammet) eller som bilder av en ellips axlar. En väsentlig egenskap hos två konjugerade diametrar $d_{1},\;d_{2}$ är: Tangenterna vid ellipspunkterna för en diameter är parallella med den andra diametern (se andra diagrammet).

Kub med cirklar: militär projektion

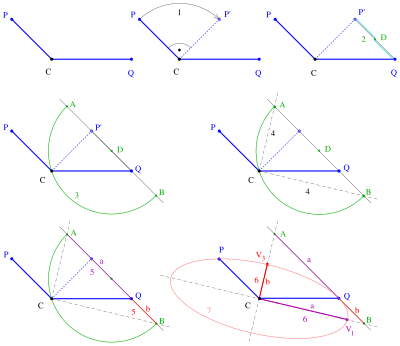
Rytz konstruktion i 6 steg. Givet: centrum C och två konjugerade halvdiametrar CP, CQ av en ellips. sökte: halvaxlarna och ellipsens hörn.

Problembeskrivning och lösning

Den parallella projektionen (skev eller ortografisk) av en cirkel som i allmänhet är en ellips (det speciella fallet med ett linjesegment som bild utelämnas). En grundläggande uppgift inom beskrivande geometri är att rita en sådan bild av en cirkel. Diagrammet visar en militär projektion av en kub med 3 cirklar på 3 ytor av kuben. Bildplanet för en militär projektion är horisontellt. Det betyder att cirkeln på toppen visas i sin verkliga form (som cirkel). Bilderna av cirklarna vid de andra två ansiktena är uppenbarligen ellipser med okända yxor. Men man känner i alla fall igen bilderna av två ortogonala diametrar på cirklarna. Dessa diametrar på ellipserna är inte längre ortogonala men som bilder av ortogonala diametrar på cirkeln är de konjugerade (tangenserna vid ändpunkterna för en diameter är parallella med den andra diametern !). Detta är en standardsituation i beskrivande geometri:

• Från en ellips är mitten $C$ och två punkter $P,Q$ på två konjugatdiametrar kända.
• Uppgift: hitta ellipsens axlar och halvaxlar.

Steg av konstruktionen

(1) rotera punkt $P$ runt $C$ med 90°. (2) Bestäm mitten $D$ för linjesegmentet ${\overline {P'Q}}$ . (3) Rita linjen $P'Q$ och cirkeln med centrum $D$ till $C$ . Skär cirkeln och linjen. Skärningspunkterna är $A,B$ . (4) Linjerna $CA$ och $CB$ är ellipsens axlar . (5) Linjesegmentet ${\overline {AB}}$ kan betraktas som en pappersremsa med längden $a+b$ (se ellips ) genererande punkt $Q$ . Därför $a=|AQ|$ och $b=|BQ|$ är halvaxlarna . (Om $a>b$ så är $a$ semi- storaxeln .) (6) Hörnen och medhörnen är kända och ellipsen kan ritas med någon av ritmetoderna .

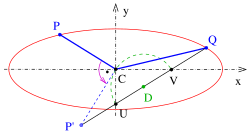
Om man utför en vänstersväng av punkt $P$ visar konfigurationen den andra pappersremsmetoden (se andra diagrammet i nästa avsnitt) och $a=|AQ|$ och $b=|BQ|$ är fortfarande sant.

Bevis på uttalandet

Rytz: bevis

Standardprovet utförs geometriskt. Ett alternativt bevis använder analytisk geometri:

Beviset är gjort, om man kan visa det

• skärningspunkterna $U,V$ för linjen $P'Q$ med ellipsens axlar ligger på cirkeln genom $C$ med centrum $D$ , därav $U=A$ och $V=B$ , och $|UQ|=a,\quad |VQ|=b\ .$

Bevis

(1): Vilken ellips som helst kan representeras i ett lämpligt koordinatsystem parametriskt med

${\vec {p}}(t)=(a\cos t,\;b\sin t)^{T}$ .

Två punkter ${\vec {p}}(t_{1}),\ {\vec {p}}(t_{2})$ ligger på konjugat diametrar om $t_{2}-t_{1}=\pm {\tfrac {\pi }{2}}\ .$ (se Ellips: konjugerade diametrar .)

(2): Låt vara $Q=(a\cos t,\;b\sin t)$ och

${\displaystyle P=(a\cos(t+{\tfrac {\pi }{2}}),\;b\sin(t+{\tfrac {\pi }{2}}))=(-a\sin t,b\cos t)} två punkter på konjugerade diametrar$

.

Då $P'=(b\cos t,a\sin t)$ och mittpunkten av linjesegmentet ${\overline { P'Q}}$ är $D=\left({\tfrac {a+b}{2}}\cos t, {\tfrac {a+b}{2}}\sin t\right)$ .

(3): Linje $P'Q$ har ekvationen $x\sin t+y\cos t=(a+b)\;\cos t\sin t\ .$

Skärningspunkterna för denna linje med ellipsens axlar är

$U=\left(0,\;(a+b)\sin t\right)\ ,\quad V=\left((a+b)\cos t,\;0\right)\ .$

Rytz: vänstersväng av punkt $P$

(4): På grund av $|UD|=|VD|=|CD|$ punkterna $U,V,C$ ligger på cirkeln med centrum $D$ och radie $|CD|\ .$

Därför $A=U,\ B=V\ .$

(5): $|UQ|=a,\quad |VQ|=b\ .$

Beviset använder en högersväng av punkten $P$ , vilket leder till ett diagram som visar den första pappersremsmetoden .

Variationer

Om man utför en vänstersväng av punkten $P$ är resultaten (4) och (5) fortfarande giltiga och konfigurationen visar nu den andra pappersremsmetoden (se diagram). Om man använder $P=(a\cos(t {\color {röd}-}{\tfrac {\pi }{2}}),\;b\sin(t{\color {röd}-}{\tfrac {\pi }{2}}))= (a\sin t,-b\cos t)$ , då fungerar konstruktionen och bevisningen heller.

Datorstödd lösning

För att hitta ellipsens hörn med hjälp av en dator,

• koordinaterna för de tre punkterna $C,P,Q$ måste vara kända.

En enkel idé är: Man kan skriva ett program som utför de steg som beskrivs ovan. En bättre idé är att använda representationen av en godtycklig ellips parametriskt:

• ${\vec {x}}={\vec {p}}(t)={\vec {f}}_{0}+{\vec {f}}_{1}\cos t+{\ vec {f}}_{2}\sin t\ .$

Med ${\vec {f}}_{0}={\vec {OC}}$ (mitten) och ${\displaystyle {\vec {f}}_{1}={\vec {CP}},\;{\vec {f}}_{2}={\vec {CQ}}} (två konjugat$ halv- diametrar) kan man beräkna poäng och rita ellipsen.

Vid behov: Med $\cot(2t_{0})={\tfrac {{\vec {f} }_{1}^{\,2}-{\vec {f}}_{2}^{\,2}}{2{\vec {f}}_{1}\cdot {\vec {f }}_{2}}}$ man får ellipsens fyra hörn: ${\vec {p}}(t_{0}),\;{\vec {p}}(t_{0}\pm {\frac {\pi}{2}}),\;{\ vec {p}}(t_{0}+\pi )\ .$

•   Rudolf Fucke; Konrad Kirch; Heinz Nickel (2007). Darstellende Geometrie für Ingenieure [ Beskrivande geometri för ingenjörer ] (på tyska) (17:e upplagan). München: Carl Hanser. sid. 183. ISBN 978-3446411432 . Hämtad 2013-05-31 .
•   Klaus Ulshöfer; Dietrich Tilp (2010). "5: Ellipse als ortogonal-affines Bild des Hauptkreises " [5: "Ellips som den ortogonala affina bilden av enhetscirkeln"]. Darstellende Geometrie in systematischen Beispielen [ Beskrivande geometri i systematisk samling av exempel ]. Übungen für die gymnasiale Oberstufe (på tyska) (1:a upplagan). Bamberg: CC Buchner. ISBN 978-3-7661-6092-8 .
•   Alexander Ostermann; Gerhard Wanner (2012). Geometri genom dess historia . Springer Science & Business Media. s. 68–69. ISBN 9783642291630 .

externa länkar

• animering av Rytz konstruktion