Rombergs metod

I numerisk analys används Rombergs metod för att uppskatta den bestämda integralen

\int _{a}^{b}f(x)\,dx

genom att tillämpa Richardson-extrapolation upprepade gånger på trapetsregeln eller rektangelregeln (mittpunktsregeln). Uppskattningarna genererar en triangulär array . Rombergs metod är en Newton-Cotes-formel – den utvärderar integranden vid punkter med lika mellanrum. Integranden måste ha kontinuerliga derivat, även om ganska bra resultat kan erhållas om bara ett fåtal derivat finns. Om det är möjligt att utvärdera integranden vid ojämnt fördelade punkter, är andra metoder som Gaussisk kvadratur och Clenshaw–Curtis kvadratur i allmänhet mer exakta.

Metoden är uppkallad efter Werner Romberg (1909–2003), som publicerade metoden 1955.

Metod

Med hjälp av ${\textstyle h_{n}={\frac {(ba)}{2^{n}}}} ,$ kan metoden definieras induktivt av

{\begin{aligned}R(0,0)&=h_{1}( f(a)+f(b))\\R(n,0)&={\tfrac {1}{2}}R(n-1,0)+h_{n}\summa _{k=1 }^{2^{n-1}}f(a+(2k-1)h_{n})\\R(n,m)&=R(n,m-1)+{\tfrac {1}{ 4^{m}-1}}(R(n,m-1)-R(n-1,m-1))\\&={\frac {1}{4^{m}-1}} (4^{m}R(n,m-1)-R(n-1,m-1))\end{aligned}}

där

n\geq m

och

m\geq 1\,

. I stor O-notation är felet för R ( n , m ):

O\left(h_{n}^{2m+2}\right).

Nollpunktsextrapoleringen, $R (n, 0 )$ , är ekvivalent med trapetsregeln med $2 n + 1$ poäng; den första extrapoleringen, $R (n, 1 )$ , motsvarar Simpsons regel med $2 n + 1$ poäng. Den andra extrapoleringen, $R (n, 2)$ , motsvarar Booles regel med $2 n + 1$ poäng. De ytterligare extrapoleringarna skiljer sig från Newton-Cotes formler. I synnerhet ytterligare Romberg-extrapolationer expanderar på Booles regel på mycket små sätt, och modifierar vikter till förhållanden liknande Booles regel. Däremot producerar ytterligare Newton-Cotes-metoder allt mer olika vikter, vilket så småningom leder till stora positiva och negativa vikter. Detta är en indikation på hur stor grad interpolerande polynom Newton-Cotes-metoder misslyckas med att konvergera för många integraler, medan Romberg-integration är mer stabil.

Genom att märka våra ${\textstyle O(h^{2})}$ approximationer som ${\textstyle A_{0}{\big (}{\frac {h}{2^{ n}}}{\big )}}$ istället för ${\textstyle R(n,0)}$ , kan vi utföra Richardson-extrapolering med felformeln som definieras nedan:

\int _ {a}^{b}f(x)\,dx=A_{0}{\bigg (}{\frac {h}{2^{n}}}{\bigg )}+a_{0}{\ bigg (}{\frac {h}{2^{n}}}{\bigg )}^{2}+a_{1}{\bigg (}{\frac {h}{2^{n}}} {\bigg )}^{4}+a_{2}{\bigg (}{\frac {h}{2^{n}}}{\bigg )}^{6}+\cdots

När vi har fått våra

{\textstyle O(h^{2(m+1)})}

approximationer

{\textstyle A_{m}{\big (}{\frac {h}{2^{n}}}{\big )}}

, vi kan märka dem som

{\textstyle R(n,m)}

.

När funktionsutvärderingar är dyra kan det vara att föredra att ersätta polynominterpolationen av Richardson med den rationella interpolationen som föreslås av Bulirsch & Stoer (1967) .

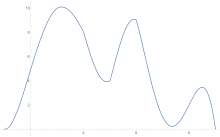
Ett geometriskt exempel

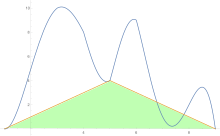
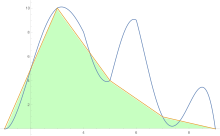
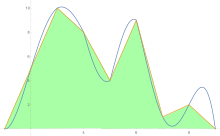
För att uppskatta arean under en kurva tillämpas trapetsregeln först på ett stycke, sedan två, sedan fyra, och så vidare.

En bit. Observera att eftersom det börjar och slutar på noll, ger denna approximation noll area.

Tvådelad

Fyra delar

Åtta delar

Efter att trapetsregeluppskattningar har erhållits, tillämpas Richardson-extrapolering .

För den första iterationen används tvådelade och endelade uppskattningar i formeln (4 × (mer exakt) − (mindre exakt))/3 Samma formel används sedan för att jämföra uppskattningen av fyra delar och tvådelad uppskattning, och likaså för de högre uppskattningarna
För den andra iterationen används värdena för den första iterationen i formeln ( 16(mer exakt) − mindre exakt))/15
Den tredje iterationen använder nästa potens av 4: (64 (mer exakt) − mindre korrekt))/63 på värdena som härleds av den andra iterationen.
Mönstret fortsätter tills det finns en uppskattning.

Antal bitar	Trapetsuppskattningar	Första iterationen	Andra iterationen	Tredje iterationen
		(4 MA − LA)/3*	(16 MA − LA)/15	(64 MA − LA)/63
1	0	(4×16 − 0)/3 = 21,333...	(16×34,667 − 21,333)/15 = 35,556...	(64×42.489 − 35.556)/63 = 42.599...
2	16	(4×30 − 16)/3 = 34,666...	(16×42 − 34,667)/15 = 42,489...
4	30	(4×39 − 30)/3 = 42
8	39

MA står för mer exakt, LA står för mindre exakt

Exempel

Som ett exempel är Gauss-funktionen integrerad från 0 till 1, dvs felfunktionen erf(1) ≈ 0,842700792949715. Den triangulära matrisen beräknas rad för rad och beräkningen avslutas om de två sista posterna i den sista raden skiljer sig mindre än 10 ⁻⁸ .

0,77174333 0,82526296 0,84310283 0,83836778 0,84273605 0,84271160 0,84161922 0,84270304 0,83420604 0,834206040.504 0,84270093 0,84270079 0,84270079 0,84270079

Resultatet i det nedre högra hörnet av den triangulära matrisen stämmer överens med de visade siffrorna. Det är anmärkningsvärt att detta resultat härrör från de mindre exakta approximationerna som erhålls av trapetsregeln i den första kolumnen i den triangulära arrayen.

Genomförande

Här är ett exempel på en datorimplementering av Romberg-metoden (i programmeringsspråket C ):

 
 

     
    
       0     
       
   
   













           

      
      0   0 
       
   0     

   0 

            
        
         0
            
               
           
      
      0    0 

               
             
                
      

      
       

              
          
      

      
         
        
        
   
     
 #include  <stdio.h>  #include  <math.h>  void  print_row  (  size_t  i  ,  double  *  R  )  {  printf  (  "R[%2zu] = "  ,  i  );  för  (  storlek_t  j  =  ;  j  <=  i  ;  ++  j  )  {  printf  (  "%f"  ,  R  [  j  ]);  }  printf  (  "  \n  "  );  }  /*  INPUT:  (*f) : pekare till funktionen som ska integreras  a : nedre gräns  b : övre gräns  max_steps: maximala steg i proceduren  acc : önskad noggrannhet  OUTPUT:  Rp[max_steps-1]: ungefärligt värde för integralen av funktionen f för x i [a,b] med noggrannheten 'acc' och stegen 'max_steps'.  */  dubbel  romberg  (  dubbel  (  *  f  )(  dubbel  ),  dubbel  a  ,  dubbel  b  ,  storlek_t  max_steg  ,  dubbel  acc  )  {  dubbel  R1  [  max_steg  ],  R2  [  max_steg  ];  // buffertar  dubbel  *  Rp  =  &  R1  [  ],  *  Rc  =  &  R2  [  ];  // Rp är föregående rad, Rc är nuvarande rad  dubbel  h  =  b  -  a  ;  //stegstorlek  Rp  [  ]  =  (  f  (  a  )  +  f  (  b  ))  *  h  *  0,5  ;  // första trapetsformade steg  print_row  (  ,  Rp  );  för  (  storlek_t  i  =  1  ;  i  <  max_steg  ;  ++  i  )  {  h  /=  2.  ;  dubbel  c  =  ;  size_t  ep  =  1  <<  (  i  -1  );  //2^(n-1)  för  (  storlek_t  j  =  1  ;  j  <=  ep  ;  ++  j  )  {  c  +=  f  (  a  +  (  2  *  j  -1  )  *  h  );  }  Rc  [  ]  =  h  *  c  +  .5  *  Rp  [  ];  // R(i,0)  för  (  storlek_t  j  =  1  ;  j  <=  i  ;  ++  j  )  {  dubbel  n_k  =  pow  (  4  ,  j  );  Rc  [  j  ]  =  (  n_k  *  Rc  [  j  -1  ]  -Rp  [  j  -1  ])  /  (  n_k  -  1  );  // beräkna R(i,j)  }  // Skriv ut raden av R, R[i,i] är den bästa uppskattningen hittills  print_row  (  i  ,  Rc  );  if  (  i  >  1  &&  fabs  (  Rp  [  i  -1  ]  -  Rc  [  i  ])  <  acc  )  {  retur  Rc  [  i  ];  }  // byt Rn och Rc eftersom vi bara behöver den sista raden  dubbel  *  rt  =  Rp  ;  Rp  =  Rc  ;  Rc  =  rt  ;  }  returnera  Rp  [  max_steg  -1  ];  // returnera vår bästa gissning  }

Här är ett exempel på en datorimplementering av Romberg-metoden i programmeringsspråket Javascript .












       
       
      
  
       
      
  
      
      
  
          0 
      
  
          0 
      
  
    
       
  
      
      0     
    
        0     
      0
    
  

  
  00      
     00

       
    
    
    
	    
       0
         
       
    

    0  0  
    
    
           
       
      
        

      
         
      
           
			
      
        

      
          
         
      
    
  
  
   
 /**  * INPUT  * func = integrand, funktion som ska integreras  * a = nedre gräns för integration  * b = övre gräns för integration  * nmax = antal partitioner, n=2^nmax  * tol_ae = maximalt absolut ungefärligt fel acceptabelt (bör vara >=0)  * tol_rae = maximalt absolut relativ ungefärligt fel acceptabelt (bör vara >=0)  * OUTPUTS  * integ_value = uppskattat värde för integral  */  funktion  auto_integrator_trap_romb_hnm  (  func  ,  a  ,  b  ,  nmax  ,  tol_ae  ,  tol_rae  )  {  if  ( rae )   typeof  a  !==  'number'  )  {  throw  new  TypeError  (  '<a> måste vara ett nummer'  );  }  if  (  typeof  b  !==  'number'  )  {  throw  new  TypeError  (  '<b> måste vara ett nummer'  );  }  if  (  !  Number  .  isInteger  (  nmax  )  ||  nmax  <  1  )  {  throw  new  TypeError  (  '<nmax> måste vara ett heltal större än eller lika med ett.'  );  }  if  ((  typeof  tol_ae  !==  'number'  )  ||  tol_ae  <  )  {  throw  new  TypeError  (  '<tole_ae> måste vara ett tal större än eller lika med noll' )  ;  }  if  ((  typeof  tol_rae  !==  'number'  )  ||  tol_rae  <=  )  {  throw  new  TypeError  (  '<tole_ae> måste vara ett tal större än eller lika med noll' )  ;  }  var  h  =  b  -  a  ;  // initiera matris där integralens värden lagras  var  Romb  =  [];  // rader  för  (  var  i  =  ;  i  <  nmax  +  1  ;  i  ++  )  {  Romb  .  tryck  ([]);  för  (  var  j  =  ;  j  <  nmax  +  1  ;  j  ++  )  {  Romb  [  i  ].  push  (  matte  .  stort nummer  (  ));  }  }  // beräknar värdet med 1-segments trapetsregel  Romb  [  ][  ]  =  0,5  *  h  *  (  func  (  a  )  +  func  (  b  ));  var  integ_val  =  Romb  [  ][  ];  for  (  var  i  =  1  ;  i  <=  nmax  ;  i  ++  )  {  // uppdatera värdet med dubbla antalet segment  // genom att endast använda de värden där de behöver beräknas  // Se https://autarkaw. org/2009/02/28/an-efficient-formula-for-an-automatic-integrator-based-on-trapezoidal-rule/  h  =  h  /  2  ;  var  integ  =  ;  för  (  var  j  =  1  ;  j  <=  2  **  i  -  1  ;  j  +=  2  )  {  var  integ  =  integ  +  func  (  a  +  j  *  h  )  }  Romb  [  i  ][  ]  =  0,5  *  Romb  [  i  -  1  ][  ]  +  integ  *  h  ;  // Använder Romberg-metoden för att beräkna nästa extrapolerbara värde  // Se https://young.physics.ucsc.edu/115/romberg.pdf  för  (  k  =  1  ;  k  <=  i  ;  k  ++  )  {  var  addterm  =  Romb  [  i  ][  k  -  1  ]  -  Romb  [  i  -  1  ][  k  -  1  ]  addterm  =  addterm  /  (  4  **  k  -  1.0  )  Romb  [  i  ][  k  ]  =  Romb  [  i  ][  k  -  1  ]  +  addterm  // Beräknar absolut ungefärligt fel  var  Ea  =  math  .  abs  (  Romb  [  i  ][  k  ]  -  Romb  [  i  ][  k  -  1  ])  // Beräknar absolut relativ ungefärligt fel  var  epsa  =  math  .  abs  (  Ea  /  Romb  [  i  ][  k  ])  *  100,0  ;  //Tilldelning av det senaste värdet till returvariabeln  integ_val  =  Romb  [  i  ][  k  ];  // returnerar värdet om någon av toleranserna är uppfyllda  if  (  epsa  <  tol_rae  ||  Ea  <  tol_ae  )  {  return  integ_val  ;  }  }  }  // returnerar det senast beräknade värdet av integralen oavsett om toleransen är uppfylld eller inte  returnerar  integ_val  ;  }

Richardson, LF (1911), "The Approximate Arithmetical Solution by Finite Differences of Physical Problems Involving Differential Equations, with an Application to the Stresses in a Masonry Dam", Philosophical Transactions of the Royal Society A , 210 (459–470): 307 –357, doi : 10.1098/rsta.1911.0009 , JSTOR 90994
Romberg, W. (1955), "Vereinfachte numerische Integration", Det Kongelige Norske Videnskabers Selskab Forhandlinger , Trondheim, 28 (7): 30–36
Thacher Jr., Henry C. (juli 1964), "Remark on Algorithm 60: Romberg integration" , Communications of the ACM , 7 (7): 420–421, doi : 10.1145/364520.364542
Bauer, FL; Rutishauser, H.; Stiefel, E. (1963), Metropolis, NC; et al. (red.), "New aspects in numerical quadrature", Experimental Arithmetic, high-speed computing and mathematics, Proceedings of Symposia in Applied Mathematics , AMS (15): 199–218
Bulirsch, Roland; Stoer, Josef (1967), "Handbook Series Numerical Integration. Numerical quadrature by extrapolation" , Numerische Mathematik , 9 : 271–278, doi : 10.1007/bf02162420
Mysovskikh, IP (2002) [1994], "Romberg-metoden" , i Hazewinkel, Michiel (red.), Encyclopedia of Mathematics , Springer-Verlag , ISBN 1-4020-0609-8
Tryck, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Avsnitt 4.3. Romberg Integration" , Numeriska recept: The Art of Scientific Computing (3:e upplagan), New York: Cambridge University Press, ISBN 978-0-521-88068-8

externa länkar

ROMBINT – kod för MATLAB (författare: Martin Kacenak)
Gratis onlineintegreringsverktyg med Romberg, Fox–Romberg, Gauss–Legendre och andra numeriska metoder
SciPy implementering av Rombergs metod
Romberg.jl — Julia- implementering (stöder godtyckliga faktoriseringar, inte bara $2^{n}+1$ poäng)