Rektangulär mask korttids Fouriertransform

Inom matematik och Fourieranalys har en rektangulär mask korttids Fouriertransform (rec-STFT) den enkla formen av korttids Fouriertransform . Andra typer av STFT kan kräva mer beräkningstid än rec-STFT.

Den rektangulära maskfunktionen kan definieras för någon gräns ( B) över tid ( t ) som

$w(t)={\begin{cases}\ 1;&|t|\leq B\\\ 0;&|t|>B\end{cases}}$

B = 50, x -axel (sek)

Vi kan ändra B för olika avvägningar mellan önskad tidsupplösning och frekvensupplösning.

Rec-STFT

$X(t,f)=\int _{tB}^{t+B}x (\tau )e^{-j2\pi f\tau }\,d\tau$

Omvänd form

$x(t)=\int _{-\infty }^{\infty }X(t_{1},f)e^{j2\pi ft}\,df{\text{ där }}tB<t_{1}<t+B$

Fast egendom

Rec-STFT har liknande egenskaper med Fourier-transform

• Integration

(a)

$\int _{-\infty }^{\infty }X(t,f)\,df=\int _{tB}^{t+B}x(\tau )\int _{-\ infty }^{\infty }e^{-j2\pi f\tau }\,df\,d\tau =\int _{tB}^{t+B}x(\tau )\delta (\tau) \,d\tau ={\begin{cases}\ x(0);&|t|<B\\\ 0;&{\text{annars}}\end{cases}}$

(b)

$\int _{-\infty }^{\infty }X(t,f)e^{-j2\pi fv}\,df={\begin{cases}\ x(v);&v- B<t<v+B\\\ 0;&{\text{annars}}\end{cases}}$

• Skiftande egenskap (skift längs x-axeln)

${\displaystyle \int _{tB}^{t+B}x(\tau +\tau _{0}) e^{-j2\pi f\tau }\,d\tau =X(t+\tau _{0},f)e^{j2\pi f\tau _{0}}} Moduleringsegenskap (skift$

• längs y -axel)

$\int _{tB}^{t+B}[x (\tau )e^{j2\pi f_{0}\tau }]d\tau =X(t,f-f_{0})$

• specialinmatning

1. När $x(t)=\delta (t),X(t,f)={\begin{cases}\ 1;&|t|<B\\\ 0;&{\text{annars}} \end{cases}}$
2. När $x(t)=1,X(t,f)=2B\operatörsnamn {sinc} (2Bf)e^{j2\pi ft}$

• Linjäritetsegenskap

Om $h(t)=\alpha x(t)+\beta y(t)\,$ , $H(t,f),X(t,f),$ och $Y(t,f)\,$ är deras rec-STFTs, då

$H(t,f)=\alpha X(t,f)+\beta Y(t,f).$

• Effektintegreringsegenskap

$\int _{-\infty }^{\infty }|X(t,f)|^{2}\,df=\int _{tB}^{t+B}|x( \tau )|^{2}\,d\tau$

${\displaystyle \int _{-\infty }^{\infty }\int _{-\infty }^{\infty }|X(t,f)|^{2}\,df\,dt =2B\int _{-\infty }^{\infty }|x(\tau )|^{2}\,d\tau } Energisummeegenskap ($

• Parsevals sats )

$\int _{-\infty }^{\infty }X(t,f)Y ^{*}(t,f)\,df=\int _{tB}^{t+B}x(\tau )y^{*}(\tau )\,d\tau$

$\int _{-\infty }^ {\infty }\int _{-\infty }^{\infty }X(t,f)Y^{*}(t,f)\,df\,dt=2B\int _{-\infty }^ {\infty }x(\tau )y^{*}(\tau )\,d\tau$

Exempel på avvägning med olika B

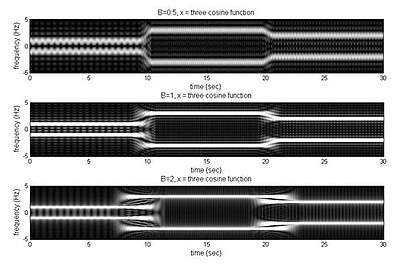
Spektrogram producerade från applicering av en rec-STFT på en funktion som består av 3 på varandra följande cosinusvågor. (det övre spektrogrammet använder mindre B på 0,5, mitten använder B av 1 och botten använder större B på 2.)

Från bilden, när B är mindre, är tidsupplösningen bättre. Annars, när B är större, är frekvensupplösningen bättre.

Fördelar och nackdelar

Jämfört med Fouriertransformen:

• Fördel: Den momentana frekvensen kan observeras.
• Nackdel: Högre komplexitet i beräkningen.

Jämfört med andra typer av tidsfrekvensanalys :

• Fördel: Minsta beräkningstid för digital implementering.
• Nackdel: Kvaliteten är sämre än andra typer av tids-frekvensanalys. Hoppdiskontinuiteten i kanterna på den rektangulära masken resulterar i Gibbs ringartefakter i frekvensdomänen, vilket kan lindras med mjukare fönster .

Se även

• Osäkerhetsprincip

1. Jian-Jiun Ding (2014) Tidsfrekvensanalys och wavelettransform