Regel 90
I den matematiska studien av cellulära automater är Regel 90 en elementär cellulär automat baserad på den exklusiva eller funktionen. Den består av en endimensionell array av celler, som var och en kan innehålla antingen ett 0- eller ett 1-värde. I varje tidssteg ersätts alla värden samtidigt av de exklusiva eller av deras två angränsande värden. Martin, Odlyzko & Wolfram (1984) kallar det "den enklaste icke-triviala cellulära automaten", och den beskrivs utförligt i Stephen Wolframs bok från 2002 A New Kind of Science .
När den startas från en enda levande cell har regel 90 ett tid-rymddiagram i form av en Sierpiński-triangel . Beteendet hos vilken annan konfiguration som helst kan förklaras som en överlagring av kopior av detta mönster, kombinerat med funktionen exklusiv eller . Varje konfiguration med endast ändligt många icke-nollceller blir en replikator som så småningom fyller arrayen med kopior av sig själv. När Regel 90 startas från en slumpmässig initial konfiguration, förblir dess konfiguration slumpmässig vid varje tidssteg. Dess tid-rymddiagram bildar många triangulära "fönster" av olika storlekar, mönster som bildas när en rad av celler i följd blir noll samtidigt och sedan flyttar celler med värde 1 gradvis in i denna rad från båda ändarna.
Några av de tidigaste studierna av regel 90 gjordes i samband med ett olöst problem i talteorin , Gilbreaths gissning , om skillnaderna mellan på varandra följande primtal . Denna regel är också kopplad till talteorin på ett annat sätt, via Goulds sekvens . Denna sekvens räknar antalet celler som inte är noll i varje tidssteg efter att regel 90 har börjat med en enda levande cell. Dess värden är potenser av två , med exponenter lika med antalet siffror som inte är noll i den binära representationen av stegnumret. Andra tillämpningar av regel 90 har inkluderat design av gobelänger .
Varje konfiguration av Regel 90 har exakt fyra föregångare, andra konfigurationer som bildar den givna konfigurationen efter ett enda steg. Därför, i motsats till många andra cellulära automater som Conways Game of Life , har Regel 90 ingen Edens trädgård , en konfiguration utan föregångare. Den ger ett exempel på en cellulär automat som är surjektiv (varje konfiguration har en föregångare) men inte injektiv (den har uppsättningar av mer än en konfiguration med samma efterföljare). Det följer av Edens trädgårdssats att Regel 90 är lokalt injektiv (alla konfigurationer med samma efterföljare varierar med ett oändligt antal celler).
Beskrivning
Regler
Regel 90 är en elementär cellulär automat . Det betyder att den består av en endimensionell array av celler, som var och en har ett enda binärt värde, antingen 0 eller 1. En tilldelning av värden till alla celler kallas en konfiguration . Automaten ges en initial konfiguration och fortsätter sedan genom andra konfigurationer i en sekvens av diskreta tidssteg. Vid varje steg uppdateras alla celler samtidigt. En fördefinierad regel bestämmer det nya värdet för varje cell som en funktion av dess tidigare värde och av värdena i dess två närliggande celler. Alla celler följer samma regel, som kan ges antingen som en formel eller som en regeltabell som anger det nya värdet för varje möjlig kombination av angränsande värden.
I fallet med regel 90 är varje cells nya värde det exklusiva eller av de två angränsande värdena. På motsvarande sätt styrs nästa tillstånd för denna speciella automat av följande regeltabell:
| nuvarande mönster | 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 |
|---|---|---|---|---|---|---|---|---|
| nytt tillstånd för mittcellen | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Namngivning
Namnet på regel 90 kommer från Stephen Wolframs binära decimalnotation för endimensionella cellulära automatregler. För att beräkna notationen för regeln, sammanfoga de nya tillstånden i regeltabellen till ett enda binärt tal och omvandla talet till decimal : 01011010 2 = 90 10 . Regel 90 har också kallats Sierpiński-automaten , på grund av den karakteristiska Sierpiński- triangelformen den genererar, och Martin–Odlyzko–Wolfram-cellautomaten efter Olivier Martins, Andrew M. Odlyzko och Stephen Wolframs ( 1984 ) tidiga forskning om detta. automat.
Egenskaper
Additivitet, superposition och nedbrytning
En konfiguration i regel 90 kan delas upp i två undergrupper av celler som inte interagerar med varandra. En av dessa två delmängder består av cellerna i jämna lägen vid jämna tidssteg och cellerna i udda lägen i udda tidssteg. Den andra delmängden består av cellerna i jämna positioner vid udda tidssteg och cellerna i udda positioner vid jämna tidssteg. Var och en av dessa två delmängder kan ses som en cellulär automat med endast hälften av cellerna. Regeln för automaten inom var och en av dessa delmängder är likvärdig (förutom en förskjutning med en halv cell per tidssteg) med en annan elementär cellulär automat, regel 102 , där det nya tillståndet för varje cell är exklusivt eller av dess gamla tillstånd och dess rätta granne. Det vill säga, beteendet för Regel 90 är i huvudsak detsamma som beteendet för två sammanflätade kopior av Regel 102.
Regel 90 och Regel 102 kallas för additiv cellulära automater . Detta betyder att om två initiala tillstånd kombineras genom att beräkna det exklusiva eller av vart och ett av deras tillstånd, så kommer deras efterföljande konfigurationer att kombineras på samma sätt. Mer generellt kan man dela upp vilken konfiguration som helst av regel 90 i två delmängder med osammanhängande celler som inte är noll, utveckla de två delmängderna separat och beräkna varje successiv konfiguration av den ursprungliga automaten som den exklusiva eller av konfigurationerna i samma tidssteg för de två delmängderna .
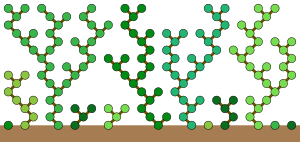
Stuntade träd och triangulära gläntor
Rule 90-automaten (i dess likvärdiga form på en av de två oberoende delmängderna av alternerande celler) undersöktes i början av 1970-talet, i ett försök att få ytterligare insikt i Gilbreaths gissningar om skillnaderna mellan på varandra följande primtal . I triangeln av tal som genereras från primtal genom att upprepade gånger använda framskillnadsoperatorn , verkar det som att de flesta värden är antingen 0 eller 2. I synnerhet hävdar Gilbreaths gissning att värdena längst till vänster i varje rad i denna triangel är alla 0 eller 2. När en sammanhängande undersekvens av värden i en rad i triangeln alla är 0 eller 2, kan Regel 90 användas för att bestämma motsvarande undersekvens i nästa rad. Miller (1970) förklarade regeln med en metafor om trädtillväxt i en skog, vilket gav titeln hans artikel om ämnet "Periodic forests of stunted trees". I denna metafor börjar ett träd växa vid varje position i den initiala konfigurationen vars värde är 1, och denna skog av träd växer sedan samtidigt, till en ny höjd över marken vid varje tidssteg. Varje cell som inte är noll vid varje tidssteg representerar en position som upptas av en växande trädgren. Vid varje på varandra följande tidssteg kan en gren växa till en av de två cellerna ovanför den till vänster och höger endast när det inte finns någon annan gren som konkurrerar om samma cell. En skog av träd som växer enligt dessa regler har exakt samma beteende som regel 90.
Från vilken initial konfiguration som helst av Regel 90 kan man bilda en matematisk skog , en riktad acyklisk graf där varje vertex har högst en utgående kant, vars träd är desamma som träden i Millers metafor. Skogen har en vertex för varje par ( x , i ) så att cell x inte är noll vid tidpunkten i . Topparna vid tidpunkten 0 har inga utgående kanter; var och en bildar roten till ett träd i skogen. För varje vertex ( x , i ) där i inte är noll går dess utgående kant till ( x ± 1, i − 1) , den unika granne som inte är noll i tidssteg i − 1 . Miller observerade att dessa skogar utvecklar triangulära "röjningar", regioner i tid-rymddiagrammet utan celler som inte är noll som begränsas av en platt bottenkant och diagonala sidor. En sådan röjning bildas när en på varandra följande sekvens av celler blir noll samtidigt i ett tidssteg, och sedan (i trädmetaforen) växer grenar inåt, och så småningom täcker sekvensens celler igen.
För slumpmässiga initiala förhållanden förskjuts själva gränserna mellan träden som bildas på detta sätt i ett till synes slumpmässigt mönster, och träd dör ofta ut helt och hållet. Men med hjälp av teorin om skiftregister kunde han och andra hitta initiala förhållanden där träden alla förblir vid liv för alltid, tillväxtmönstret upprepas med jämna mellanrum och alla röjningar kan garanteras förbli begränsade i storlek. Miller använde dessa upprepande mönster för att bilda gobelänger . Några av Millers gobelänger föreställer fysiska träd; andra visualiserar Rule 90-automaten med hjälp av abstrakta mönster av trianglar.
Sierpiński triangel

Tid-rymddiagrammet enligt regel 90 är ett diagram i vilket den i: te raden registrerar konfigurationen av automaten vid steg i . När det initiala tillståndet har en enda cell som inte är noll, ser detta diagram ut som Sierpiński-triangeln , en fraktal som bildas genom att kombinera trianglar till större trianglar. Reglerna 18, 22, 26, 82, 146, 154, 210 och 218 genererar också Sierpinski-trianglar från en enda cell, men alla dessa skapas inte helt identiskt. Ett sätt att förklara denna struktur använder sig av det faktum att, i regel 90, varje cell är den exklusiva eller av sina två grannar. Eftersom detta är ekvivalent med modulo -2-addition, genererar detta modulo-2-versionen av Pascals triangel . Diagrammet har en 1 där Pascals triangel har ett udda tal och en 0 där Pascals triangel har ett jämnt tal . Detta är en diskret version av Sierpiński-triangeln.
Antalet levande celler i varje rad i detta mönster är en potens av två . I den i: te raden är det lika med 2 k , där k är antalet siffror som inte är noll i den binära representationen av talet i . Sekvensen av dessa antal levande celler,
- 1, 2, 2, 4, 2, 4, 4, 8, 2, 4, 4, 8, 4, 8, 8, 16, 2, 4, 4, 8, 4, 8, 8, 16, 4, 8, 8, 16, 8, 16, 16, 32, ... (sekvens A001316 i OEIS )
är känd som Goulds sekvens . Den enda levande cellen i startkonfigurationen är ett sågtandsmönster . Detta innebär att antalet levande celler i vissa tidssteg växer godtyckligt stort medan de i andra återgår till endast två levande celler, oändligt ofta. Tillväxthastigheten för detta mönster har en karakteristisk växande sågtandsvågform som kan användas för att känna igen fysiska processer som beter sig på samma sätt som regel 90.
Sierpiński-triangeln förekommer också på ett mer subtilt sätt i utvecklingen av vilken konfiguration som helst i regel 90. När som helst i steg i i regelns utveckling kan tillståndet för vilken cell som helst beräknas som den exklusiva eller av en delmängd av cellerna i initial konfiguration. Den delmängden har samma form som den i: te raden i Sierpiński-triangeln.
Replikering
I Sierpiński-triangeln, för ett heltal i , har raderna numrerade med multiplar av 2 i celler som inte är noll åtskilda med minst 2 i -enheter från varandra. Därför, på grund av den additiva egenskapen i regel 90, om en initial konfiguration består av ett ändligt mönster P av celler som inte är noll med en bredd som är mindre än 2 i , då i steg som är multiplar av 2 i , kommer konfigurationen att bestå av kopior av P fördelade minst 2 i -enheter från start till start. Detta avstånd är tillräckligt stort för att förhindra att kopiorna stör varandra. Antalet kopior är detsamma som antalet celler som inte är noll i motsvarande rad i Sierpiński-triangeln. I den här regeln är alltså varje mönster en replikator : det genererar flera kopior av sig självt som sprids ut över konfigurationen och fyller så småningom hela arrayen. Andra regler inklusive Von Neumann universal constructor , Codds cellulära automat och Langtons loopar har också replikatorer som fungerar genom att bära och kopiera en sekvens av instruktioner för att bygga sig själva. Däremot är replikeringen i regel 90 trivial och automatisk.
Föregångare och Edens trädgårdar
I regel 90, på ett oändligt endimensionellt gitter, har varje konfiguration exakt fyra föregångare. Detta beror på att i en föregångare kan två på varandra följande celler ha vilken kombination av tillstånd som helst, men när de två cellernas tillstånd väl har valts finns det bara ett konsekvent val för tillstånden för de återstående cellerna. Därför finns det ingen Edens lustgård i regel 90, en konfiguration utan föregångare. Regel 90-konfigurationen som består av en enda icke-noll-cell (med alla andra celler noll) har inga föregångare som har ändligt många icke-noll. Den här konfigurationen är dock inte en Edens trädgård eftersom den har föregångare med oändligt många icke-nollor.
Det faktum att varje konfiguration har en föregångare kan sammanfattas genom att säga att regel 90 är surjektiv . Funktionen som mappar varje konfiguration till dess efterföljare är, matematiskt, en surjektiv funktion. Regel 90 är inte heller injektiv . I en injektiv regel har varannan konfiguration olika efterföljare, men regel 90 har par av konfigurationer med samma efterföljare. Regel 90 tillhandahåller ett exempel på en cellulär automat som är surjektiv men inte injektiv. The Garden of Eden-satsen av Moore och Myhill antyder att varje injektiv cellulär automat måste vara surjektiv, men detta exempel visar att det omvända inte är sant.
Eftersom varje konfiguration bara har ett begränsat antal föregångare, bevarar utvecklingen av regel 90 entropin för alla konfigurationer. I synnerhet, om en oändlig initial konfiguration väljs genom att välja tillståndet för varje cell oberoende slumpmässigt, där vart och ett av de två tillstånden är lika sannolikt att väljas, då kan varje efterföljande konfiguration beskrivas med exakt samma sannolikhetsfördelning.
Emulering av andra system
Många andra cellulära automater och andra beräkningssystem är kapabla att emulera beteendet hos regel 90. Till exempel kan en konfiguration i regel 90 översättas till en konfiguration till den olika elementära cellulära automaten regel 22. Översättningen ersätter varje regel 90-cell med tre på varandra följande regel 22-celler. Dessa celler är alla noll om regel 90-cellen själv är noll. En cell som inte är noll regel 90 översätts till en etta följt av två nollor. Med denna transformation simulerar vart sjätte steg i Rule 22-automaten ett enda steg av Rule 90-automaten. Liknande direkta simuleringar av Regel 90 är också möjliga för de elementära cellulära automaterna Regel 45 och Regel 126, för vissa strängomskrivningssystem och taggsystem , och i vissa tvådimensionella cellulära automater inklusive Wireworld . Regel 90 kan också simulera sig själv på samma sätt. Om varje cell i en Regel 90-konfiguration ersätts av ett par på varandra följande celler, den första innehåller den ursprungliga cellens värde och den andra innehåller noll, så har denna dubblerade konfiguration samma beteende som den ursprungliga konfigurationen vid halva hastigheten.
Olika andra cellulära automater är kända för att stödja replikatorer, mönster som gör kopior av sig själva, och de flesta delar samma beteende som i trädtillväxtmodellen för regel 90. En ny kopia placeras på vardera sidan av replikatormönstret, så länge som utrymme där är tomt. Men om två replikatorer båda försöker kopiera sig själva till samma position förblir utrymmet tomt. I båda fallen försvinner replikatorerna själva och lämnar sina kopior för att fortsätta replikeringen. Ett standardexempel på detta beteende är "bowtie pasta"-mönstret i den tvådimensionella HighLife- regeln. Den här regeln beter sig på många sätt som Conways Game of Life, men en så liten replikator finns inte i Life. Närhelst en automat stöder replikatorer med samma tillväxtmönster, kan endimensionella arrayer av replikatorer användas för att simulera regel 90. Regel 90 (på ändliga rader av celler) kan också simuleras av blockoscillatorerna i de tvådimensionella Life - like cellulär automat B36/S125, även kallad "2x2", och beteendet enligt regel 90 kan användas för att karakterisera de möjliga perioderna för dessa oscillatorer.