Problem med minsta cirkel

Några instanser av den minsta avgränsande cirkeln.

den minsta cirkeln (även känt som problem med minsta täckande cirkel , problem med begränsande cirkel , problem med minsta cirkel , problem med minsta omslutande cirkel) är ett matematiskt problem för att beräkna den minsta cirkeln som innehåller alla en given uppsättning punkter i det euklidiska planet . Motsvarande problem i n -dimensionell rymd , det minsta gränssfärproblemet, är att beräkna den minsta n -sfären som innehåller alla en given uppsättning punkter. Problemet med den minsta cirkeln föreslogs ursprungligen av den engelske matematikern James Joseph Sylvester 1857.

Det minsta cirkelproblemet i planet är ett exempel på ett lokaliseringsproblem ( 1-centerproblemet ) där platsen för en ny anläggning måste väljas för att ge service till ett antal kunder, vilket minimerar det längsta avståndet som en kund måste resa för att nå den nya anläggningen. Både det minsta cirkelproblemet i planet och det minsta gränssfärproblemet i något högredimensionellt utrymme med begränsad dimension är lösbara i linjär tid i värsta fall .

Karakterisering

De flesta av de geometriska tillvägagångssätten för problemet letar efter punkter som ligger på gränsen för minimicirkeln och är baserade på följande enkla fakta:

Den minsta täckande cirkeln är unik.
Den minsta täckande cirkeln för en mängd S kan bestämmas av högst tre punkter i S som ligger på cirkelns gräns. Om det bara bestäms av två punkter, linjesegmentet som förenar dessa två punkter vara en diameter av den minsta cirkeln. Om det bestäms av tre punkter, triangeln som består av dessa tre punkter inte trubbig .

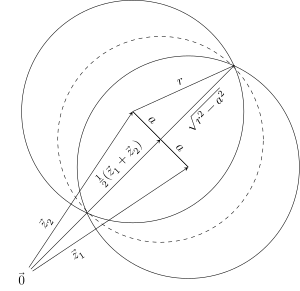
Bevis på att den minsta täckskivan är unik

Låt P vara vilken som helst uppsättning punkter i planet, och anta att det finns två minsta omslutande skivor av P , med centrum vid ${\vec {z}}_{1}$ och ${\ displaystyle {\vec {z}}_{2}}$ . Låt $r$ vara deras delade radie och låt $2a$ vara avståndet mellan deras mittpunkter. Eftersom P är en delmängd av båda diskarna är det en delmängd av deras skärningspunkt . Deras skärningspunkt finns dock inom skivan med mitten ${\frac {1}{2}}({\vec {z}}_{1}+{\ vec {z}}_{2})$ och radie ${\displaystyle {\sqrt {r^{2}-a^{2}}}} ,$ som visas i följande bild:

Eftersom r är minimal måste vi ha ${\displaystyle {\sqrt {r^{2}-a^{2}}}=r} ,$ vilket betyder $a=0$ , så diskarna är identiska.

Linjära tidslösningar

Som Nimrod Megiddo visade, kan den minsta omslutande cirkeln hittas i linjär tid, och samma linjära tidsgräns gäller även för den minsta omslutande sfären i euklidiska rum av någon konstant dimension. Hans artikel ger också en kort översikt över tidigare $O(n^{3})$ och $O(n\log n)$ algoritmer; genom att göra det visade Megiddo att Shamos och Hoeys gissningar – att en lösning på problemet med den minsta cirkeln var beräkningsbar i $\Omega (n\log n)$ i bästa fall var falsk.

Emo Welzl föreslog en enkel randomiserad algoritm för det minsta täckande cirkelproblemet som körs i förväntad tid ${\displaystyle O(n)} ,$ baserad på en linjär programmeringsalgoritm av Raimund Seidel .

Därefter inkluderades det minsta cirkelproblemet i en allmän klass av LP-typproblem som kan lösas med algoritmer som Welzls baserade på linjär programmering. Som en konsekvens av medlemskapet i denna klass visades det att beroendet av dimensionen av den konstanta faktorn i $O(n)$ tidsgräns, som var faktoriell för Seidels metod, kunde reduceras till subexponentiell .

Megiddos algoritm

Körning av Megiddos algoritmfas, kassering från punktuppsättning A, B, ..., U onödiga punkter E, T.

Megiddos algoritm är baserad på tekniken som kallas prune and search, vilket minskar storleken på problemet genom att ta bort ${\textstyle {\frac {n}{16}}}$ onödiga punkter. Det leder till att $t(n)\leq t\left({\frac {15n}{16}}\right)+cn$ ger $t(n)=16cn$ .

Algoritmen är ganska komplicerad och den återspeglas av dess stora multiplikationskonstant. Reduktionen måste lösa dubbelt så mycket liknande problem där mitten av den eftersökta omslutande cirkeln är begränsad till att ligga på en given linje . Lösningen av delproblemet är antingen lösningen av det obegränsade problemet eller så används det för att bestämma halvplanet där det obegränsade lösningscentrumet är beläget.

De ${\textstyle {\frac {n}{16}}}$ punkterna som ska kasseras hittas enligt följande: Punkterna Pi _{ är ordnade i par som definierar $\textstyle {\frac {n}{2} }}$ linjer p _j som deras bisektorer . Medianmedelvärdet p _m av bisektrar i ordning efter deras riktningar (orienterat till samma halvplan som bestäms av bisektris $p 1$ ) hittas och halvledspar görs, så att i varje par en bisektur har högst riktning p _m och annat åtminstone p _m (riktning $p 1$ skulle kunna betraktas som − $\infty$ eller + $\infty$ enligt våra behov.) Låt Q _k vara skärningspunkten för bisektrarna i det k -:te paret .

Linjen q i $p 1$ -riktningen placeras så att den går genom en skärningspunkt Q _x så att det finns ${\textstyle {\frac {n}{8}}}$ skärningar i varje halvplan som definieras av linjen (medianposition ). Den begränsade versionen av det inneslutande problemet körs på linjen q' som bestämmer halvplanet där centrum är beläget. Linjen q ′ i riktningen p _m är placerad för att gå genom en skärningspunkt Q _x' så att det finns ${\textstyle {\frac {n}{16}}}$ skärningar i varje halva av halvplanet som inte innehåller lösningen. Den begränsade versionen av det omslutande problemet körs på linjen q ′ som tillsammans med q bestämmer kvadranten där centrum är beläget. Vi betraktar punkterna Qk i kvadranten som inte finns _i ett halvplan som innehåller lösningen. En av halvledarna i paret som definierar Qk _. har riktningen som säkerställer vilken av punkterna Pi _som definierar bisektrisen som är närmast varje punkt i kvadranten som innehåller centrum av den omslutande cirkeln Denna punkt kan förkastas.

Den begränsade versionen av algoritmen löses också med beskärnings- och söktekniken, men genom att minska problemets storlek genom att ta bort ${\textstyle {\frac {n}{4}}}$ punkter som leder till upprepning

t(n)\leq t\left({\frac {3n}{4}}\right)+cn

ger $t(n)=4cn$ .

De ${\textstyle {\frac {n}{4}}}$ punkterna som ska kasseras hittas enligt följande: Punkterna P _i är ordnade i par. För varje par hittas skärningspunkten Q _j för dess halveringslinje med den begränsande linjen q (Om denna skärningspunkt inte finns kan vi ta bort en punkt från paret omedelbart). Medianen M för punkterna Q _j på linjen q hittas och i O ( n ) bestäms tiden vilken halvlinje av q som börjar i M som innehåller lösningen av det begränsade problemet. Vi betraktar punkterna Q _j från den andra halvan. Vi vet vilken av punkterna Pi _som definierar Q _j som är närmare varje punkt på halvlinjen som innehåller centrum för den omslutande cirkeln för den begränsade problemlösningen. Denna punkt kan förkastas.

Halvplanet där den obegränsade lösningen ligger skulle kunna bestämmas av punkterna Pi på _gränsen för lösningen med begränsad cirkel. (Den första och sista punkten på cirkeln i varje halvplan räcker. Om mitten hör till deras konvexa skrov är det en obunden lösning, annars bestämmer riktningen till närmaste kant halvplanet för den obegränsade lösningen.)

Welzls algoritm

Algoritmen är rekursiv .

Den initiala inmatningen är en uppsättning P av punkter. Algoritmen väljer en punkt p slumpmässigt och enhetligt från P , och hittar rekursivt den minimala cirkeln som innehåller P – { p }, dvs alla andra punkter i P utom p . Om den returnerade cirkeln också omsluter p , är det den minimala cirkeln för hela P och returneras.

Annars måste punkt p ligga på gränsen för resultatcirkeln. Det återkommer, men med uppsättningen R av punkter som är kända för att vara på gränsen som en extra parameter.

Rekursionen slutar när P är tomt , och en lösning kan hittas från punkterna i R : för 0 eller 1 punkter är lösningen trivial, för 2 punkter har den minimala cirkeln sitt centrum i mitten mellan de två punkterna, och för 3 punkter cirkeln är den omslutna cirkeln av triangeln som beskrivs av punkterna. (I tre dimensioner kräver 4 punkter beräkningen av en tetraeders omkrets .)

Rekursionen kan också avslutas när R har storlek 3 (i 2D, eller 4 i 3D) eftersom de återstående punkterna i P måste ligga inom cirkeln som beskrivs av R .

     
           
         

     algoritm  welzl  matas  in:  Finita sätter  P  och  R  av punkter i planet |  R  | ≤ 3.   utgång:  Minimal skiva som omsluter  P  med  R  på gränsen.  om  P  är tomt  eller  |  R  | = 3   returnera  sedan  trivial(  R  )  välj  p  i  P  (  slumpmässigt  och  likformigt  ) D := welzl(  P  − {  p  },  R  )  om  p  är i  D  returnera  D  returnera  welzl  (  P  − {  p  },  R  ∪ {  p  })

Welzls papper säger att det är tillräckligt att slumpmässigt permutera inmatningen i början, snarare än att utföra oberoende slumpmässiga val av p på varje rekursion.

Det sägs också att prestandan förbättras genom att dynamiskt omordna punkterna så att de som befinns vara utanför en cirkel därefter betraktas tidigare, men detta kräver en förändring i strukturen av algoritmen för att lagra P som en "global " .

Andra algoritmer

Innan Megiddos resultat visade att problemet med den minsta cirkeln kan lösas i linjär tid, förekom flera algoritmer med högre komplexitet i litteraturen. En naiv algoritm löser problemet i tid O( n ⁴ ) genom att testa cirklarna som bestäms av alla par och trippel av punkter.

En algoritm av Chrystal och Peirce tillämpar en lokal optimeringsstrategi som upprätthåller två punkter på gränsen till en omslutande cirkel och upprepade gånger krymper cirkeln, och ersätter paret av gränspunkter, tills en optimal cirkel hittas. Chakraborty och Chaudhuri föreslår en linjär-tidsmetod för att välja en lämplig initial cirkel och ett par gränspunkter på den cirkeln. Varje steg i algoritmen inkluderar som en av de två gränspunkterna en ny vertex av det konvexa skrovet , så om skrovet har h hörn kan denna metod implementeras för att köras i tiden O( nh ).
Elzinga och Hearn beskrev en algoritm som upprätthåller en täckande cirkel för en delmängd av punkterna. Vid varje steg används en punkt som inte täcks av den aktuella sfären för att hitta en större sfär som täcker en ny delmängd av punkter, inklusive den hittade punkten. Även om dess värsta gångtid är O( h ³ n ), rapporterar författarna att den kördes i linjär tid i sina experiment. Metodens komplexitet har analyserats av Drezner och Shelah. Både Fortran- och C -koder är tillgängliga från Hearn, Vijay & Nickel (1995) .
Det minsta sfärproblemet kan formuleras som ett kvadratiskt program definierat av ett system av linjära begränsningar med en konvex kvadratisk objektivfunktion. Därför kan vilken som helst genomförbar riktningsalgoritm ge lösningen på problemet. Hearn och Vijay bevisade att den genomförbara riktningsstrategin som valts av Jacobsen är likvärdig med Chrystal-Peirce-algoritmen.
Dualen till detta kvadratiska program kan också formuleras explicit; en algoritm av Lawson kan beskrivas på detta sätt som en primär dubbelalgoritm.
Shamos och Hoey föreslog en O( n log n ) tidsalgoritm för problemet baserat på observationen att centrum för den minsta omslutande cirkeln måste vara en vertex av Voronoi-diagrammet längst bort i ingångspunktsmängden.

Viktade varianter av problemet

Den viktade versionen av problemet med minsta täckande cirkel tar som indata en uppsättning punkter i ett euklidiskt utrymme, var och en med vikter; Målet är att hitta en enda punkt som minimerar det maximala viktade avståndet till någon punkt. Det ursprungliga problemet med minsta täckande cirkel kan återställas genom att sätta alla vikter till samma nummer. Liksom med det oviktade problemet kan det viktade problemet lösas i linjär tid i vilket utrymme som helst med begränsad dimension, genom att använda tillvägagångssätt som är nära besläktade med linjära programmeringsalgoritmer för begränsad dimension, även om långsammare algoritmer återigen är vanliga i litteraturen.

Se även

externa länkar

Bernd Gärtners minsta bifogade bollkod
CGAL paketet Min_sphere_of_spheres i Computational Geometry Algorithms Library (CGAL)
Miniball en öppen källkodsimplementering av en algoritm för det minsta problemet med omslutande boll för låga och måttligt höga dimensioner