Potentiellt flöde runt en cirkulär cylinder

I matematik är potentiellt flöde runt en cirkulär cylinder en klassisk lösning för flödet av en inviscid , inkompressibel vätska runt en cylinder som är tvärgående mot flödet. Långt från cylindern är flödet enkelriktat och enhetligt. Flödet har ingen vorticitet och därmed är hastighetsfältet irroterande och kan modelleras som ett potentiellt flöde . Till skillnad från en riktig vätska, indikerar denna lösning ett netto nolldrag på kroppen, ett resultat som kallas d'Alemberts paradox .

Matematisk lösning

Färger: tryckfält. Rött är högt och blått är lågt. Hastighetsvektorer.

Närbild av en kvadrant av flödet. Färger: tryckfält. Rött är högt och blått är lågt. Hastighetsvektorer.

Tryckfält (färger), strömfunktion ( svart ) med konturintervall på 0,2 Ur från botten till topp, hastighetspotential ( vit ) med konturintervall 0,2 Ur från vänster till höger.

En cylinder (eller skiva) med radien R placeras i ett tvådimensionellt, inkompressibelt, inviscid flöde. Målet är att hitta den konstanta hastighetsvektorn V och trycket p i ett plan, under förutsättning att långt från cylindern är hastighetsvektorn (i förhållande till enhetsvektorerna i och j ):

$\mathbf {V} =U\mathbf {i} +0\mathbf {j} \,,$

där U är en konstant, och vid cylinderns gräns

$\mathbf {V} \cdot \mathbf {\hat {n}} =0\,,$

där n̂ är vektorn normal till cylinderytan. Uppströmsflödet är enhetligt och har ingen virvel. Flödet är inviscid, inkompressibelt och har konstant massdensitet ρ . Flödet förblir därför utan virvel, eller sägs vara irroterande , med ∇ × V = 0 överallt. Eftersom det är irroterande måste det finnas en hastighetspotential φ :

$\mathbf {V} =\nabla \phi \,.$

∇ · V = 0 är inkompressibel , måste φ uppfylla Laplaces ekvation :

$\nabla ^{2}\phi =0\,.$

Lösningen för φ erhålls enklast i polära koordinater r och θ , relaterade till konventionella kartesiska koordinater med x = r cos θ och y = r sin θ . I polära koordinater är Laplaces ekvation (se Del i cylindriska och sfäriska koordinater ):

${\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial \phi }{\partial r}}\right)+{ \frac {1}{r^{2}}}{\frac {\partial ^{2}\phi }{\partial \theta ^{2}}}=0\,.$

Lösningen som uppfyller randvillkoren är

$\phi (r,\theta )=Ur\left(1+{\frac {R^{2}}{r^{2}}}\right)\cos \theta \,.$

Hastighetskomponenterna i polära koordinater erhålls från komponenterna av ∇ φ i polära koordinater:

$V_{r}={\frac {\partial \phi }{\partial r}}=U\left(1- {\frac {R^{2}}{r^{2}}}\right)\cos \theta$

och

$V_{\theta }={\frac {1}{r}}{\frac {\partial \phi }{\partial \theta }}=-U\left(1+{\frac {R^{ 2}}{r^{2}}}\right)\sin \theta \,.$

Eftersom Bernoullis ekvation är inviscid och irroterande tillåter lösningen för tryckfältet att erhållas direkt från hastighetsfältet:

$p={\tfrac {1}{2}}\rho \left(U^{2}-V^{2}\right) +p_{\infty },$

där konstanterna U och p _∞ visas så att p → p _∞ långt från cylindern, där V = U . Genom att använda V ² = V
² _r + V
² _θ ,

$p={\tfrac {1}{2}}\rho U^{2}\left(2{\frac {R^{2}}{r^{2}}}\cos(2\theta )-{\frac {R^{4}}{r^{4}}}\right)+p_{\infty }\,.$

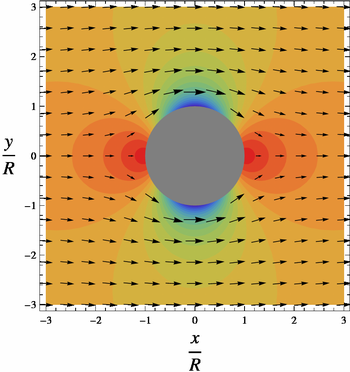
I figurerna är det färgade fältet som kallas "tryck" en plot av

$2{\frac {p-p_{\infty }}{\rho U^{2}}}=2{\frac {R^{2}}{r^{2}}}\cos(2 \theta )-{\frac {R^{4}}{r^{4}\,}}.$

På cylinderns yta, eller r = R , varierar trycket från maximalt 1 (visas i diagrammet i rött ) vid stagnationspunkterna vid θ = 0 och θ = π till ett minimum av −3 (visas i blått ) på cylinderns sidor, vid θ = π / 2 och θ = 3π / 2 . Likaså V från V = 0 vid stagnationspunkterna till V = 2 U på sidorna, i lågtrycket.

Stream funktion

Eftersom flödet är inkompressibelt kan en strömningsfunktion hittas sådan att

$\mathbf {V} =\nabla \psi \times \mathbf {k} \,.$

Det följer av denna definition, med hjälp av vektoridentiteter ,

$\mathbf {V} \cdot \nabla {\psi }=0\,.$

Därför kommer en kontur med ett konstant värde på ψ också att vara en strömlinje, en linje som tangerar V . För flödet förbi en cylinder finner vi:

$\psi =U\left(r-{\frac {R^{2}}{r}}\right)\sin \theta \,.$

Fysisk tolkning

Laplaces ekvation är linjär och är en av de mest elementära partiella differentialekvationerna . Denna enkla ekvation ger hela lösningen för både V och p på grund av begränsningen av irrotationalitet och inkompressibilitet. Efter att ha erhållit lösningen för V och p kan tryckgradientens överensstämmelse med accelerationerna noteras.

Det dynamiska trycket 1/2 . vid ρU ² stagnationspunkten uppströms har ett värde av ett värde som behövs för att bromsa det fria flödet av hastighet U . Samma värde visas vid stagnationspunkten nedströms, detta höga tryck behövs återigen för att bromsa flödet till nollhastighet. Denna symmetri uppstår endast för att flödet är helt friktionsfritt.

Det låga trycket på sidorna på cylindern behövs för att ge flödets centripetalacceleration :

${\frac {\partial p}{\partial r}}={\frac {\rho V^{2}}{L}}\,,$

där L är krökningsradien för flödet. Men L ≈ R , och V ≈ U . Integralen av ekvationen för centripetalacceleration över en sträcka Δ r ≈ R kommer alltså att ge

$p-p_{\infty }\approx -\rho U^{2}\,.$

Den exakta lösningen har, för det lägsta trycket,

$p-p_{\infty }=-{\tfrac {3}{2}}\rho U^{2}\,.$

Det låga trycket, som måste vara närvarande för att ge centripetalaccelerationen, kommer också att öka flödeshastigheten när vätskan färdas från högre till lägre tryckvärden. Således finner vi maxhastigheten i flödet, V = 2 U , i lågtrycket på cylinderns sidor.

Ett värde på V > U överensstämmer med bevarandet av vätskevolymen. När cylindern blockerar en del av flödet V vara större än U någonstans i planet genom cylinderns mitt och tvärs flödet.

Jämförelse med flödet av en riktig vätska förbi en cylinder

Symmetrin i denna idealiska lösning har en stagnationspunkt på baksidan av cylindern, såväl som på framsidan. Tryckfördelningen över fram- och baksidan är identisk, vilket leder till den speciella egenskapen att ha noll drag på cylindern, en egenskap som kallas d'Alemberts paradox . Till skillnad från en idealisk inviscid vätska kommer ett viskös flöde förbi en cylinder, oavsett hur liten viskositeten är, att få ett tunt gränsskikt intill cylinderns yta. Gränsskiktseparation kommer att inträffa och ett efterföljande kölvatten kommer att finnas i flödet bakom cylindern. Trycket vid varje punkt på cylinderns vaksida kommer att vara lägre än på uppströmssidan, vilket resulterar i en dragkraft i nedströmsriktningen.

Janzen–Rayleigh expansion

Problemet med potentiellt komprimerbart flöde över cirkulär cylinder studerades först av O. Janzen 1913 och av Lord Rayleigh 1916 med små komprimerbara effekter. Här är den lilla parametern kvadraten på Mach-talet $\mathrm {M} ^{2}=U^{2}/c^{2}\ll 1$ , där c är ljudets hastighet . Då är lösningen på första ordningens approximation vad gäller hastighetspotentialen

$\phi (r,\theta )=Ur\left(1+{\frac {a^{2}} {r^{2}}}\right)\cos \theta -\mathrm {M} ^{2}{\frac {Ur}{12}}\left[\left({\frac {13a^{2} }{r^{2}}}-{\frac {6a^{4}}{r^{4}}}+{\frac {a^{6}}{r^{6}}}\right) \cos \theta +\left({\frac {a^{4}}{r^{4}}}-{\frac {3a^{2}}{r^{2}}}\right)\cos 3\theta \right]+\mathrm {O} \left(\mathrm {M} ^{4}\right)\,$

där $a$ är cylinderns radie.

Potentiellt flöde över en cirkulär cylinder med små variationer

Regelbunden störningsanalys för ett flöde runt en cylinder med lätt störning i konfigurationerna finns i Milton Van Dyke (1975). I det följande ε att representera en liten positiv parameter och a är cylinderns radie. För mer detaljerade analyser och diskussioner hänvisas läsarna till Milton Van Dykes bok 1975 Perturbation Methods in Fluid Mechanics .

Något förvriden cylinder

Här är cylinderns radie inte r = a , utan en något förvrängd form r = a (1 − ε sin ² θ ) . Då är lösningen på första ordningens approximation

$\psi (r,\theta )=Ur\left(1-{\frac {a^{2}}{r^{2}}}\right)\sin \theta +\varepsilon {\frac { Ur}{2}}\left({\frac {3a^{2}}{r^{2}}}\sin \theta -{\frac {a^{4}}{r^{4}}} \sin 3\theta \right)+\mathrm {O} \left(\varepsilon ^{2}\right)$

Något pulserande cirkel

Här varierar cylinderns radie något med tiden så   r = a (1 + ε f ( t )) . Då är lösningen på första ordningens approximation

$\psi (r,\theta ,t)=Ur\left(1-{\frac {a^{2}}{r^{2}}}\right)\sin \theta +\varepsilon Ur\left({\frac {a^{2}}{Ur}}\theta f'(t)-{\frac {2a^{2}}{r^{2}}}f (t)\sin \theta \right)+\mathrm {O} \left(\varepsilon ^{2}\right)$

Flöda med lätt virvel

I allmänhet är friströmshastigheten U likformig, med andra ord ψ = Uy , men här påläggs en liten virvel i det yttre flödet.

Linjär skjuvning

Här införs en linjär skjuvning i hastigheten.

${\begin{aligned}\psi &=U\left(y+{ \frac {1}{2}}\varepsilon {\frac {y^{2}}{a}}\right)\,,\\[3pt]\omega &=-\nabla ^{2}\psi = -\varepsilon {\frac {U}{a}}\quad {\text{som }}x\högerpil -\infty \,,\end{aligned}}$

där ε är den lilla parametern. Den styrande ekvationen är

$\nabla ^{2}\psi =-\omega (\psi )\,.$

Då är lösningen på första ordningens approximation

$\psi (r,\theta )=Ur\left(1-{\frac {a^{2}}{r^{2}}}\right)\sin \theta +\varepsilon {\frac { Ur}{4}}\left({\frac {r}{a}}(1-\cos 2\theta )+{\frac {a^{3}}{r^{3}}}\cos 2 \theta -{\frac {a}{r}}\right)+\mathrm {O} \left(\varepsilon ^{2}\right)\,.$

Parabolskjuvning

Här införs en parabolisk skjuvning i den yttre hastigheten.

${\begin{aligned}\psi &=U\left(y+{\tfrac {1}{6}}\varepsilon {\frac {y^{3}}{a^{2}}}\right )\,,\\\omega &=-\nabla ^{2}\psi =-\varepsilon U{\frac {y}{a^{2}}}\quad {\text{as }}x\rightarrow -\infty \,.\end{aligned}}$

Då är lösningen på första ordningens approximation

$\psi (r,\theta )=Ur\left(1-{\frac {a^{2}}{r^{2}}}\right)\sin \theta +\varepsilon { \frac {Ur}{6}}\left({\frac {r^{2}}{a^{2}}}\sin ^{2}\theta -3r\ln r\sin \theta +\chi \right)+\mathrm {O} \left(\varepsilon ^{2}\right)\,,$

där χ är den homogena lösningen till Laplace-ekvationen som återställer randvillkoren.

Något porös cylinder

Låt C _ps representera yttryckskoefficienten för en ogenomtränglig cylinder:

$C_{\mathrm {ps} }={\frac {p_{s }-p_{\infty }}{{\tfrac {1}{2}}\rho U^{2}}}=1-4\sin ^{2}\theta =2\cos 2\theta -1\ ,,$

där p _s är yttrycket för den ogenomträngliga cylindern. Låt nu Cpi _av vara den inre tryckkoefficienten inuti cylindern, då ges en lätt normal hastighet på grund av den lätta porösheten

${\frac {1}{r }}{\frac {\partial \psi }{\partial \theta }}=\varepsilon U\left(C_{\mathrm {pi} }-C_{\mathrm {ps} }\right)=\varepsilon U\ vänster(C_{\mathrm {pi} }+1-2\cos 2\theta \right)\quad {\text{at }}r=a\,,$

men villkoret noll nettoflöde

$\int _{0}^{2\pi }{\frac {1}{r}}{\frac {\partial \psi }{\partial \ theta }}\,\mathrm {d} \theta =0$

kräver att C _pi = −1 . Därför,

${\frac {\partial \psi }{\partial \theta }}=-2\varepsilon rU\cos 2\theta \quad {\text{at }}r=a\,.$

Då är lösningen på första ordningens approximation

$\psi (r,\theta )=Ur\left(1-{\frac {a^{2}}{r^{2}}}\right)\sin \theta -\varepsilon U{\frac {a^{3}}{r^{2}}}\sin 2\theta +\mathrm {O} \left(\varepsilon ^{2}\right)\,.$

Korrugerad kvasi-cylinder

Om cylindern har variabel radie i axiell riktning, z -axeln, r = a ( 1 + ε sin z / b ) , så är lösningen till första ordningens approximation i termer av den tredimensionella hastighetspotentialen

$\phi (r,\theta ,z)=Ur\left(1+{\frac {a^{2}}{r^{2}}}\right)\cos \theta - 2\varepsilon Ub{\frac {K_{1}\left({\frac {r}{b}}\right)}{K_{1}'\left({\frac {r}{b}}\right )}}\cos \theta \sin {\frac {z}{b}}+\mathrm {O} \left(\varepsilon ^{2}\right)\,,$

där K ₁ ( r / b ) är den modifierade Bessel-funktionen av första ordningens etta.

Se även

• Joukowsky förvandling
• Kutta skick
• Magnus effekt