Oktaedrisk pyramid

Octaedral pyramid
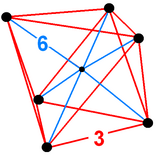
Schlegel diagram
Typ	Polyedrisk pyramid
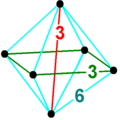
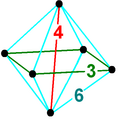
Schläfli symbol	( ) ∨ {3,4} ( ) ∨ r{3,3} ( ) ∨ s{2,6} ( ) ∨ [{4} + { }] ( ) ∨ [{ } + { } + { }]
Celler	9	1 {3,4} 8 ( ) ∨ {3}
Ansikten	20 {3}
Kanter	18
Vertices	7
Dubbel	Kubisk pyramid
Symmetrigrupp	B ₃ , [4,3,1], order 48 [3,3,1], order 24 [2 ⁺ ,6,1], order 12 [4,2,1], order 16 [2,2,1 ], order 8
Egenskaper	konvexa , regelbundna celler, Blind polytop

I 4-dimensionell geometri begränsas den oktaedriska pyramiden av en oktaeder på basen och 8 triangulära pyramidceller som möts i spetsen. Eftersom en oktaeder har en cirkumradius dividerad med kantlängd mindre än en, kan de triangulära pyramiderna göras med regelbundna ytor (som vanliga tetraeder ) genom att beräkna lämplig höjd.

Med alla vanliga celler är det en blind polytop . Två kopior kan utökas för att göra en oktaedrisk bipyramid som också är en blind polytop.

Förekomster av den oktaedriska pyramiden

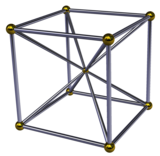
Den vanliga 16-cellen har oktaedriska pyramider runt varje vertex, med oktaedern som passerar genom mitten av 16-cellen. Att placera två regelbundna oktaedriska pyramider bas mot bas konstruerar därför en 16-cell. Den 16-celliga tesslar ett 4-dimensionellt utrymme som en 16-cells honungskaka .

Exakt 24 vanliga oktaedriska pyramider kommer att passa ihop runt en vertex i ett fyrdimensionellt utrymme (toppen av varje pyramid). Denna konstruktion ger en 24-cell med oktaedriska begränsningsceller, som omger en central vertex med 24 långa radier av kantlängd. Det 4-dimensionella innehållet i en 24-cells enhetskantlängd är 2, så innehållet i den vanliga oktaedriska pyramiden är 1/12. Den 24-celliga tesslar ett 4-dimensionellt utrymme som en 24-cells honungskaka .

Den oktaedriska pyramiden är vertexfiguren för en trunkerad 5-ortoplex , .

Grafen för den oktaedriska pyramiden är det enda möjliga minimala motexemplet till Negamis gissning , att de sammankopplade graferna med plana höljen i sig själva är projektiva-plana.

Exempel 4-dimensionella koordinater, 6 punkter i de första 3 koordinaterna för kub och 4:e dimensionen för spetsen.

(±1, 0, 0; 0)

( 0,±1, 0; 0)

( 0, 0,±1; 0)

( 0, 0, 0; 1)

Andra polytoper

Kubisk pyramid

Dualen till den oktaedriska pyramiden är en kubisk pyramid , sedd som en kubisk bas och 6 kvadratiska pyramider som möts i en spets .

Exempel 4-dimensionella koordinater, 8 punkter i de första 3 koordinaterna för kub och 4:e dimensionen för spetsen.

(±1,±1,±1; 0)

( 0, 0, 0; 1)

Fyrkantig pyramidformad pyramid

Fyrkantig pyramidformad pyramid

Typ	Polyedrisk pyramid
Schläfli symbol	( ) ∨ [( ) ∨ {4}] [( )∨( )] ∨ {4} = { } ∨ {4} { } ∨ [{ } × { }] { } ∨ [{ } + { }]
Celler	6	2 { } ∨ {4} 4 { } ∨ {3}
Ansikten	12 {3} 1 {4}
Kanter	13
Vertices	6
Dubbel	Självdubbel
Symmetrigrupp	[4,1,1], order 8 [4,2,1], order 16 [2,2,1], order 8
Egenskaper	konvex , regelbunden ansikte

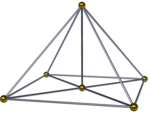
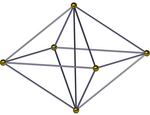
Den fyrkantiga pyramidpyramiden , ( ) ∨ [( ) ∨ {4}], är en tvådelad oktaedrisk pyramid. Den har en fyrkantig pyramidbas och 4 tetraedrar tillsammans med ytterligare en fyrkantig pyramid som möts i spetsen. Den kan också ses i en kantcentrerad projektion som en fyrkantig bipyramid med fyra tetraedrar lindade runt den gemensamma kanten. Om höjden på de två spetsarna är densamma kan den ges ett högre symmetrinamn [( ) ∨ ( )] ∨ {4} = { } ∨ {4}, vilket förenar en kant till en vinkelrät kvadrat.

Den fyrkantiga pyramidalpyramiden kan förvrängas till en rektangulär-pyramidal pyramid , { } ∨ [{ } × { }] eller en rombisk-pyramidal pyramid , { } ∨ [{ } + { }], eller andra lägre symmetriformer.

Den fyrkantiga-pyramidal pyramiden existerar som en vertex figur i enhetliga polytopes av formen, inklusive bitruncated 5-orthoplex och bitruncated tesseractic honeycomb .