Kubisk pyramid
| Kubisk pyramid | ||
|---|---|---|
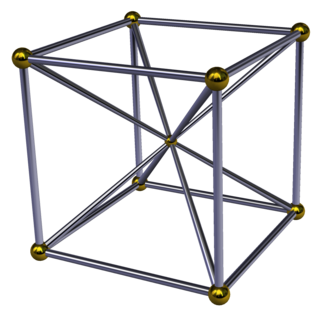 Schlegel diagram |
||
| Typ | Polyedrisk pyramid | |
| Schläfli symboler |
( ) ∨ {4,3} ( ) ∨ [{4} × { }] ( ) ∨ [{ } × { } × { }] |
|
| Celler | 7 | 1 {4,3} 6 ( ) ∨ {4} |
| Ansikten | 18 |
12 {3} 6 {4} |
| Kanter | 20 | |
| Vertices | 9 | |
| Dubbel | Oktaedrisk pyramid | |
| Symmetrigrupp |
B 3 , [4,3,1], order 48 [4,2,1], order 16 [2,2,1], order 8 |
|
| Egenskaper | konvex , regelbunden ansikte | |
I 4-dimensionell geometri begränsas den kubiska pyramiden av en kub på basen och 6 kvadratiska pyramidceller som möts i spetsen. Eftersom en kub har en cirkumradius dividerad med kantlängd mindre än en, kan de fyrkantiga pyramiderna göras med regelbundna ytor genom att beräkna lämplig höjd.
Bilder
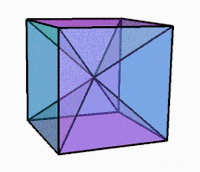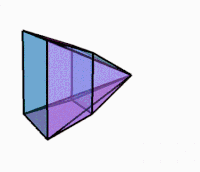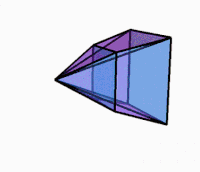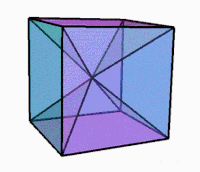 3D-projektion medan du roterar |
Besläktade polytoper och bikakor
Exakt 8 vanliga kubiska pyramider kommer att passa ihop runt en vertex i ett fyrdimensionellt utrymme (toppen av varje pyramid). Denna konstruktion ger en tesserakt med 8 kubiska avgränsande celler, som omger en central vertex med 16 kantlängds långa radier. Tesserakten tesserar 4-dimensionellt utrymme som den tesseraktiska honungskakan . Det 4-dimensionella innehållet i en tesserakt med enhetlig kantlängd är 1, så innehållet i den vanliga kubiska pyramiden är 1/8.
Den vanliga 24-cellen har kubiska pyramider runt varje vertex. Att placera 8 kubiska pyramider på de kubiska gränsande cellerna i en tesserakt är Gossets konstruktion av 24-cellen. Således är 24-cellen konstruerad av exakt 16 kubiska pyramider. Den 24-celliga tesslar ett 4-dimensionellt utrymme som en 24-cells honungskaka .
Dualen till den kubiska pyramiden är en oktaedrisk pyramid , sedd som en oktaedrisk bas, och 8 regelbundna tetraedrar som möts vid en spets.
En kubisk pyramid med höjd noll kan ses som en kub uppdelad i 6 kvadratiska pyramider tillsammans med mittpunkten. Dessa fyrkantiga pyramidfyllda kuber kan tessellate tredimensionellt utrymme som en dual av den trunkerade kubiska honeycomb , kallad en hexakis cubic honeycomb , eller pyramidille .
externa länkar
- Olshevsky, George. "Pyramid" . Ordlista för Hyperspace . Arkiverad från originalet den 4 februari 2007.
- Klitzing, Richard. "4D Segmentotoper" . Klitzing, Richard. "Segmentotop cubpy, K-4.26" .
- Richard Klitzing, Axial-Symmetrical Edge Facets of Uniform Polyhedra
