Normal sannolikhetsplot
Det normala sannolikhetsdiagrammet är en grafisk teknik för att identifiera väsentliga avvikelser från normalitet . Detta inkluderar identifiering av extremvärden , skevhet , kurtosis , behov av transformationer och blandningar . Normala sannolikhetsdiagram är gjorda av rådata, residualer från modellanpassningar och uppskattade parametrar.
I en normal sannolikhetsplot (även kallad en "normal plot") plottas den sorterade datan vs. värden som väljs för att få den resulterande bilden att se nära en rät linje om data är ungefär normalfördelade. Avvikelser från en rät linje tyder på avvikelser från normalitet. Plotten kan utföras manuellt genom att använda ett speciellt rutat papper , kallat normalt sannolikhetspapper . Med moderna datorer görs vanligen vanliga plotter med mjukvara.
Normalsannolikhetsdiagrammet är ett specialfall av Q–Q- sannolikhetsdiagrammet för en normalfördelning. De teoretiska kvantilerna väljs i allmänhet för att approximera antingen medelvärdet eller medianen för motsvarande ordningsstatistik .
Definition
Det normala sannolikhetsdiagrammet bildas genom att plotta den sorterade datan mot en approximation till medelvärdena eller medianerna för motsvarande ordningsstatistik ; se rankit . Vissa plottar data på den vertikala axeln; andra plottar data på den horisontella axeln.
Olika källor använder lite olika uppskattningar för rankits . Formeln som används av funktionen "qqnorm" i det grundläggande "stats"-paketet i R (programmeringsspråk) är följande:
för i = 1, 2, ..., n , där
-
a = 3/8 om n ≤ 10 och
- 0,5 för n > 10,
och Φ −1 är standard normalkvantilfunktionen .
Om uppgifterna överensstämmer med ett urval från en normalfördelning bör punkterna ligga nära en rät linje. Som referens kan en rät linje anpassas till punkterna. Ju längre punkterna varierar från denna linje, desto större indikation på avvikelse från normalitet. Om provet har medelvärde 0, standardavvikelse 1 kan en linje genom 0 med lutning 1 användas.
Med fler poäng blir slumpmässiga avvikelser från en linje mindre uttalade. Normala plotter används ofta med så få som 7 poäng, t.ex. med att plotta effekterna i en mättad modell från ett 2-nivås fraktionellt faktoriellt experiment . Med färre poäng blir det svårare att skilja mellan slumpmässig variabilitet och en väsentlig avvikelse från normalitet.
Andra distributioner
Sannolikhetsdiagram för andra fördelningar än normalen beräknas på exakt samma sätt. Normalkvantilfunktionen Φ −1 ersätts helt enkelt av den önskade fördelningens kvantilfunktion. På så sätt kan ett sannolikhetsdiagram enkelt genereras för vilken fördelning som helst för vilken man har kvantilfunktionen.
Med en platsskalafamilj av distributioner kan fördelningens läge och skalparametrar uppskattas från skärningen och linjens lutning . För andra fördelningar måste parametrarna först uppskattas innan en sannolikhetsplott kan göras.
Tomttyper
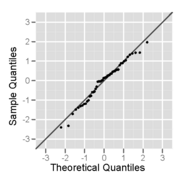
Detta är ett urval av storlek 50 från en normalfördelning, plottad som både ett histogram och en normal sannolikhetsplot.
Normal sannolikhetsplot av ett urval från en normalfördelning – det ser ganska rakt ut, åtminstone när de få stora och små värdena ignoreras.
Histogram av ett prov från en normalfördelning – det ser ganska symmetriskt och unimodalt ut
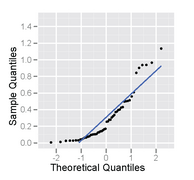
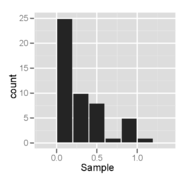
Detta är ett urval av storlek 50 från en höger-skev fördelning, plottad som både ett histogram och en normal sannolikhetsplot.
Normal sannolikhetsplot av ett urval från en höger-snedfördelning – det har en inverterad C-form.
Histogram av ett prov från en höger-snedfördelning – det ser unimodalt ut och snett rätt.
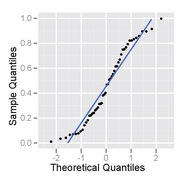
Detta är ett urval av storlek 50 från en enhetlig fördelning, plottad som både ett histogram och en normal sannolikhetsplot.
Normal sannolikhetsplot för ett prov från en enhetlig fördelning – det har en S-form.
Histogram av ett prov från en enhetlig fördelning – det ser multimodalt ut och förmodas ungefär symmetriskt.
Se även
Den här artikeln innehåller material som är allmän egendom från National Institute of Standards and Technology .
Vidare läsning
- Chambers, John; William Cleveland; Beat Kleiner; Paul Tukey (1983). Grafiska metoder för dataanalys . Wadsworth.
externa länkar
- Engineering Statistics Handbook: Normal Probability Plot
- Statit Support: Testning för "Near-Normality": Probability Plot