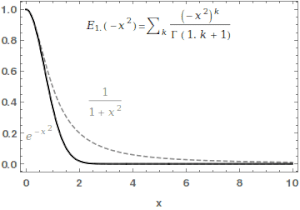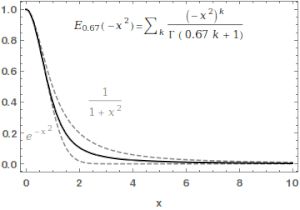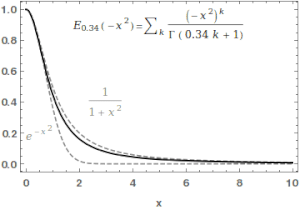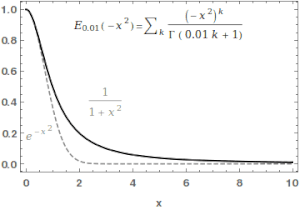
Mittag-Leffler funktion

Mittag-Leffler-funktionen kan användas för att interpolera kontinuerligt mellan en Gaussisk och en Lorentzisk funktion.

Inom matematiken är Mittag -Leffler-funktionen $E_{\alpha ,\beta }$ en specialfunktion , en komplex funktion som beror på två komplexa parametrar $\alpha$ och $\beta$ . Det kan definieras av följande serie när den verkliga delen av $\alpha$ är strikt positiv:

E_{\alpha ,\beta }(z)=\summa _{k=0}^{\infty } {\frac {z^{k}}{\Gamma (\alpha k+\beta )}},

där $\Gamma (x)$ är gammafunktionen . När $\beta =1$ förkortas det till $E_{\alpha }(z)=E_{\alpha ,1}( z)$ . För $\alpha =0$ är serien ovan lika med Taylor-expansionen av den geometriska serien och följaktligen $E_{0,\beta }(z)={\frac {1}{\Gamma (\beta )}}{\frac {1}{1-z}}$ .

I fallet $\alpha$ och $\beta$ är reella och positiva, konvergerar serien för alla värden av argumentet $z$ , så Mittag-Leffler-funktionen är en hel funktion . Denna funktion är uppkallad efter Gösta Mittag-Leffler . Denna klass av funktioner är viktiga i teorin om bråkräkningen .

För ${\displaystyle \alpha >0} är$ Mittag-Leffler-funktionen $E_{\alpha ,1}(z)$ en hel funktion av ordningen $1/\alpha$ , och är i någon mening den enklaste hela funktionen i sin ordning.

Mittag-Leffler-funktionen uppfyller recurrence-egenskapen (sats 5.1 av )

E_{\alpha ,\beta }(z)={\frac {1} {z}}E_{\alpha ,\beta -\alpha }(z)-{\frac {1}{z\Gamma (\beta -\alpha )}},

från vilken Poincarés asymptotiska expansion

E_{\alpha ,\beta }(z)\sim -\sum _{k=1}{\ frac {1}{z^{k}\Gamma (\beta -k\alpha )}}

följer, vilket är sant för $z\to -\infty$ .

Speciella fall

För $\alpha =0,1/2,1,2$ finner vi: (avsnitt 2 av )

Felfunktion :

E_{\frac {1}{2}}(z)=\exp(z^{2})\operatörsnamn {erfc} (-z).

Summan av en geometrisk progression :

E_{0}(z)=\sum _{k=0}^{\infty }z^{k}={\frac {1}{1-z}},\,|z |<1.

Exponentiell funktion :

E_{1}(z)=\summa _{k=0}^{\infty }{\frac {z^{k}}{\Gamma (k+1)}}=\summa _{k =0}^{\infty }{\frac {z^{k}}{k!}}=\exp(z).

Hyperbolisk cosinus :

E_{2}(z)=\cosh({\sqrt {z}}),{\text{ och }}E_{2}(-z^{2})=\cos(z).

För $\beta =2$ har vi

E_{1,2}(z)={\frac {e^{z}-1}{z}},

E_{2,2}(z)={\frac {\sinh({\sqrt {z}})}{\sqrt {z}}}.

För $\alpha =0,1,2$ , integralen

\int _{0}^{z}E_{\alpha }(-s^{2})\,{\mathrm {d} }s

ger respektive: $\arctan(z)$ , ${\tfrac {\sqrt {\pi }}{2}}\operatörsnamn {erf} ( z)$ , $\sin(z)$ .

Mittag-Lefflers integrerade representation

Den integrerade representationen av Mittag-Leffler-funktionen är (avsnitt 6 av )

E_{\alpha ,\beta } (z)={\frac {1}{2\pi i}}\oint _{C}{\frac {t^{\alpha -\beta}e^{t}}{t^{\alpha}- z}}\,dt,\Re (\alpha )>0,\Re (\beta )>0,

där konturen $C$ börjar och slutar på $-\infty$ och cirklar runt integrandens singulariteter och grenpunkter.

Relaterat till Laplace-transformen och Mittag-Leffler-summeringen är uttrycket (Ekv (7.5) av med $m=0$ )

\int _{0}^{\infty }e^{-tz}t^{\beta -1}E_{\alpha ,\beta }(\pm r\,t^{\alpha }) \,dt={\frac {z^{\alpha -\beta }}{z^{\alpha }\mp r}},\Re (z)>0,\Re (\alpha )>0,\Re (\beta )>0.

Tillämpningar av Mittag-Leffler-funktionen

En av tillämpningarna för Mittag-Leffler-funktionen är att modellera viskoelastiska material i fraktionerad ordning. Experimentella undersökningar av det tidsberoende relaxationsbeteendet hos viskoelastiska material kännetecknas av en mycket snabb minskning av spänningen i början av relaxationsprocessen och en extremt långsam avklingning under stora tider. Det kan till och med ta lång tid innan ett konstant asymptotiskt värde uppnås. Därför krävs många Maxwell-element för att beskriva avslappningsbeteende med tillräcklig noggrannhet. Detta slutar i ett svårt optimeringsproblem för att identifiera ett stort antal materialparametrar. Å andra sidan har begreppet fraktionerade derivat under åren introducerats till teorin om viskoelasticitet . Bland dessa modeller visade sig den fraktionerade Zener- modellen vara mycket effektiv för att förutsäga den dynamiska naturen hos gummiliknande material med endast ett litet antal materialparametrar. Lösningen av motsvarande konstitutiva ekvation leder till en relaxationsfunktion av typen Mittag-Leffler. Den definieras av potensserien med negativa argument. Denna funktion representerar alla väsentliga egenskaper hos avslappningsprocessen under påverkan av en godtycklig och kontinuerlig signal med ett hopp vid utgången.

Se även

Anteckningar

R -paket 'MittagLeffleR' av Gurtek Gill, Peter Straka. Implementerar Mittag-Leffler-funktionen, distribution, generering av slumpmässiga variationer och uppskattning.

Mittag-Leffler, MG: Sur la nouvelle fonction E(x). CR Acad. Sci. Paris 137, 554–558 (1903)
Mittag-Leffler, MG: Sopra la funzione E˛.x/. Rämna. R. Enl. Lincei, (Ser. 5) 13, 3–5 (1904)
Gorenflo R., Kilbas AA, Mainardi F., Rogosin SV, Mittag-Leffler Funktioner, relaterade ämnen och tillämpningar (Springer, New York, 2014) 443 sidor ISBN 978-3-662-43929-6
Igor Podlubny (1998). "kapitel 1". Bråk-differentialekvationer. En introduktion till bråk-derivat, bråk-differentialekvationer, några metoder för deras lösning och några av deras tillämpningar . Matematik i naturvetenskap och teknik. Akademisk press. ISBN 0-12-558840-2 .
Kai Diethelm (2010). "kapitel 4". Analysen av bråk-differentialekvationer: en tillämpningsorienterad exponering med differentialoperatorer av Caputo-typ . Föreläsningsanteckningar i matematik. Heidelberg och New York: Springer-Verlag. ISBN 978-3-642-14573-5 .

externa länkar

Den här artikeln innehåller material från Mittag-Leffler-funktionen på PlanetMath , som är licensierad under Creative Commons Attribution/Dela Lika-licensen .