Maximal effektöverföringssats

Inom elektroteknik säger satsen för maximal effektöverföring att, för att erhålla maximal extern effekt från en strömkälla med intern resistans , måste belastningens resistans vara lika med källans resistans sett från dess utgångsterminaler . Moritz von Jacobi publicerade satsen för maximal effekt (överföring) omkring 1840; den kallas också för " Jakobis lag ".

Satsen resulterar i maximal effektöverföring från kraftkällan till lasten, och inte maximal effektivitet av användbar effekt av den totala förbrukade energin . Om belastningsresistansen görs större än källresistansen ökar effektiviteten (eftersom en högre procentandel av källeffekten överförs till belastningen), men storleken på belastningseffekten minskar (eftersom den totala kretsresistansen ökar). Om belastningsmotståndet görs mindre än källmotståndet, minskar effektiviteten (eftersom det mesta av strömmen slutar att försvinna i källan). Även om den totala energiförlusten ökar (på grund av ett lägre totalmotstånd), minskar mängden som förbrukas i lasten.

Satsen anger hur man väljer (för att maximera kraftöverföringen) belastningsresistansen, när källresistansen är given. Det är en vanlig missuppfattning att tillämpa satsen i det motsatta scenariot. Det inte hur man väljer källmotstånd för ett givet belastningsmotstånd. Faktum är att källresistansen som maximerar kraftöverföringen från en spänningskälla alltid är noll (den hypotetiska ideala spänningskällan ), oavsett värdet på belastningsresistansen.

Satsen kan utvidgas till växelströmskretsar som inkluderar reaktans och anger att maximal effektöverföring sker när belastningsimpedansen är lika med det komplexa konjugatet av källimpedansen.

Teoremets matematik gäller även andra fysiska interaktioner, såsom:

• mekaniska kollisioner mellan två föremål,
• laddningsdelning mellan två kondensatorer,
• vätskeflöde mellan två cylindrar,
• överföring och reflektion av ljus vid gränsen mellan två medier.

Maximerar kraftöverföring kontra energieffektivitet

Förenklad modell för att driva en last med resistans RL _V av en källa med spänning S _och resistans RS _.

Satsen missförstods ursprungligen (särskilt av Joule ) för att antyda att ett system bestående av en elmotor som drivs av ett batteri inte kunde vara mer än 50 % effektiv , eftersom den effekt som försvinner som värme i batteriet alltid skulle vara lika med den levererade effekten till motorn när impedanserna matchades.

År 1880 visades detta antagande vara falskt av antingen Edison eller hans kollega Francis Robbins Upton , som insåg att maximal effektivitet inte var detsamma som maximal kraftöverföring.

För att uppnå maximal effektivitet kan resistansen hos källan (oavsett om det är ett batteri eller en dynamo ) göras (eller bör) göras så nära noll som möjligt. Med hjälp av denna nya förståelse fick de en verkningsgrad på cirka 90% och bevisade att elmotorn var ett praktiskt alternativ till värmemotorn .

Den röda kurvan visar effekten i lasten, normaliserad i förhållande till dess maximalt möjliga. Den svarta kurvan visar verkningsgraden η .

Verkningsgraden η är förhållandet mellan RS _effekt RL _som förbrukas av belastningsresistansen RL _för och total effekt som förbrukas av kretsen (vilket inkluderar spänningskällans resistans såväl som ) :

$$\eta ={\frac {P_{\mathrm {L} }}{P_{\mathrm {Totalt} }}}={\frac {I^{2}\cdot R_{\mathrm {L} } }{I^{2}\cdot (R_{\mathrm {L} }+R_{\mathrm {S} })}}={\frac {R_{\mathrm {L} }}{R_{\mathrm { L} }+R_{\mathrm {S} }}}={\frac {1}{1+R_{\mathrm {S} }/R_{\mathrm {L} }}}\,.$$

Tänk på tre särskilda fall:

• Om ${\displaystyle R_{\mathrm {L} }/R_{\mathrm {S} }\to 0} ,$ då $\eta \to 0.$ Effektiviteten närmar sig 0 % om belastningsmotståndet närmar sig noll (en kortslutning ), eftersom all ström förbrukas i källan och ingen ström förbrukas i kortslutningen. Observera att spänningskällor måste ha visst motstånd.
• Om $R_{\mathrm {L} }/R_{\mathrm {S} }=1$ så är $\eta ={\tfrac {1}{2}}.$ Verkningsgraden är endast 50 % om belastningsresistansen är lika med källresistansen (vilket är villkoret för maximal effektöverföring).
• Om ${\displaystyle R_{\mathrm {L} }/R_{\mathrm {S} }\to \infty } ,$ då $\eta \to 1.$ Effektivitet närmar sig 100 % om belastningsresistansen närmar sig oändligheten (även om den totala effektnivån tenderar mot noll) eller om källresistansen närmar sig noll. Att använda ett stort förhållande kallas impedansbryggning .

Impedansmatchning

Huvudartikel: impedansmatchning

Ett relaterat koncept är reflektionsfri impedansmatchning .

I radiofrekvensöverföringsledningar och annan elektronik finns det ofta ett krav att matcha källimpedansen (vid sändaren) till belastningsimpedansen ( som en antenn ) för att undvika reflektioner i överföringsledningen som kan överbelasta eller skada sändaren.

Kalkylbaserat bevis för rena resistiva kretsar

I den förenklade modellen för att driva en belastning med resistans R _L av en källa med spänning V _S och källresistans R _{S , är} den resulterande strömmen I enligt Ohms lag helt enkelt källspänningen dividerad med den totala kretsresistansen:

$$I={\frac {V_{S}}{R_{\mathrm {S} }+R_{\mathrm {L} }}}.$$

Effekten P _L som förbrukas i lasten är kvadraten på strömmen multiplicerat med motståndet:

$$P_{\mathrm {L} }=I^{2}R_{\mathrm {L} }=\left({\frac {V_{S}}{R_{\mathrm {S}}+R_{ \mathrm {L} }}}\right)^{2}R_{\mathrm {L} }={\frac {V_{S}^{2}}{R_{\mathrm {S} }^{2} /R_{\mathrm {L} }+2R_{\mathrm {S} }+R_{\mathrm {L} }}}.$$

Värdet på R _L för vilket detta uttryck är ett maximum skulle kunna beräknas genom att differentiera det, men det är lättare att beräkna värdet på R _L för vilket nämnaren

$$R_{\mathrm {S} }^{2}/R_{\mathrm {L} }+2R_{\mathrm {S} }+R_{\ mathrm {L} }$$

är ett minimum. Resultatet blir detsamma i båda fallen. Differentiering av nämnaren med avseende på R _L :

$${\frac {d}{dR_{\mathrm {L} }} }\left(R_{\mathrm {S} }^{2}/R_{\mathrm {L}}+2R_{\mathrm {S} }+R_{\mathrm {L} }\right)=-R_{ \mathrm {S} }^{2}/R_{\mathrm {L} }^{2}+1.$$

För ett maximum eller minimum är den första derivatan noll, alltså

$$R_{\mathrm {S} }^{2}/R_{\mathrm {L} }^{2}=1$$

eller

$$R_{\mathrm {L} }=\pm R_{\mathrm {S} }.$$

I praktiska resistiva kretsar är RS _. och R _L båda positiva, så det positiva tecknet i ovanstående är den korrekta lösningen

För att ta reda på om denna lösning är ett minimum eller ett maximum, differentieras nämnaruttrycket igen:

$${\frac {d^{2}}{dR_{\mathrm {L} }^{2}}}\left({R_{\mathrm {S} }^{2}/R_{\mathrm { L} }+2R_{\mathrm {S} }+R_{\mathrm {L} }}\right)={2R_{\mathrm {S} }^{2}}/{R_{\mathrm {L} } ^{3}}.$$

Detta är alltid positivt för positiva värden för $R_{\mathrm {S} }$ och ${\displaystyle R_{\mathrm {L} }} ,$ vilket visar att nämnaren är ett minimum, och potensen är därför ett maximum, när

$$R_{\mathrm {S} }=R_{\mathrm {L} }.$$

Ovanstående bevis antar fast resistans $R_{\mathrm {S} }$ . När källresistansen kan varieras kan den effekt som överförs till lasten ökas genom att minska $R_{\textrm {S}}$ . Till exempel kommer en 100 volts källa med en $R_{\textrm {S}}$ på $10\,\Omega$ leverera 250 watt effekt till en $10\ ,\Omega$ ladda; reducering av $R_{\textrm {S}}$ till $0\,\Omega$ ökar den levererade effekten till 1000 watt.

Observera att detta visar att maximal effektöverföring också kan tolkas som att belastningsspänningen är lika med hälften av Thevenin-spänningsekvivalenten för källan.

I reaktiva kretsar

Effektöverföringssatsen gäller även när källan och/eller lasten inte är rent resistiva.

En förfining av maximieffektsatsen säger att alla reaktiva komponenter av källa och last ska vara av samma storlek men motsatt tecken. ( Se nedan för en härledning. )

• Detta betyder att källan och belastningsimpedanserna bör vara komplexa konjugat av varandra.
• När det gäller rena resistiva kretsar är de två koncepten identiska.

Fysiskt realiserbara källor och belastningar är vanligtvis inte rent resistiva, de har vissa induktiva eller kapacitiva komponenter, och därför finns det faktiskt praktiska tillämpningar av denna sats, under namnet komplex konjugerad impedansmatchning.

Om källan är totalt induktiv (kapacitiv) skulle en totalt kapacitiv (induktiv) belastning, i frånvaro av resistiva förluster, få 100 % av energin från källan men skicka tillbaka den efter en kvarts cykel.

Den resulterande kretsen är inget annat än en resonans LC-krets där energin fortsätter att svänga fram och tillbaka. Denna oscillation kallas reaktiv effekt .

Effektfaktorkorrigering (där en induktiv reaktans används för att "balansera ut" en kapacitiv), är i huvudsak samma idé som komplex konjugerad impedansmatchning även om det görs av helt andra skäl.

För en fast reaktiv källa maximerar maximieffektsatsen den verkliga effekten (P) som levereras till belastningen genom komplex konjugat som matchar belastningen med källan.

För en fast reaktiv belastning minimerar effektfaktorkorrigering den skenbara effekten (S) (och onödig ström) som leds av transmissionsledningarna, samtidigt som samma mängd verklig effektöverföring bibehålls.

Detta görs genom att lägga till en reaktans till lasten för att balansera ut lastens egen reaktans, ändra den reaktiva lastimpedansen till en resistiv lastimpedans.

Bevis

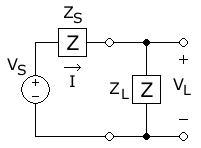
I detta diagram överförs växelström från källan, med spänningens fasstorlek $|V_{\text{S}}|$ (positiv toppspänning) och fast källimpedans $Z_{\text{S}}$ (S för källa), till en belastning med impedans $Z_{\text{L}}$ (L för belastning), vilket resulterar i en (positiv) magnitud $|I|$ av den aktuella fasor $I$ . Denna magnitud $|I|$ resulterar från att dividera storleken på källspänningen med storleken på den totala kretsimpedansen:

$$|I|={|V_{\text{S}}| \over |Z_{\text{S}}+Z_{\text{L}}|}.$$

Medeleffekten $P_{\text{L}}$ som förbrukas i belastningen är kvadraten på strömmen multiplicerat med den resistiva delen (den verkliga delen) $R_{\text{L}}$ av belastningsimpedansen $Z_{\text{L}}$ :

$${\begin{aligned}P_{\text{L}}&=I_{\text{rms}}^{ 2}R_{\text{L}}={1 \över 2}|I|^{2}R_{\text{L}}\\&={1 \över 2}\vänster({|V_{\ text{S}}| \över |Z_{\text{S}}+Z_{\text{L}}|}\right)^{2}R_{\text{L}}={1 \över 2} {|V_{\text{S}}|^{2}R_{\text{L}} \över (R_{\text{S}}+R_{\text{L}})^{2}+( X_{\text{S}}+X_{\text{L}})^{2}},\end{aligned}}$$

där $R_{\text{S}}$ och $R_{\text{L}}$ anger resistanserna, det vill säga de reella delarna, och $X_{\text {S}}$ och $X_{\text{L}}$ betecknar reaktanserna, det vill säga de imaginära delarna, för käll- och belastningsimpedanserna $Z_{\text{S}}$ och $Z_{\text{L}}$ .

För att bestämma, för en given källspänning $V_{\text{S}}$ och impedans $Z_{\text{S}},$ värdet på lastimpedansen ${ \displaystyle Z_{\text{L}},}$ för vilket detta uttryck för potensen ger ett maximum, hittar man först, för varje fixerat positivt värde på $R_{\text{L}}$ , värdet av den reaktiva termen $X_{\text{L}}$ för vilken nämnaren

$$(R_{\text{S}}+R_{\text{L}})^{2}+(X_{\text{ S}}+X_{\text{L}})^{2}$$

är ett minimum. Eftersom reaktanser kan vara negativa uppnås detta genom att anpassa belastningsreaktansen till

$$X_{\text{L}}=-X_{\text{S}}.$$

Detta reducerar ovanstående ekvation till:

$$P_{\text{L}}={\frac {1}{2}}{\frac {|V_{\text{S}}|^{2 }R_{\text{L}}}{(R_{\text{S}}+R_{\text{L}})^{2}}}$$

och det återstår att hitta värdet på $R_{\text{L}}$ som maximerar detta uttryck. Detta problem har samma form som i det rent resistiva fallet, och det maximerande villkoret är därför $R_{\text{L}}=R_{\text{S}}.$

De två maximerande villkoren

• $R_{\text{L}}=R_{\text{S}}$
• $X_{\text{L}}=-X_{\text{S}}$

beskriv det komplexa konjugatet av källimpedansen, betecknad med $^{*},$ och kan således koncist kombineras till:

$$Z_{\text{L}}=Z_{\text{S}}^{*}.$$

Anteckningar

• HW Jackson (1959) Introduktion till elektroniska kretsar, Prentice-Hall.

externa länkar

• Konjugerad matchning kontra reflektionsfri matchning ( PDF ) hämtad från elektromagnetiska vågor och antenner
• Gnistsändaren. 2. Maximera kraften, del 1.