Magnetresistens

Magnetoresistans är tendensen hos ett material (ofta ferromagnetiskt ) att ändra värdet på dess elektriska resistans i ett externt applicerat magnetfält . Det finns en mängd olika effekter som kan kallas magnetresistens. Vissa förekommer i icke-magnetiska bulkmetaller och halvledare, såsom geometrisk magnetoresistans, Shubnikov-de Haas-svängningar eller den vanliga positiva magnetoresistansen i metaller. Andra effekter uppstår i magnetiska metaller, såsom negativ magnetoresistans i ferromagneter eller anisotrop magnetoresistans (AMR). Slutligen, i flerkomponent- eller flerskiktssystem (t.ex. magnetiska tunnelövergångar), jättemagnetoresistans (GMR), tunnelmagnetoresistans (TMR), kolossal magnetoresistans (CMR) och extraordinär magnetoresistans (EMR) observeras.

Den första magnetoresistiva effekten upptäcktes 1856 av William Thomson , mer känd som Lord Kelvin, men han kunde inte sänka det elektriska motståndet för någonting med mer än 5%. Idag är system inklusive halvmetaller och koncentriska ring- EMR -strukturer kända. I dessa kan ett magnetfält justera motståndet i storleksordningar. Eftersom olika mekanismer kan förändra resistansen är det användbart att separat överväga situationer där det beror på ett magnetiskt fält direkt (t.ex. geometrisk magnetoresistans och multiband magnetoresistans) och de där det gör det indirekt genom magnetisering (t.ex. AMR och TMR ) .

Upptäckt

William Thomson (Lord Kelvin) upptäckte vanlig magnetoresistans första gången 1856. Han experimenterade med järnbitar och upptäckte att motståndet ökar när strömmen är i samma riktning som den magnetiska kraften och minskar när strömmen är 90° mot den magnetiska kraften . Han gjorde sedan samma experiment med nickel och fann att det påverkades på samma sätt men effekten var större. Denna effekt kallas anisotropisk magnetoresistans (AMR).

Animation om grafer relaterade till upptäckten av jättemagnetoresistans .

Corbino skiva. Med magnetfältet avstängt flyter en radiell ström i den ledande ringen på grund av batteriet anslutet mellan de (oändliga) ledningsfälgarna. När ett magnetfält längs axeln slås på (B pekar direkt ut från skärmen) Lorentz-kraften en cirkulär komponent av ström, och motståndet mellan den inre och yttre kanten går upp. Denna ökning av motståndet på grund av magnetfältet kallas magnetoresistans .

2007 tilldelades Albert Fert och Peter Grünberg tillsammans Nobelpriset för upptäckten av jättemagnetoresistans .

Geometrisk magnetoresistans

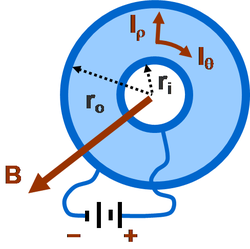
Ett exempel på magnetoresistens på grund av direkt inverkan av magnetfält på elektrisk ström kan studeras på en Corbino-skiva (se figur). Den består av en ledande ring med perfekt ledande fälgar. Utan magnetfält driver batteriet en radiell ström mellan fälgarna. När ett magnetiskt fält vinkelrätt mot ringens plan appliceras (antingen in i eller ut ur sidan) flödar också en cirkulär komponent av ström, på grund av Lorentz-kraften . Det initiala intresset för detta problem började med Boltzmann 1886 och granskades självständigt av Corbino 1911.

I en enkel modell, om man antar att svaret på Lorentzkraften är detsamma som för ett elektriskt fält, ges bärarhastigheten v av:

\mathbf {v} =\mu \left(\mathbf {E} +\mathbf {v\times B} \right),\

där μ är bärarens rörlighet. När vi löser hastigheten finner vi:

\mathbf {v} ={\frac {\mu }{1+(\mu B)^{2}}}\left(\mathbf {E} +\mu \mathbf {E\times B} + \mu ^{2}(\mathbf {B\cdot E} )\mathbf {B} \right)={\frac {\mu}{1+(\mu B)^{2}}}\left(\ mathbf {E} _{\perp }+\mu \mathbf {E\times B} \right)+\mu \mathbf {E} _{\parallel },\

där den effektiva minskningen av rörligheten på grund av B -fältet (för rörelse vinkelrätt mot detta fält) är uppenbar. Elektrisk ström (proportionell mot den radiella hastighetskomponenten) kommer att minska med ökande magnetfält och därför kommer enhetens motstånd att öka. Kritiskt sett beror detta magnetoresistiva scenario känsligt på enhetens geometri och strömlinjer och det är inte beroende av magnetiska material.

I en halvledare med enkelbärartyp är magnetoresistansen proportionell mot (1 + ( μB ) ² ), där μ är halvledarmobiliteten (enheter m ² ·V ⁻¹ ·s ⁻¹ eller T ⁻¹ ) och B är magnetfält (enheter teslas ). Indiumantimonid , ett exempel på en halvledare med hög rörlighet, skulle kunna ha en elektronmobilitet över 4 m ² ·V ⁻¹ ·s ⁻¹ vid 300 K. Så i ett 0,25 T-fält skulle till exempel magnetoresistansökningen vara 100 %.

Anisotropisk magnetoresistans (AMR)

Motståndet hos en tunn Permalloy- film visas här som en funktion av vinkeln på ett applicerat yttre fält.

Thomsons experiment är ett exempel på AMR, en egenskap hos ett material där ett beroende av elektriskt motstånd på vinkeln mellan den elektriska strömriktningen och magnetiseringsriktningen observeras . Effekten uppstår från den samtidiga verkan av magnetisering och spin-omloppsinteraktion och dess detaljerade mekanism beror på materialet. Det kan till exempel bero på en större sannolikhet för sd-spridning av elektroner i magnetiseringsriktningen (som styrs av det applicerade magnetfältet). Nettoeffekten (i de flesta material) är att det elektriska motståndet har maximalt värde när strömriktningen är parallell med det pålagda magnetfältet. AMR av nya material undersöks och magnituder upp till 50 % har observerats i vissa ferromagnetiska uranföreningar.

I polykristallina ferromagnetiska material kan AMR endast bero på vinkeln $\varphi =\psi -\theta$ mellan magnetiseringen och strömriktningen och (så länge som materialets resistivitet kan beskrivas med en rank-två-tensor), måste den följa

$\rho (\varphi )=\rho _{\perp }+(\rho _{\parallel }-\rho _{ \perp })\cos ^{2}\varphi$

där ${\displaystyle \rho } är$ filmens (längsgående) resistivitet och $\rho _{\parallel ,\perp }$ är resistiviteterna för $\varphi =0$ och $90^{\circ }$ , respektive. I samband med longitudinell resistivitet finns det också transversal resistivitet som kallas (något förvirrande [ 1] ) den plana Hall-effekten. I monokristaller beror resistiviteten $\rho$ också på $\psi ,\theta$ individuellt.

För att kompensera för de icke-linjära egenskaperna och oförmågan att detektera polariteten hos ett magnetfält, används följande struktur för sensorer. Den består av ränder av aluminium eller guld placerade på en tunn film av permalloy (ett ferromagnetiskt material som uppvisar AMR-effekten) som lutar i en vinkel på 45°. Denna struktur tvingar strömmen att inte flyta längs de "enkla axlarna" av tunn film, utan i en vinkel på 45°. Resistansberoendet har nu en permanent offset som är linjär runt nollpunkten. På grund av sitt utseende kallas denna sensortyp för " frisörstolpe ".

AMR-effekten används i ett brett spektrum av sensorer för mätning av jordens magnetfält (elektronisk kompass ), för mätning av elektrisk ström (genom att mäta det magnetiska fält som skapas runt ledaren), för trafikdetektering och för linjär position och vinkelavkänning. De största AMR-sensortillverkarna är Honeywell , NXP Semiconductors , STMicroelectronics och Sensitec GmbH .

Som teoretiska aspekter härledde IA Campbell, A. Fert och O. Jaoul (CFJ) ett uttryck för AMR-förhållandet för Ni-baserade legeringar med hjälp av tvåströmsmodellen med ss- och sd-spridningsprocesser, där s är en ledningselektron och d är 3d-tillstånd med spin-omloppsinteraktionen. AMR-förhållandet uttrycks som

${\frac {\Delta \rho }{\rho }}={\frac {\rho _{\parallel }-\ rho _{\perp }}{\rho _{\perp }}}=\gamma (\alpha -1),$

med $\gamma =(3/4)(A/H)^{2}$ och $\alpha =\ rho _{\downarrow }/\rho _{\uparrow }$ , där $A$ , $H$ och $\rho _{\sigma }$ är en spin-omloppsbana kopplingskonstant (s.k. $\zeta$ ), ett utbytesfält respektive en resistivitet för spin $\sigma$ . Dessutom har nyligen Satoshi Kokado et al. har erhållit det allmänna uttrycket av AMR-förhållandet för 3d-övergångsmetallferromagneter genom att utöka CFJ-teorin till en mer allmän. Det allmänna uttrycket kan även appliceras på halvmetaller.

Se även

Fotnoter

1. Den (vanliga) Hall-effekten ändrar tecken vid magnetfältomkastning och det är en orbital effekt (ej relaterad till spinn) på grund av Lorentz-kraften. Transversal AMR (planar Hall-effekt) ändrar inte tecken och det orsakas av spin-orbit interaktion .

^ Pippard, AB (1989). Magnetresistens i metaller . Cambridge University Press. ISBN 978-0-521-32660-5 .
^ Coleman husbil; Isin, A. (1966), "Magnetoresistance in Iron Single Crystals", Journal of Applied Physics , 37 (3): 1028–9, Bibcode : 1966JAP....37.1028C , doi : 10.1063/1.1708320
^ "Ostoppbar magnetomotstånd" .
^ ^a ^b Thomson, W. (18 juni 1857), "Om de elektrodynamiska egenskaperna hos metaller: - Effekter av magnetisering på den elektriska konduktiviteten hos nickel och järn", Proc . R. Soc. Lond. , 8 : 546–550, doi : 10.1098/rspl.1856.0144
^ Nobelpriset i fysik 2007 , Nobel Media AB, 9 oktober 2007 , hämtat 25 juni 2014
^ G Giuliani (2008). "En allmän lag för elektromagnetisk induktion". EPL . 81 (6): 60002. arXiv : 1502.00502 . Bibcode : 2008EL.....8160002G . doi : 10.1209/0295-5075/81/60002 . S2CID 14917438 .
^ McGuire, T.; Potter, R. (1975). "Anisotropisk magnetresistans i ferromagnetiska 3d-legeringar" (PDF) . IEEE-transaktioner på magnetik . 11 (4): 1018–38. Bibcode : 1975ITM....11.1018M . doi : 10.1109/TMAG.1975.1058782 .
^ Wiśniewski, P. (2007). "Jätte anisotropisk magnetresistens och magnetotermisk kraft i kubiska 3:4 uranpnictider". Bokstäver i tillämpad fysik . 90 (19): 192106. Bibcode : 2007ApPhL..90s2106W . doi : 10.1063/1.2737904 .
^ De Ranieri, E.; Rushforth, AW; Výborný, K.; Rana, U.; Ahmed, E.; Campion, RP; Foxon, CT; Gallagher, BL; Irvine, AC; Wunderlich, J.; Jungwirth, T. (10 juni 2008), "Litografiskt och elektriskt kontrollerade töjningseffekter på anisotropisk magnetoresistans i (Ga, Mn)As", New J. Phys. , 10 (6): 065003, arXiv : 0802.3344 , Bibcode : 2008NJPh...10f5003D , doi : 10.1088/1367-2630/10/6/06509ID 1 , S192C
^ Campbell, IA; Fert, A.; Jaoul, O. (1970). "Den spontana resistivitetsanisotropin i Ni-baserade legeringar". J. Phys. C . 3 (1S): S95–S101. Bibcode : 1970JPhC....3S..95C . doi : 10.1088/0022-3719/3/1S/310 .
^ Kokado, Satoshi; Tsunoda, Masakiyo; Harigaya, Kikuo; Sakuma, Akimasa (2012). "Anisotropiska magnetoresistanseffekter i Fe, Co, Ni, Fe4N och halvmetallisk ferromagnet: En systematisk analys". J. Phys. Soc. Jpn . 81 (2): 024705–1–17. arXiv : 1111.4864 . Bibcode : 2012JPSJ...81b4705K . doi : 10.1143/JPSJ.81.024705 . S2CID 100002412 .
^ Kokado, Satoshi; Tsunoda, Masakiyo (2013). "Anisotropisk magnetoresistanseffekt: Allmänt uttryck för AMR-förhållande och intuitiv förklaring till tecken på AMR-förhållande". Avancerad materialforskning . 750–752: 978–982. arXiv : 1305.3517 . Bibcode : 2013arXiv1305.3517K . doi : 10.4028/www.scientific.net/AMR.750-752.978 . S2CID 35733115 .
^ Tang, HX; Kawakami, RK; Awschalom, DD; Roukes, ML (mars 2003), "Giant Planar Hall Effect in Epitaxial (Ga,Mn)As Devices" (PDF) , Phys. Rev. Lett. , 90 (10): 107201, Arxiv : Cond-Mat/0210118 , Bibcode : 2003Phrvl..90J7201T , doi : 10.1103/PhysRevLett.90.107201 , PMID 12689027 , S2CID 1485882

[1] Pippard, AB (1989). Magnetresistens i metaller . Cambridge University Press. ISBN 978-0-521-32660-5 .

[Coleman-2] Coleman husbil; Isin, A. (1966), "Magnetoresistance in Iron Single Crystals", Journal of Applied Physics , 37 (3): 1028–9, Bibcode : 1966JAP....37.1028C , doi : 10.1063/1.1708320

[3] "Ostoppbar magnetomotstånd" .

[Kelvin-4] Thomson, W. (18 juni 1857), "Om de elektrodynamiska egenskaperna hos metaller: - Effekter av magnetisering på den elektriska konduktiviteten hos nickel och järn", Proc . R. Soc. Lond. , 8 : 546–550, doi : 10.1098/rspl.1856.0144

[5] Nobelpriset i fysik 2007 , Nobel Media AB, 9 oktober 2007 , hämtat 25 juni 2014

[Giuliani-6] G Giuliani (2008). "En allmän lag för elektromagnetisk induktion". EPL . 81 (6): 60002. arXiv : 1502.00502 . Bibcode : 2008EL.....8160002G . doi : 10.1209/0295-5075/81/60002 . S2CID 14917438 .

[McGuirePotter-7] McGuire, T.; Potter, R. (1975). "Anisotropisk magnetresistans i ferromagnetiska 3d-legeringar" (PDF) . IEEE-transaktioner på magnetik . 11 (4): 1018–38. Bibcode : 1975ITM....11.1018M . doi : 10.1109/TMAG.1975.1058782 .

[Wiśniewski-8] Wiśniewski, P. (2007). "Jätte anisotropisk magnetresistens och magnetotermisk kraft i kubiska 3:4 uranpnictider". Bokstäver i tillämpad fysik . 90 (19): 192106. Bibcode : 2007ApPhL..90s2106W . doi : 10.1063/1.2737904 .

[9] De Ranieri, E.; Rushforth, AW; Výborný, K.; Rana, U.; Ahmed, E.; Campion, RP; Foxon, CT; Gallagher, BL; Irvine, AC; Wunderlich, J.; Jungwirth, T. (10 juni 2008), "Litografiskt och elektriskt kontrollerade töjningseffekter på anisotropisk magnetoresistans i (Ga, Mn)As", New J. Phys. , 10 (6): 065003, arXiv : 0802.3344 , Bibcode : 2008NJPh...10f5003D , doi : 10.1088/1367-2630/10/6/06509ID 1 , S192C

[CFJ-10] Campbell, IA; Fert, A.; Jaoul, O. (1970). "Den spontana resistivitetsanisotropin i Ni-baserade legeringar". J. Phys. C . 3 (1S): S95–S101. Bibcode : 1970JPhC....3S..95C . doi : 10.1088/0022-3719/3/1S/310 .

[Kokado1-11] Kokado, Satoshi; Tsunoda, Masakiyo; Harigaya, Kikuo; Sakuma, Akimasa (2012). "Anisotropiska magnetoresistanseffekter i Fe, Co, Ni, Fe4N och halvmetallisk ferromagnet: En systematisk analys". J. Phys. Soc. Jpn . 81 (2): 024705–1–17. arXiv : 1111.4864 . Bibcode : 2012JPSJ...81b4705K . doi : 10.1143/JPSJ.81.024705 . S2CID 100002412 .

[Kokado2-12] Kokado, Satoshi; Tsunoda, Masakiyo (2013). "Anisotropisk magnetoresistanseffekt: Allmänt uttryck för AMR-förhållande och intuitiv förklaring till tecken på AMR-förhållande". Avancerad materialforskning . 750–752: 978–982. arXiv : 1305.3517 . Bibcode : 2013arXiv1305.3517K . doi : 10.4028/www.scientific.net/AMR.750-752.978 . S2CID 35733115 .

[13] Tang, HX; Kawakami, RK; Awschalom, DD; Roukes, ML (mars 2003), "Giant Planar Hall Effect in Epitaxial (Ga,Mn)As Devices" (PDF) , Phys. Rev. Lett. , 90 (10): 107201, Arxiv : Cond-Mat/0210118 , Bibcode : 2003Phrvl..90J7201T , doi : 10.1103/PhysRevLett.90.107201 , PMID 12689027 , S2CID 1485882