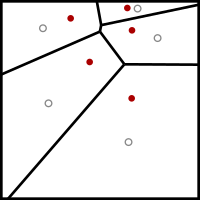
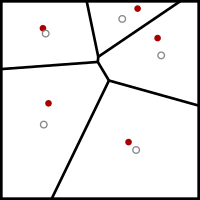
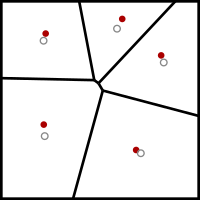
Lloyds algoritm

Inom elektroteknik och datavetenskap är Lloyds algoritm , även känd som Voronoi iteration eller relaxation, en algoritm uppkallad efter Stuart P. Lloyd för att hitta jämnt fördelade uppsättningar av punkter i delmängder av euklidiska rum och partitioner av dessa delmängder till välformade och enhetliga stora konvexa celler. Liksom den närbesläktade k -means-klustringsalgoritmen , hittar den upprepade gånger tyngdpunkten för varje uppsättning i partitionen och delar sedan om ingången enligt vilken av dessa tyngdpunkter som är närmast. I den här inställningen är medeloperationen en integral över ett område av rymden, och den närmaste tyngdpunktsoperationen resulterar i Voronoi-diagram .

Även om algoritmen kan appliceras mest direkt på det euklidiska planet , kan liknande algoritmer också appliceras på högre dimensionella utrymmen eller på utrymmen med andra icke-euklidiska mått. Lloyds algoritm kan användas för att konstruera nära approximationer till centroidala Voronoi-tesselationer av indata, som kan användas för kvantisering , dithering och stippling . Andra tillämpningar av Lloyds algoritm inkluderar utjämning av triangelnät i finita elementmetoden .

Exempel på Lloyds algoritm. Voronoi-diagrammet över aktuella platspositioner (röd) vid varje iteration visas. De grå cirklarna anger tyngdpunkterna i Voronoi-cellerna.

Iteration 1

Iteration 2

Iteration 3

Iteration 15

På den sista bilden är platserna mycket nära Voronoi-cellernas tyngdpunkter. En centroidal Voronoi-tesselation har hittats.

Historia

Algoritmen föreslogs först av Stuart P. Lloyd från Bell Labs 1957 som en teknik för pulskodmodulering . Lloyds verk fick stor spridning men förblev opublicerad till 1982. En liknande algoritm utvecklades oberoende av Joel Max och publicerades 1960, varför algoritmen ibland kallas Lloyd-Max-algoritmen.

Algoritmbeskrivning

Lloyds algoritm börjar med en initial placering av ett antal k punktplatser i ingångsdomänen. I maskutjämnande applikationer skulle dessa vara spetsarna på nätet som ska utjämnas; i andra tillämpningar kan de placeras slumpmässigt eller genom att skära ett enhetligt triangulärt nät av lämplig storlek med ingångsdomänen.

Den utför sedan upprepade gånger följande avslappningssteg:

• Voronoi -diagrammet för k platserna beräknas.
• Varje cell i Voronoi-diagrammet är integrerad och tyngdpunkten beräknas.
• Varje plats flyttas sedan till centrum av dess Voronoi-cell.

Integration och tyngdpunktsberäkning

Eftersom Voronoi-diagramkonstruktionsalgoritmer kan vara mycket icke-triviala, särskilt för ingångar med dimensioner högre än två, kan stegen att beräkna detta diagram och hitta de exakta tyngdpunkterna för dess celler ersättas med en approximation.

Approximation

En vanlig förenkling är att använda en lämplig diskretisering av rymden som ett fint pixel-rutnät, t.ex. texturbufferten i grafikhårdvara. Celler materialiseras som pixlar, märkta med deras motsvarande plats-ID. En cells nya centrum approximeras genom att medelvärdet beräknas för positionerna för alla pixlar som tilldelats samma etikett. Alternativt Monte Carlo-metoder användas, i vilka slumpmässiga provpunkter genereras enligt någon fast underliggande sannolikhetsfördelning, tilldelas den närmaste platsen och medelvärdesberäknas för att approximera tyngdpunkten för varje plats.

Exakt beräkning

Även om inbäddning i andra utrymmen också är möjlig, antar denna utarbetning euklidiskt utrymme med L ^{2 -} normen och diskuterar de två mest relevanta scenarierna, som är två respektive tre dimensioner.

Eftersom en Voronoi-cell har konvex form och alltid omsluter sin plats, finns det triviala nedbrytningar till lättintegrerbara förenklingar:

• I två dimensioner är kanterna på den polygonala cellen anslutna till dess plats, vilket skapar en paraplyformad uppsättning trianglar.
• I tre dimensioner omges cellen av flera plana polygoner som först måste trianguleras:
  • Beräkna ett centrum för polygonytan, t.ex. medelvärdet av alla dess hörn.
  • Att förbinda hörnen på en polygonyta med dess centrum ger en plan paraplyformad triangulering.
  • Trivialt erhålls en uppsättning tetraedrar genom att koppla trianglar av cellens skrov med cellens plats.

Integration av en cell och beräkning av dess tyngdpunkt (massacentrum) ges nu som en viktad kombination av dess simplices centroider (i det följande kallad ${\textstyle \mathbf {c} _{i}} )$ .

• Två dimensioner:
  • För en triangel kan tyngdpunkten lätt beräknas, t.ex. med hjälp av kartesiska koordinater .
  • Viktning beräknas som ytförhållande simplex-till-cell .
• Tre dimensioner:
  • En tetraeders tyngdpunkt finns som skärningspunkten mellan tre bisektorplan och kan uttryckas som en matris-vektorprodukt.
  • volymförhållanden simplex-till-cell .

För en 2D-cell med n triangulära förenklingar och en ackumulerad yta ${\textstil A_{C}=\summa _{i=0}^{n}a_{i}} ($ där ${\textstyle a_{i}}$ är arean av en triangelsimplex ), den nya cellens tyngdpunkt beräknas som:

$C={\frac {1}{A_{C}}}\summa _{i=0}^{n}\mathbf {c} _{ i}a_{i}$

Analogt, för en 3D-cell med volymen ${\textstyle V_{C}=\summa _{i=0}^{n}v_{i}} ($ där ${\ textstyle v_{i}}$ är volymen av en tetraeder simplex), tyngdpunkten beräknas som:

$C={\frac {1}{V_{C}}}\summa _{i=0}^{n}\mathbf {c} _{ i}v_{i}$

Konvergens

Varje gång ett avslappningssteg utförs lämnas punkterna i en något jämnare fördelning: tätt placerade punkter flyttar sig längre ifrån varandra, och punkter som ligger långt ifrån varandra flyttas närmare varandra. I en dimension har denna algoritm visat sig konvergera till ett centroidalt Voronoi-diagram, även kallat en centroidal Voronoi-tesselation . I högre dimensioner är några något svagare konvergensresultat kända.

Algoritmen konvergerar långsamt eller, på grund av begränsningar i numerisk precision, kanske inte konvergerar. Därför slutar verkliga tillämpningar av Lloyds algoritm vanligtvis när distributionen är "tillräckligt bra". Ett vanligt avslutningskriterium är att stoppa när det maximala avståndet som förflyttas av någon plats i en iteration faller under en förinställd tröskel. Konvergensen kan accelereras genom att överavslappna punkterna, vilket görs genom att flytta varje punkt ω gånger avståndet till massans centrum, vanligtvis med ett värde något mindre än 2 för ω .

Ansökningar

Lloyds metod användes ursprungligen för skalär kvantisering, men det är tydligt att metoden sträcker sig även för vektorkvantisering. Som sådan används den flitigt i datakomprimeringstekniker inom informationsteori . Lloyds metod används i datorgrafik eftersom den resulterande fördelningen har blåbrusegenskaper (se även Färger på brus ), vilket betyder att det finns få lågfrekventa komponenter som kan tolkas som artefakter. Den är särskilt väl lämpad för att plocka provpositioner för vibrering . Lloyds algoritm används också för att generera punktritningar i stil med stippling . I den här applikationen kan tyngdpunkterna viktas baserat på en referensbild för att producera stipple illustrationer som matchar en ingångsbild.

I finita elementmetoden delas en indatadomän med en komplex geometri upp i element med enklare former; till exempel är tvådimensionella domäner (antingen delmängder av det euklidiska planet eller ytor i tre dimensioner) ofta uppdelade i trianglar. Det är viktigt för konvergensen av de finita elementmetoderna att dessa element är väl formade; i fallet med trianglar är ofta element som är nästan liksidiga trianglar att föredra. Lloyds algoritm kan användas för att jämna ut ett nät som genereras av någon annan algoritm, flytta dess hörn och ändra anslutningsmönstret mellan dess element för att producera trianglar som är mer liksidiga. Dessa applikationer använder vanligtvis ett mindre antal iterationer av Lloyds algoritm, vilket stoppar den från konvergens, för att bevara andra egenskaper hos nätet, såsom skillnader i elementstorlek i olika delar av nätet. I motsats till en annan utjämningsmetod, Laplacian utjämning (där maskens hörn flyttas till medelvärdet av sina grannars positioner), kan Lloyds algoritm ändra maskans topologi, vilket leder till mer nästan liksidiga element samt undvika problemen med trassel som kan uppstå vid Laplacian utjämning. Laplacian utjämning kan dock appliceras mer allmänt på maskor med icke-triangulära element.

Olika avstånd

Lloyds algoritm används vanligtvis i ett euklidiskt utrymme . Det euklidiska avståndet spelar två roller i algoritmen: det används för att definiera Voronoi-cellerna, men det motsvarar också valet av tyngdpunkten som representativ punkt för varje cell, eftersom tyngdpunkten är den punkt som minimerar det genomsnittliga kvadratiska euklidiska avståndet till punkterna i sin cell. Alternativa avstånd och alternativa centralpunkter än tyngdpunkten kan användas istället. Till exempel Hausner (2001) en variant av Manhattan-metriken (med lokalt varierande orienteringar) för att hitta en sida vid sida av en bild med ungefär kvadratiska brickor vars orientering ligger i linje med egenskaper hos en bild, som han använde för att simulera konstruktionen av kaklade mosaiker . I denna applikation fortsatte Hausner att använda centroider som representativa punkter för sina Voronoi-celler, trots att måttet varierade. Men för mått som skiljer sig mer signifikant från euklidiska, kan det vara lämpligt att välja minimering av medelkvadratavstånd som representativ punkt, istället för tyngdpunkten.

Se även

• Linde –Buzo–Gray-algoritmen , en generalisering av denna algoritm för vektorkvantisering
• längst-först genomgång , en annan metod för att generera jämnt fördelade punkter i geometriska utrymmen
• Mean shift , en relaterad metod för att hitta maxima för en densitetsfunktion
• K-betyder++

externa länkar

• DemoGNG.js Grafisk Javascript-simulator för LBG-algoritm och andra modeller, inkluderar visning av Voronoi-regioner