Lammvågor

Lammvågor fortplantar sig i solida plattor eller sfärer. De är elastiska vågor vars partikelrörelse ligger i det plan som innehåller vågens utbredningsriktning och riktningen vinkelrätt mot plattan. 1917 publicerade den engelske matematikern Horace Lamb sin klassiska analys och beskrivning av akustiska vågor av denna typ. Deras egenskaper visade sig vara ganska komplexa. Ett oändligt medium stöder bara två våglägen som färdas med unika hastigheter; men plattor stöder två oändliga uppsättningar av lammvågslägen, vars hastigheter beror på förhållandet mellan våglängd och platttjocklek.

Sedan 1990-talet har förståelsen och utnyttjandet av lammvågor utvecklats avsevärt, tack vare den snabba ökningen av tillgången på datorkraft. Lambs teoretiska formuleringar har funnit betydande praktisk tillämpning, särskilt inom området oförstörande testning.

Termen Rayleigh-Lamb-vågor omfattar Rayleigh-vågen , en typ av våg som utbreder sig längs en enda yta. Både Rayleigh- och Lamb-vågorna begränsas av de elastiska egenskaperna hos ytan/ytorna som styr dem.

_0
0
Figur 1: Övre respektive nedre: Extensionsläge (S ) med $d/\lambda =0,6$ . Böjningsläge (A ) med $d/\lambda =0,3$ . (Detta är en förenklad grafik. Den är endast baserad på z- komponenten av rörelse, så den återger inte förvrängningen av plattan exakt.)

Lamms karakteristiska ekvationer

I allmänhet styrs elastiska vågor i fasta material av gränserna för de medier där de utbreder sig. Ett tillvägagångssätt för guidad vågutbredning, som ofta används inom fysisk akustik, är att söka sinusformade lösningar på vågekvationen för linjära elastiska vågor som är föremål för randvillkor som representerar den strukturella geometrin. Detta är ett klassiskt egenvärdeproblem .

Vågor i plattor var bland de första styrda vågorna som analyserades på detta sätt. Analysen utvecklades och publicerades 1917 av Horace Lamb , en ledare inom matematisk fysik på sin tid.

Lambs ekvationer härleddes genom att sätta upp formalism för en solid platta med oändlig utsträckning i x- och y -riktningarna och tjocklek d i z -riktningen. Sinusformade lösningar till vågekvationen postulerades, med x- och z-förskjutningar av formen

$\xi =A_{x}f_{x}(z)e^{i(\omega t-kx)} \quad \quad (1)$

$\zeta =A_{z}f_{z}(z)e^{i(\omega t-kx)}\quad \quad (2)$

Denna form representerar sinusformade vågor som utbreder sig i x -riktningen med våglängden 2π/k och frekvensen ω/2π. Förskjutningen är en funktion av endast x , z , t ; det finns ingen förskjutning i y- riktningen och ingen variation av några fysiska storheter i y -riktningen.

Det fysiska gränsvillkoret för plattans fria ytor är att spänningskomponenten i z- riktningen vid z = +/- d /2 är noll. Genom att tillämpa dessa två villkor på de ovan formaliserade lösningarna på vågekvationen kan ett par karakteristiska ekvationer hittas. Dessa är:

${\frac {\tanh(\beta d/2)} {\tanh(\alpha d/2)}}={\frac {4\alpha \beta k^{2}}{(k^{2}+\beta ^{2})^{2}}}\ \quad \quad \quad \quad (3)$

för symmetriska lägen och

${\frac {\tanh(\beta d/2)} {\tanh(\alpha d/2)}}={\frac {(k^{2}+\beta ^{2})^{2}}{4\alpha \beta k^{2}}}\ \quad \quad \quad \quad (4)$

för asymmetriska lägen, där

$\alpha ^{2}=k^{2}-{\frac {\omega ^{2}}{c_{l}^{2}}}\quad \quad {\text{and}}\ quad \quad \beta ^{2}=k^{2}-{\frac {\omega ^{2}}{c_{t}^{2}}}.$

Inneboende i dessa ekvationer är ett samband mellan vinkelfrekvensen ω och vågtalet k. Numeriska metoder används för att hitta fashastigheten c _p = fλ = ω/k och grupphastigheten c _g = dω / dk , som funktioner av d / λ eller fd . cl _{längsgående} och ct _. är de våg- och skjuvvågshastigheterna respektive

Lösningen av dessa ekvationer avslöjar också den exakta formen av partikelrörelsen, som ekvationerna (1) och (2) endast representerar i generisk form. Man har funnit att ekvation (3) ger upphov till en familj av vågor vars rörelse är symmetrisk kring plattans mittplan (planet z = 0), medan ekvation (4) ger upphov till en familj av vågor vars rörelse är antisymmetrisk ca. mellanplanet. Figur 1 visar en medlem i varje familj.

Lambs karakteristiska ekvationer upprättades för vågor som fortplantar sig i en oändlig platta - ett homogent, isotropiskt fast ämne som begränsas av två parallella plan bortom vilka ingen vågenergi kan fortplanta sig. När han formulerade sitt problem begränsade Lamb komponenterna i partikelrörelsen till riktningen för plattans normala ( z -riktning) och riktningen för vågutbredning ( x -riktning). Per definition har lammvågor ingen partikelrörelse i y -riktningen. Rörelse i y -riktningen i plattor finns i de så kallade SH- eller skjuv-horisontella våglägena. Dessa har ingen rörelse i x :et - eller z -riktningar, och är således komplementära till Lamb-vågslägena. Dessa två är de enda vågtyperna som kan fortplanta sig med raka, oändliga vågfronter i en platta enligt definitionen ovan.

Hastighetsspridning som är inneboende i de karakteristiska ekvationerna

Dispersionskurvor för fria lammvågor för två olika Poissons förhållanden $\sigma$ . X-axeln visar produkten av vinkelfrekvensen $\omega$ och plåttjockleken $d$ normaliserad av skjuvvågshastigheten $v_{s}$ . Y-axeln visar fashastigheten $v$ för Lamb-vågen normaliserad av skjuvvågens hastighet. För höga frekvenser $S_{0}$ och $A_{0}$ -lägen har Rayleigh-vågens hastighet, ungefär 92 % av skjuvvågens hastighet.

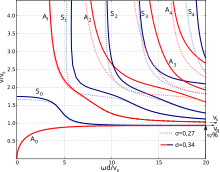
Lammvågor uppvisar hastighetsspridning; det vill säga deras utbredningshastighet c beror på frekvensen (eller våglängden), såväl som på materialets elastiska konstanter och densitet. Detta fenomen är centralt för studien och förståelsen av vågbeteende i plattor. Fysiskt sett är nyckelparametern förhållandet mellan plåttjockleken d och våglängden $\lambda$ . Detta förhållande bestämmer plattans effektiva styvhet och därmed vågens hastighet. I tekniska tillämpningar används en mer praktisk parameter som lätt kan härledas från detta, nämligen produkten av tjocklek och frekvens:

$f\cdot d={\frac {d\cdot c}{\lambda }},$

sedan för alla vågor

$c=f\lambda .$

Förhållandet mellan hastighet och frekvens (eller våglängd) är inneboende i de karakteristiska ekvationerna. När det gäller plattan är dessa ekvationer inte enkla och deras lösning kräver numeriska metoder. Detta var ett svårlöst problem fram till tillkomsten av den digitala datorn fyrtio år efter Lambs ursprungliga verk. Publiceringen av datorgenererade "spridningskurvor" av Viktorov i fd Sovjetunionen, Firestone följt av Worlton i USA, och så småningom många andra förde in lammvågsteorin till den praktiska tillämpningens område. Den kostnadsfria programvaran "Dispersion Calculator" (DC) tillåter beräkning av dispersionsdiagram för isotropa plattor och flerskiktiga anisotropa prover. Experimentella vågformer som observerats i plattor kan förstås genom tolkning med hänvisning till dispersionskurvorna.

Dispersionskurvor - grafer som visar samband mellan våghastighet, våglängd och frekvens i dispersiva system - kan presenteras i olika former. Den form som ger störst insikt i den bakomliggande fysiken har $\omega$ (vinkelfrekvens) på y -axeln och k (vågtal) på x -axeln. Formen som användes av Viktorov, som förde Lamb-vågor till praktisk användning, har våghastighet på y -axeln och $d/\lambda$ , tjocklek/våglängdsförhållandet, på x -axeln. Den mest praktiska formen av alla, för vilken krediten tillskrivs J. och H. Krautkrämer såväl som till Floyd Firestone (som för övrigt myntade frasen "Lamb waves") har våghastighet på y-axeln och fd , den frekvens-tjocklek produkt, på x -axeln.

Lambs karakteristiska ekvationer indikerar existensen av två hela familjer av sinusformade våglägen i oändliga plattor med bredd $d$ . Detta står i kontrast till situationen i obegränsade medier där det bara finns två våglägen, den longitudinella vågen och den tvärgående eller skjuvningsvågen . Liksom i Rayleigh-vågor som utbreder sig längs enstaka fria ytor, är partikelrörelsen i lammvågor elliptisk med sina x och z komponenter beroende på djupet inuti plattan. I en familj av lägen är rörelsen symmetrisk kring mitttjockleksplanet. I den andra familjen är det antisymmetriskt. Fenomenet hastighetsspridning leder till ett rikt utbud av experimentellt observerbara vågformer när akustiska vågor utbreder sig i plattor. Det är cp _{grupphastigheten} cg , _inte den ovan nämnda fashastigheten c eller , som bestämmer moduleringarna som ses i den observerade vågformen. Vågformernas utseende beror kritiskt på det frekvensområde som valts för observation. Böjnings- och förlängningslägena är relativt lätta att känna igen och detta har förespråkats som en teknik för oförstörande testning .

Nollordningens lägen

De symmetriska och antisymmetriska nollordningens lägena förtjänar särskild uppmärksamhet. Dessa lägen har "begynnande frekvenser" på noll. De är alltså de enda moderna som existerar över hela frekvensspektrumet från noll till obestämbart höga frekvenser. I det låga frekvensområdet (dvs. när våglängden är större än plåttjockleken) kallas dessa lägen ofta för "extensionsläget" respektive "böjningsläget", termer som beskriver rörelsens karaktär och de elastiska styvheterna som styr Utbredningshastigheter Den elliptiska partikelrörelsen är huvudsakligen i plattans plan för det symmetriska, förlängningsläget och vinkelrätt mot plattans plan för det antisymmetriska böjningsläget. Dessa egenskaper ändras vid högre frekvenser.

Dessa två lägen är de viktigaste eftersom (a) de finns vid alla frekvenser och (b) i de flesta praktiska situationer bär de mer energi än de högre ordningens lägen.

₀ Den nollordningens symmetriska moden (betecknad S ) färdas med "plåthastigheten" i lågfrekvensregimen där den korrekt kallas "extensionsmoden". I denna regim sträcker sig plattan i utbredningsriktningen och drar ihop sig på motsvarande sätt i tjockleksriktningen. När frekvensen ökar och våglängden blir jämförbar med plåttjockleken börjar böjningen av plåten ha en betydande inverkan på dess effektiva styvhet. Fashastigheten sjunker mjukt medan grupphastigheten sjunker något brant mot ett minimum. Vid ännu högre frekvenser konvergerar både fashastigheten och grupphastigheten mot Rayleigh-våghastigheten - fashastigheten ovanifrån och grupphastigheten underifrån.

I lågfrekvensgränsen för förlängningsläget är z- och x-komponenterna för ytförskjutningen i kvadratur och förhållandet mellan deras amplituder ges av:

$${\frac {a_{z}}{a_{x}}}={\frac {\pi \nu }{(1-\nu )}}.{\frac {d}{\lambda }}$$

där $\nu$ är Poissons förhållande.

₀ Den noll-ordningens antisymmetriska moden (betecknad A ) är mycket spridd i lågfrekvensregimen där den korrekt kallas "böjningsmoden" eller "böjningsmoden". För mycket låga frekvenser (mycket tunna plattor) är både fas- och grupphastigheterna proportionella mot kvadratroten av frekvensen; grupphastigheten är två gånger fashastigheten. Detta enkla förhållande är en konsekvens av förhållandet mellan styvhet och tjocklek för tunna plåtar vid böjning. Vid högre frekvenser där våglängden inte längre är mycket större än plåttjockleken bryts dessa samband. Fashastigheten stiger mindre och mindre snabbt och konvergerar mot Rayleigh-våghastigheten i högfrekvensgränsen. Grupphastigheten passerar genom ett maximum, lite snabbare än skjuvvågshastigheten, när våglängden är ungefär lika med plåttjockleken. Den konvergerar sedan ovanifrån till Rayleigh-våghastigheten i högfrekvensgränsen.

I experiment som gör att både extensions- och böjningsmoder kan exciteras och detekteras, framträder förlängningsmoden ofta som en prekursor med högre hastighet och lägre amplitud till böjningsmoden. Böjningsläget är det enklaste av de två och bär ofta det mesta av energin.

De högre ordningens lägen

När frekvensen höjs uppträder de högre ordningens våglägen förutom nollordningens lägen. Varje högre ordningsläge "föds" vid en resonansfrekvens hos plattan och existerar endast över den frekvensen. Till exempel, i en 3 ⁄ 4 tum (19 mm) tjock stålplåt med en frekvens på 200 kHz, är de första fyra Lamb-våglägena närvarande och vid 300 kHz, de första sex. De första få högre ordningens lägen kan tydligt observeras under gynnsamma experimentella förhållanden. Under mindre gynnsamma förhållanden överlappar de varandra och kan inte särskiljas.

De högre ordningens lammlägen kännetecknas av nodplan inom plattan, parallella med plattytorna. Var och en av dessa lägen existerar endast över en viss frekvens som kan kallas dess "begynnande frekvens". Det finns ingen övre frekvensgräns för något av lägena. De begynnande frekvenserna kan avbildas som resonansfrekvenserna för longitudinella eller skjuvvågor som utbreder sig vinkelrätt mot plattans plan, dvs.

$d={\frac {n\lambda }{2}}\quad \quad {\text{or}}\quad \quad f={\frac { nc}{2d}}$

där n är vilket positivt heltal som helst. Här c vara antingen den longitudinella våghastigheten eller skjuvvågshastigheten, och för varje resulterande uppsättning resonanser är motsvarande Lamb-vågmoder omväxlande symmetriska och antisymmetriska. Samspelet mellan dessa två uppsättningar resulterar i ett mönster av begynnande frekvenser som vid första anblicken verkar oregelbundna. Till exempel, i en 3/4 tum (19 mm) tjock stålplåt med longitudinella och skjuvhastigheter på 5890 m/s respektive 3260 m/s, de begynnande frekvenserna för de antisymmetriska lägena A 1 _och A ₂ är 86 kHz respektive 310 kHz, medan begynnande frekvenser för de symmetriska moderna S1, _S2 och S3 _{är 155 kHz ,} 172 kHz respektive 343 kHz.

Vid sin begynnande frekvens har var och en av dessa moder en oändlig fashastighet och en grupphastighet på noll. I högfrekvensgränsen konvergerar fas- och grupphastigheterna för alla dessa moder till skjuvvågshastigheten. På grund av dessa konvergenser är Rayleigh- och skjuvhastigheterna (som ligger mycket nära varandra) av stor betydelse i tjocka plattor. Enkelt uttryckt i termer av det material som har störst ingenjörsmässig betydelse, färdas det mesta av den högfrekventa vågenergin som utbreder sig långa sträckor i stålplåtar med 3000–3300 m/s.

Partikelrörelse i lammvågslägena är i allmänhet elliptisk, med komponenter både vinkelräta mot och parallella med plattans plan. Dessa komponenter är i kvadratur, dvs de har en fasskillnad på 90°. Komponenternas relativa storlek är en funktion av frekvensen. För vissa produkter med frekvenstjocklek passerar amplituden för en komponent genom noll så att rörelsen är helt vinkelrät eller parallell med plattans plan. För partiklar på plattans yta uppstår dessa förhållanden när lammvågens fashastighet är √ 2 c _t eller för symmetriska lägen endast c _l , respektive. Dessa riktningsöverväganden är viktiga när man överväger utstrålningen av akustisk energi från plattor till intilliggande vätskor.

Partikelrörelsen är också helt vinkelrät eller helt parallell med plattans plan, vid ett läges begynnande frekvens. Nära de begynnande frekvenserna för moder som motsvarar longitudinella vågresonanser hos plattan, kommer deras partikelrörelse att vara nästan helt vinkelrät mot plattans plan; och nära skjuvvågsresonanserna, parallella.

J. och H. Krautkrämer har påpekat att lammvågor kan tänkas som ett system av longitudinella och skjuvvågor som utbreder sig i lämpliga vinklar över och längs plattan. Dessa vågor reflekterar och mod-konverterar och kombinerar för att producera ett ihållande, koherent vågmönster. För att detta koherenta vågmönster ska bildas måste plåttjockleken vara precis rätt i förhållande till utbredningsvinklarna och våglängderna för de underliggande longitudinella vågorna och skjuvvågorna; detta krav leder till hastighetsspridningsförhållandena.

Lammvågor med cylindrisk symmetri; plattvågor från punktkällor

Medan Lambs analys antog en rak vågfront, har det visat sig att samma karakteristiska ekvationer gäller för cylindriska plattvågor (dvs vågor som fortplantar sig utåt från en linjekälla, linjen ligger vinkelrätt mot plattan). Skillnaden är att medan "bäraren" för den raka vågfronten är en sinusform, är "bäraren" för den axisymmetriska vågen en Bessel-funktion. Bessel-funktionen tar hand om singulariteten vid källan och konvergerar sedan mot sinusformigt beteende på stora avstånd.

Dessa cylindriska vågor är de egenfunktioner som plattans svar på punktstörningar kan bestå av. Således kan en plattas svar på en punktstörning uttryckas som en kombination av lammvågor, plus försvinnande termer i närfältet. Det övergripande resultatet kan löst visualiseras som ett mönster av cirkulära vågfronter, som krusningar från en sten som tappats i en damm men som förändras djupare i form när de går utåt. Lammvågsteorin relaterar endast till rörelse i (r,z) riktningen; tvärgående rörelse är ett annat ämne.

Guidade lammvågor

Denna fras påträffas ganska ofta i oförstörande tester. "Guided Lamb Waves" kan definieras som lammliknande vågor som styrs av de ändliga dimensionerna hos verkliga testobjekt. Att lägga till prefixet "guided" till frasen "Lamb wave" är alltså att inse att Lamms oändliga platta i verkligheten inte finns någonstans.

I verkligheten har vi att göra med ändliga plattor, eller plattor inlindade i cylindriska rör eller kärl, eller plattor skurna i tunna remsor, etc. Lammvågsteorin ger ofta en mycket bra redogörelse för mycket av vågbeteendet hos sådana strukturer. Det kommer inte att ge en perfekt redogörelse, och det är därför frasen "Guided Lamb Waves" är mer praktiskt relevant än "Lamb Waves". En fråga är hur hastigheterna och formerna för de lammliknande vågorna kommer att påverkas av delens verkliga geometri. Till exempel kommer hastigheten för en lammliknande våg i en tunn cylinder att bero något på cylinderns radie och på om vågen färdas längs axeln eller runt omkretsen. En annan fråga är vilka helt olika akustiska beteenden och våglägen som kan finnas i delens verkliga geometri. Till exempel har ett cylindriskt rör böjningssätt förknippade med kroppsrörelse av hela röret, helt annorlunda än det lammliknande böjningsläget för rörväggen.

Lammvågor i ultraljudstestning

Syftet med ultraljudstestning är vanligtvis att hitta och karakterisera individuella brister i det föremål som testas. Sådana brister detekteras när de reflekterar eller sprider den infallande vågen och den reflekterade eller spridda vågen når sökenheten med tillräcklig amplitud.

Traditionellt har ultraljudstestning utförts med vågor vars våglängd är mycket kortare än dimensionen på den del som inspekteras. I denna högfrekvensregim använder ultraljudsinspektören vågor som närmar sig de oändliga-medium longitudinella och skjuvvågslägena, sicksackande till och från tvärs över plattans tjocklek. Även om lammvågspionjärerna arbetade med oförstörande testapplikationer och uppmärksammade teorin, kom en utbredd användning inte till förrän på 1990-talet när datorprogram för att beräkna spridningskurvor och relatera dem till experimentellt observerbara signaler blev mycket mer allmänt tillgängliga. Dessa beräkningsverktyg, tillsammans med en mer utbredd förståelse av naturen hos lammvågor, gjorde det möjligt att utveckla tekniker för oförstörande testning med hjälp av våglängder som är jämförbara med eller större än plattans tjocklek. Vid dessa längre våglängder är dämpningen av vågen mindre så att brister kan detekteras på större avstånd.

En stor utmaning och skicklighet i användningen av lammvågor för ultraljudstestning är genereringen av specifika lägen vid specifika frekvenser som kommer att spridas väl och ge rena retur-"ekon". Detta kräver noggrann kontroll av exciteringen. Tekniker för detta inkluderar användningen av kamgivare, kilar, vågor från flytande media och elektromagnetiska akustiska givare ( EMAT ).

Lammvågor i akusto-ultraljudstestning

Akusto-ultraljudstestning skiljer sig från ultraljudstestning genom att det var tänkt som ett sätt att bedöma skador (och andra materiella egenskaper) fördelade över betydande områden, snarare än att karakterisera brister individuellt. Lammvågor är väl lämpade för detta koncept, eftersom de bestrålar hela plåttjockleken och fortplantar sig stora avstånd med konsekventa rörelsemönster.

Lammvågor i akustisk emissionstestning

Akustisk emission använder mycket lägre frekvenser än traditionell ultraljudstestning, och sensorn förväntas vanligtvis upptäcka aktiva brister på avstånd upp till flera meter. En stor del av de strukturer som vanligtvis testas med akustisk emission är tillverkade av stålplåt - tankar, tryckkärl, rör och så vidare. Lammvågsteorin är därför den främsta teorin för att förklara de signalformer och utbredningshastigheter som observeras när man utför akustisk emissionstestning. Betydande förbättringar i noggrannheten av AE-källans lokalisering (en viktig teknik för AE-testning) kan uppnås genom god förståelse och skickligt utnyttjande av Lamm-vågens kunskap.

Ultraljud och akustisk emissionstestning stod i kontrast

En godtycklig mekanisk excitation som appliceras på en platta kommer att generera ett flertal lammvågor som bär energi över en rad frekvenser. Så är fallet för den akustiska emissionsvågen. I akustisk emissionstestning är utmaningen att känna igen de multipla Lamb-vågkomponenterna i den mottagna vågformen och att tolka dem i termer av källrörelse. Detta står i kontrast till situationen vid ultraljudstestning, där den första utmaningen är att generera ett enda, välkontrollerat lammvågsläge vid en enda frekvens. Men även i ultraljudstestning sker modomvandling när den genererade Lamb-vågen interagerar med brister, så tolkningen av reflekterade signaler sammansatta från flera lägen blir ett sätt att karakterisera fel.

Se även

• Akustik
• Akustisk våg
• Våg ekvation
• Vågledare
• Vågledare (akustik)
• Vågledare (elektromagnetism)

• Rose, JL; "Ultrasonic Waves in Solid Media," Cambridge University Press, 1999.

externa länkar

• Lägen för ljudvågspridning vid NDT Resource Center
• Lammvåg i Nodestructive Testing Encyclopedia
• Lamb Wave Analysis of Acousto-Ultrasonic Signals in Plate av Liu Zhenqing: en artikel som inkluderar de fullständiga lammvågsekvationerna.