Kosnitas sats
I euklidisk geometri är Kosnitas sats en egenskap hos vissa cirklar associerade med en godtycklig triangel .
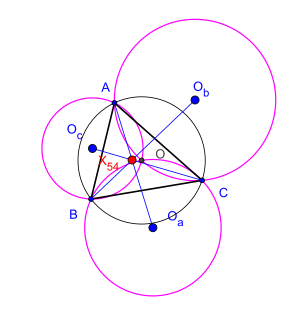
Låt vara en godtycklig triangel, dess omkrets och är omkretsen av tre trianglar , respektive . Satsen hävdar att de tre räta linjerna , och är samtidiga. Detta resultat fastställdes av den rumänske matematikern Cezar Coşniţă (1910-1962).
Deras överensstämmelsepunkt är känd som triangelns Kosnita-punkt (namngiven av Rigby 1997). Det är det isogonala konjugatet av niopunktscentrumet . Det är triangelcentrum i Clark Kimberlings lista . Denna sats är ett specialfall av Daos sats om sex cirkumcenter associerade med en cyklisk hexagon i.
- ^ Weisstein, Eric W. "Kosnita-satsen" . MathWorld .
- ^ Ion Pătraşcu (2010), En generalisering av Kosnitas teorem (på rumänska)
- ^ Darij Grinberg (2003), Om Kosnita pekar och reflektionstriangeln . Forum Geometricorum , volym 3, sid 105–111. ISSN 1534-1178
- ^ John Rigby (1997), Korta anteckningar om några bortglömda geometriska satser. Mathematics and Informatics Quarterly, volym 7, sidorna 156-158 (som citeras av Kimberling).
- ^ Clark Kimberling (2014), Encyclopedia of Triangle Centers Archived 2012-04-19 at the Wayback Machine , avsnitt X(54) = Kosnita Point . Åtkomst 2014-10-08
- ^ Nikolaos Dergiades (2014), Daos sats om sex omkretscentrum associerade med en cyklisk hexagon . Forum Geometricorum , volym 14, sid=243–246. ISSN 1534-1178 .
- ^ Telv Cohl (2014), ett rent syntetiskt bevis på Daos sats om sex cirkumcenter associerade med en cyklisk hexagon . Forum Geometricorum , volym 14, sid 261–264. ISSN 1534-1178 .
- ^ Ngo Quang Duong, International Journal of Computer Discovered Mathematics, Några problem kring Daos teorem om sex circumcenters associerade med en cyklisk hexagonkonfiguration, volym 1, sidor=25-39. ISSN 2367-7775
- ^ Clark Kimberling (2014), X(3649) = KS(INTOUCH TRIANGLE)
- ^ Nguyễn Minh Hà, ett annat rent syntetiskt bevis på Daos sats om Sixcircumcenters . Journal of Advanced Research on Classical and Modern Geometries, ISSN 2284-5569 , volym 6, sidorna 37–44. MR ....
- ^ Nguyễn Tiến Dũng, ett enkelt bevis på Daos sats om Sixcircumcenters . Journal of Advanced Research on Classical and Modern Geometries, ISSN 2284-5569 , volym 6, sidorna 58–61. MR ....
- ^ Förlängningen från en cirkel till en konisk med centrum: Den kreativa metoden för nya teorems, International Journal of Computer Discovered Mathematics, pp.21-32.
Kategori: