XOR-port

Den här artikeln handlar om XOR digital logic gate (t.ex. SN7486 eller CD4030B). För logisk XOR-operation, se Exklusiv eller . För annan användning, se XOR (disambiguation) .

Inmatning		Produktion
A	B	A XOR B
0	0	0
0	1	1
1	0	1
1	1	0

XOR-grind (ibland EOR , eller EXOR och uttalas som Exclusive OR ) är en digital logisk grind som ger en sann (1 eller HIGH) utgång när antalet sanna ingångar är udda. En XOR-grind implementerar en exklusiv eller ( $\nleftrightarrow$ ) från matematisk logik ; det vill säga en sann utsignal blir resultatet om en, och endast en, av ingångarna till grinden är sann. Om båda ingångarna är falska (0/LOW) eller båda är sanna, uppstår en falsk utdata. XOR representerar ojämlikhetsfunktionen, dvs utmatningen är sann om ingångarna inte är lika, annars är utmatningen falsk. Ett sätt att komma ihåg XOR är "måste ha det ena eller det andra men inte båda".

En XOR-grind kan fungera som en "programmerbar inverterare" i vilken en ingång bestämmer om den andra ingången ska inverteras eller helt enkelt skicka den vidare utan någon förändring. Därför fungerar den som en växelriktare (en NOT-grind) som kan aktiveras eller avaktiveras av en omkopplare.

XOR kan också ses som additionsmodulo 2. Som ett resultat används XOR-grindar för att implementera binär addition i datorer. En halvadderare består av en XOR-grind och en AND-grind . Grinden används också i subtraktorer och komparatorer .

De algebraiska uttrycken $A\cdot {\overline {B}}+{\overline {A}}\cdot B$ eller $(A+B)\cdot ({\overline {A}}+{\overline {B}})$ eller $A\oplus B$ representerar alla XOR-grinden med ingångarna A och B . XORs beteende sammanfattas i sanningstabellen som visas till höger.

Symboler

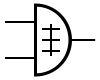
Det finns tre schematiska symboler för XOR-grindar: de traditionella ANSI- och DIN-symbolerna och IEC- symbolen. I vissa fall används DIN-symbolen med ⊕ istället för ≢. För mer information se Logic Gate-symboler .

ANSI XOR Schematisk symbol		IEC XOR Schematisk symbol		DIN XOR Schematisk symbol

De logiska symbolerna ⊕, Jpq . och ⊻ kan användas för att beteckna en XOR-operation i algebraiska uttryck

C-liknande språk använder fältsymbolen ^ för att beteckna bitvis XOR . (Observera att raden inte betecknar logisk konjunktion (AND) i dessa språk, trots likheten mellan symboler.)

Genomförande

XOR-grinden implementeras oftast med MOSFET- kretsar. Några av dessa implementeringar inkluderar:

CMOS

Den komplementära metall-oxid-halvledarimplementeringen ( CMOS ) av XOR-grinden.

CMOS XOR-grind

nMOS- och pMOS- transistorerna är arrangerade så att ingångsparen $A\cdot {\overline {B}}}$ displaystyle och ${\overline {A}}\cdot B$ aktiveras 2 pMOS-transistorerna längst upp till vänster respektive 2 pMOS-transistorerna uppe till höger, ansluter Vdd till utgången för en logisk hög. De återstående ingångsparen $A\cdot B$ och ${\overline {A}}\cdot {\overline {B}}$ aktiverar var och en av de två nMOS-vägarna i botten till Vss för en logisk låg.

Detta är en implementering med tolv transistorer eftersom ytterligare två växelriktare med två grindar vardera, som inte visas i diagrammet, behövs för att generera ${\overline {A}}$ och ${\overline {B} }$ .

Överföringsportar

XOR-grinden kan också implementeras genom användning av överföringsgrindar med passtransistorlogik .

Transmission gate implementering av XOR gate

Denna implementering använder två transmissionsgrindar och två växelriktare som inte visas i diagrammet för att generera ${\overline {A}}$ och ${\overline {B}}$ för totalt åtta transistorer, fyra mindre än i den tidigare designen. XOR-funktionen implementeras genom att skicka det inverterade värdet av A till utgången när B är högt och passera värdet på A när B är logiskt lågt. så när båda ingångarna är låga är transmissionsgrinden längst ner av och den längst upp är på och släpper igenom A som är låg så utgången är låg. När båda är höga är bara den nedersta aktiv och släpper igenom det inverterade värdet på A och eftersom A är hög blir uteffekten återigen låg. På liknande sätt om B förblir hög men A är låg skulle utmatningen vara ${\overline {A}}$ vilket är högt som förväntat och om B är lågt men A är högt går värdet av A igenom och utsignalen är hög fyller i sanningstabellen för XOR-porten.

Avvägningen med den tidigare implementeringen är att eftersom transmissionsgrindar inte är en idealisk switch, finns det ett resistans förknippat med dem, så beroende på signalstyrkan på ingången kan kaskadförsämring av utnivåerna försämras.

Optimerad pass-gate-logikkabel

Den tidigare implementeringen av transmissionsgrind kan optimeras ytterligare från åtta till sex transistorer genom att implementera funktionaliteten hos växelriktaren som genererar ${\overline {A}}$ och bottenpassporten med bara två transistorer arrangerade som en växelriktare men med källan för pMOS ansluten till $B$ istället för Vdd och källan för nMOS ansluten till ${\overline {B}}$ istället för GND.

Optimerad transmission Gate Logic kabeldragning av en XOR-grind

De två transistorerna längst till vänster som nämnts ovan, utför en optimerad villkorlig inversion av A när B är på en logisk hög nivå med användning av passtransistorlogik för att reducera transistorantalet och när B är på ett logiskt lågt, är deras utsignal i ett högimpedanstillstånd. De två i mitten är en transmissionsgrind som driver utsignalen till värdet av A när B är logiskt låg och de två transistorerna längst till höger bildar en inverterare som behövs för att generera ${\overline {B}}$ som används genom transmissionsgrinden och passtransistorns logikkrets.

Liksom med den tidigare implementeringen bör den direkta anslutningen av ingångarna till utgångarna genom pass-gate-transistorerna eller genom de två transistorerna längst till vänster tas med i beräkningen, speciellt när de kaskadkopplas.

Alternativ

XOR-grindkrets med tre blandade grindar

Om en specifik typ av grind inte är tillgänglig kan en krets som implementerar samma funktion konstrueras från andra tillgängliga grindar. En krets som implementerar en XOR-funktion kan trivialt konstrueras från en XNOR-grind följt av en NOT-grind . Om vi ​​betraktar uttrycket ${\displaystyle (A\cdot {\overline {B}})+({\overline {A}}\cdot B)} ,$ kan vi konstruera en XOR-grindkrets direkt med AND-, OR- och NOT-grindar . Detta tillvägagångssätt kräver dock fem grindar av tre olika slag.

Som ett alternativ, om olika grindar är tillgängliga kan vi använda boolesk algebra för att transformera ${\displaystyle (A\cdot { \overline {B}})+({\overline {A}}\cdot B)\equiv (A+B)\cdot ({\overline {A}}+{\overline {B}})} enligt$ ovan , och tillämpa de Morgans lag på den sista termen för att få $(A+B)\cdot {\overline {(A\cdot B)}}$ som kan vara implementeras med endast tre grindar som visas till höger. intuitivt är XOR ekvivalent med OR förutom när både A och B är höga. Så OCH för ELLER med sedan NAND som ger en låg endast när både A och B är höga är ekvivalent med XOR.

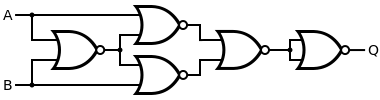
En XOR-grindkrets kan tillverkas av fyra NAND-grindar . Faktum är att både NAND- och NOR-grindar är så kallade "universella grindar" och vilken logisk funktion som helst kan konstrueras från antingen NAND-logik eller NOR-logik enbart. Om de fyra NAND-grindarna ersätts av NOR-grindar , resulterar detta i en XNOR-grind , som kan konverteras till en XOR-grind genom att invertera utgången eller en av ingångarna (t.ex. med en femte NOR-grind ).

Önskad grind	NAND-konstruktion	NOR konstruktion

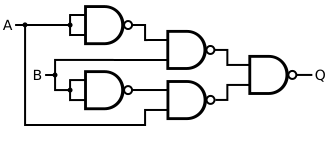
Ett alternativt arrangemang är fem NOR-grindar i en topologi som betonar konstruktionen av funktionen från ${\displaystyle (A+B)\cdot ({\overline {A}} +{\overline {B}})} ,$ noterar från de Morgans lag att en NOR-grind är en inverterad ingångs- OCH-grind . Ett annat alternativt arrangemang är fem NAND-grindar i en topologi som betonar konstruktionen av funktionen från $(A\cdot {\overline {B}})+({ \overline {A}}\cdot B)$ , och noterar från de Morgans lag att en NAND-grind är en ELLER-grind med inverterad ingång .

Önskad grind	NAND-konstruktion	NOR konstruktion

För NAND-konstruktionerna kräver det övre arrangemanget färre grindar. För NOR-konstruktionerna erbjuder det lägre arrangemanget fördelen av en kortare utbredningsfördröjning (tidsfördröjningen mellan en ingångsändring och utgångsändringen).

Standard chippaket

Philips 4070 quad dual input XOR-chip på kretskort

XOR-chips är lättillgängliga. De vanligaste standardchipkoderna är:

• 4070: CMOS quad dubbla ingångar XOR-grindar.
• 4030: CMOS quad dubbla ingångar XOR-grindar.
• 7486: TTL quad dubbla ingångar XOR-grindar.

Fler än två ingångar

Bokstavlig tolkning av namnet "exklusivt eller", eller observation av den rektangulära IEC-symbolen, väcker frågan om korrekt beteende med ytterligare ingångar. Om en logisk grind skulle acceptera tre eller fler ingångar och producera en sann utsignal om exakt en av dessa ingångar var sann, så skulle det i själva verket vara en en-varm- detektor (och detta är faktiskt fallet för endast två ingångar). Det är dock sällan implementerat på detta sätt i praktiken.

Det är vanligast att betrakta efterföljande ingångar som applicerade genom en kaskad av binära exklusiva-eller-operationer: de första två signalerna matas in i en XOR-grind, sedan matas utgången från den grinden till en andra XOR-grind tillsammans med den tredje signalen , och så vidare för eventuella återstående signaler. Resultatet är en krets som matar ut en 1 när antalet 1:or vid dess ingångar är udda, och en 0 när antalet inkommande 1:or är jämnt. Detta gör den praktiskt användbar som en paritetsgenerator eller en modulo-2- adderare .

Till exempel annonseras mikrochippet 74LVC1G386 som en logisk grind med tre ingångar och implementerar en paritetsgenerator.

Ansökningar

Exempel kretsschema för halv adderare

Exempel på komplett adderare kretsschema

XOR-grindar och AND-grindar är de två mest använda strukturerna i VLSI- applikationer.

Använder dessutom

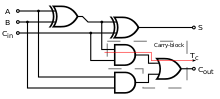
XOR-logikgrinden kan användas som en en-bits adderare som adderar vilka två bitar som helst för att mata ut en bit. Till exempel, om vi lägger till 1 plus 1 i binär , förväntar vi oss ett tvåbitars svar, 10 (dvs. 2 i decimal). Eftersom den avslutande summabiten i denna utgång uppnås med XOR, beräknas den föregående överföringsbiten med en OCH-grind . Detta är huvudprincipen i Half Adders . En något större Full Adder- krets kan kedjas ihop för att lägga till längre binära tal.

I vissa situationer kan ingångarna till en ELLER-grind (till exempel i en fulladderare) eller till en XOR-grind aldrig vara båda 1:orna. Eftersom detta är den enda kombinationen för vilken ELLER- och XOR-grindutgångarna skiljer sig åt, kan en ELLER-grind ersättas med en XOR-grind (eller vice versa) utan att den resulterande logiken ändras. Detta är praktiskt om kretsen implementeras med enkla integrerade kretschips som endast innehåller en grindtyp per chip.

Pseudo-slumptalsgenerator

Pseudo-slumptalsgeneratorer (PRN) , speciellt linjär-feedback-skiftregister (LFSR), definieras i termer av exklusiv-eller-operationen. Följaktligen kan en lämplig uppsättning av XOR-grindar modellera ett linjärt återkopplingsskiftregister för att generera slumptal.

Korrelation och sekvensdetektering

00 XOR-grindar producerar en när båda ingångarna matchar. När man söker efter ett specifikt bitmönster eller PRN-sekvens i en mycket lång datasekvens, kan en serie XOR-grindar användas för att jämföra en sträng bitar från datasekvensen mot målsekvensen parallellt. Antalet utgångar kan sedan räknas för att bestämma hur väl datasekvensen matchar målsekvensen. Korrelatorer används i många kommunikationsenheter såsom CDMA- mottagare och avkodare för felkorrigering och kanalkoder. I en CDMA-mottagare används korrelatorer för att extrahera polariteten hos en specifik PRN-sekvens ur en kombinerad samling av PRN-sekvenser.

En korrelator som letar efter 11010 i datasekvensen 1110100101 skulle jämföra de inkommande databitarna mot målsekvensen vid varje möjlig offset samtidigt som den räknar antalet matchningar (nollor):

1110100101 (data) 11010 (mål) 00111 (XOR) 2 nollbitar 1110100101 11010 00000 5 nollbitar 1110100101 11010 011010 1101010101010101010101010101 2 nollbitar 1110100101 11010 01000 4 nollbitar 1110100101 11010 11111 0 nollbitar Matchar efter offset: . : : : : : : : ----------- 0 1 2 3 4 5

I det här exemplet inträffar den bästa matchningen när målsekvensen är förskjuten med 1 bit och alla fem bitarna matchar. När den förskjuts med 5 bitar, matchar sekvensen exakt sin invers. Genom att titta på skillnaden mellan antalet ettor och nollor som kommer ut från banken av XOR-grindar är det lätt att se var sekvensen inträffar och om den är inverterad eller inte. Längre sekvenser är lättare att upptäcka än korta sekvenser.

Fasdetektorer

XOR-grindar kan användas i de enklaste fasdetektorerna .

Analytisk representation

$f(a,b)=a+b-2ab$ är en analytisk representation av XOR-grind:

• $f(0,0)=0+0-2\cdot 0\cdot 0=0$
• $f(0,1)=0+1-2\cdot 0\cdot 1=1$
• $f(1,0)=1+0-2\cdot 1\cdot 0=1$
• $f(1,1)=1+1-2\cdot 1\cdot 1=0$

$f(a,b)=|ab|$ är en alternativ analytisk representation.

Se även

• Exklusivt eller
• OCH grind
• ELLER grind
• Inverter (INTE gate)
• NAND-grind
• NOR-port
• XNOR-port
• IMPLERA grind
• Boolesk algebra
• Logisk grind