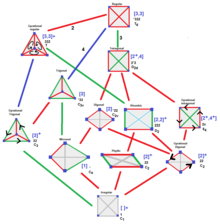
Konfiguration (polytop)

Inom geometri kallade HSM Coxeter en vanlig polytop för en speciell typ av konfiguration .

Andra konfigurationer inom geometri är något annat. Dessa polytopkonfigurationer kan mer exakt kallas incidensmatriser , där liknande element samlas ihop i rader och kolumner. Vanliga polytoper kommer att ha en rad och kolumn per k -face- element, medan andra polytoper kommer att ha en rad och kolumn för varje k-face-typ efter sina symmetriklasser. En polytop utan symmetri kommer att ha en rad och kolumn för varje element, och matrisen kommer att fyllas med 0 om elementen inte är anslutna, och 1 om de är anslutna. Element av samma k kommer inte att anslutas och kommer att ha en "*" tabellpost.

Varje polytop och abstrakt polytop har ett Hasse-diagram som uttrycker dessa kopplingar, som systematiskt kan beskrivas med en incidensmatris .

Konfigurationsmatris för vanliga polytoper

_för en vanlig polytop representeras av en matris där det diagonala elementet, Ni , är antalet i - ytor i polytopen. De diagonala elementen kallas också för en polytops f-vektor . Det icke-diagonala ( i ≠ j ) elementet N _ij är antalet j -ytor som faller in med varje i -face element, så att Ni _{N ij} = N _j N _ji .

Principen sträcker sig generellt till n dimensioner, där 0 ≤ j < n .

${\begin{bmatrix}{\begin{matrix}N_{0}&N_{0,1}&N_{0,2}&\cdots &N_{0,n-1}\ \N_{1,0}&N_{1}&N_{1,2}&\cdots &N_{1,n-1}\\\vdots &\vdots &\vdots &&\vdots \\N_{n-1,0 }&N_{n-1,1}&N_{n-1,2}&\cdots &N_{n-1}\end{matris}}\end{bmatrix}}$

Polygoner

En vanlig polygon , Schläfli-symbol { q }, kommer att ha en 2x2-matris, med den första raden för hörn och andra raden för kanter. Ordningen g är 2 q .  

${\begin{bmatrix}{\begin{matrix}N_{0}&N_{01} \\N_{10}&N_{1}\end{matrix}}\end{bmatrix}}={\begin{bmatrix}{\begin{matrix}g/2&2\\2&g/2\end{matrix}}\ end{bmatrix}}={\begin{bmatrix}{\begin{matrix}q&2\\2&q\end{matrix}}\end{bmatrix}}$

En allmän n-gon kommer att ha en 2n x 2n-matris, med de första n raderna och kolumnernas hörn, och de sista n raderna och kolumnerna som kanter.

Triangel exempel

Ytterligare information: Triangel § By_lengths_of_sides

Det finns tre symmetriklassificeringar av en triangel : liksidig, likbent och skalen. De har alla samma incidensmatris , men symmetri gör att hörn och kanter kan samlas ihop och räknas. Dessa trianglar har hörn märkta A,B,C och kanter a,b,c, medan hörn och kanter som kan mappas på varandra genom en symmetrioperation är märkta identiskt.

Trianglar

Liksidig {3}	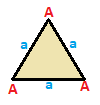Likbent { }∨( )	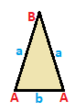Skala ( )∨( )∨( )
(v:3; e:3)	(v:2+1; e:2+1)	(v:1+1+1; e:1+1+1)
| A | a --+---+--- A | 3 | 2 --+---+--- a | 2 | 3	| AB | ab --+-----+----- A | 2 * | 1 1 B | * 1 | 2 0 --+-----+----- a | 1 1 | 2 * b | 2 0 | * 1	| ABC | abc --+-------+------- A | 1 * * | 0 1 1 B | * 1 * | 1 0 1 C | * * 1 | 1 1 0 --+-------+------- a | 0 1 1 | 1 * * b | 1 0 1 | * 1 * c | 1 1 0 | * * 1

Fyrhörningar

Ytterligare information: Square § Symmetri

Fyrhörningar genom symmetri

Fyrhörningar kan klassificeras efter symmetri, var och en med sin egen matris. Fyrhörningar finns med dubbla par som kommer att ha samma matris, roterad 180 grader, med hörn och kanter omvända. Kvadrater och parallellogram och allmänna fyrhörningar är självduala klassmässigt så deras matriser är oförändrade när de roteras 180 grader.

Fyrhörningar

Fyrkant {4}	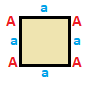Rektangel { }×{ }	Rhombus { }+{ }	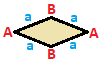Parallellogram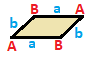
(v:4; e:4)	(v:4; e:2+2)	(v:2+2; e:4)	(v:2+2; e:2+2)
| A | a --+---+--- A | 4 | 2 --+---+--- a | 2 | 4	| A | ab --+---+----- A | 4 | 1 1 --+---+----- a | 2 | 2 * b | 2 | * 2	| AB | a --+-----+--- A | 2 * | 2 B | * 2 | 2 --+-----+--- a | 1 1 | 4	| AB | ab --+-----+----- A | 2 * | 1 1 B | * 2 | 1 1 --+-----+----- a | 1 1 | 2 * b | 1 1 | * 2
Likbent trapets { }||{ }	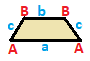Drake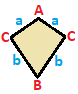	Allmän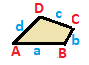
(v:2+2; e:1+1+2)	(v:1+1+2; e:2+2)	(v:1+1+1+1; e:1+1+1+1)
| AB | abc --+-----+------- A | 2 * | 1 0 1 B | * 2 | 0 1 1 --+-----+------ a | 2 0 | 1 * * b | 0 2 | * 1 * c | 1 1 | * * 2	| ABC | ab --+-------+---- A | 1 * * | 2 0 B | * 1 * | 0 2 C | * * 2 | 1 1 --+-------+---- a | 1 0 1 | 2 * b | 0 1 1 | * 2	| ABCD | abcd --+---------+-------- A | 1 * * * | 1 0 0 1 B | * 1 * * | 1 1 0 0 C | * * 1 * | 0 1 1 0 D | * * * 1 | 0 0 1 1 --+---------+-------- a | 1 1 0 0 | 1 * * * b | 0 1 1 0 | * 1 * * c | 0 0 1 1 | * * 1 * d | 1 0 0 1 | * * * 1

Komplexa polygoner

Idén är också tillämplig för vanliga komplexa polygoner , _p { q } _r , konstruerade i $\mathbb {C} ^{2}$ :

${\begin{bmatrix}{\begin{matrix}N_{0}&N_{01}\\N_{10}&N_ {1}\end{matrix}}\end{bmatrix}}={\begin{bmatrix}{\begin{matrix}g/r&r\\p&g/p\end{matrix}}\end{bmatrix}}$

Den komplexa reflektionsgruppen är _p [ q ] _r , ordningen $g=8/q\cdot (1/p+ 2/q+1/r-1)^{-2}$ .

Polyedra

Se även: Platonsk solid § Som en konfiguration

Idén kan appliceras i tre dimensioner genom att överväga incidensen av punkter, linjer och plan, eller j -mellanrum (0 ≤ j < 3) , där varje j -rum är infallande med N _jk k -rum ( j ≠ k ) . Genom att skriva N _j för antalet närvarande j -mellanslag kan en given konfiguration representeras av matrisen

 ${\displaystyle {\begin{bmatrix}{\ börja{matris}N_{0}&N_{01}&N_{02}\\N_{10}&N_{1}&N_{12}\\N_{20}&N_{21}&N_{2}\slut{matris}} \end{bmatrix}}={\begin{bmatrix}{\begin{matrix}g/2q&q&q\\2&g/4&2\\p&p&g/2p\end{matrix}}\end{bmatrix}}} för Schläfli-symbol {$ p ,q}, med gruppordning g = 4 pq /(4 − ( p − 2)( q − 2)).

Tetraeder

Ytterligare information: Tetrahedron § Isometries_of_irregular_tetrahedra

Symmetrier av tetraedrar

Tetraedrar har matriser som också kan grupperas efter sin symmetri, med en allmän tetraeder som har 14 rader och kolumner för de 4 hörnen, 6 kanterna och 4 ytorna. Tetraedrar är självdubbla, och roterande matices 180 grader (byte av hörn och ytor) kommer att lämna det oförändrat.

Tetraedrar

Vanlig (v:4; e:6; f:4)	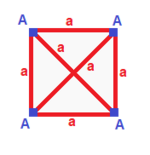tetragonal disfenoid (v:4; e:2+4; f:4)	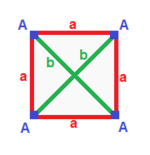Rombisk disfenoid (v:4; e:2+2+2; f:4)	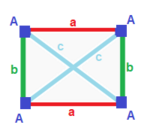Digonal disfenoid (v:2+2; e:4+1+1; f:2+2)	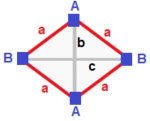Fyllisk disfenoid (v:2+2; e:2+2+1+1; f:2+2)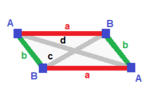
A| 4 | 3 | 3 ---+---+---+-- a| 2 | 6 | 2 ---+---+---+-- aaa| 3 | 3 | 4	A| 4 | 2 1 | 3 ---+---+-----+-- a| 2 | 4 * | 2 b| 2 | * 2 | 2 ---+---+-----+-- aab| 3 | 2 1 | 4	A| 4 | 1 1 1 | 3 ----+---+-------+-- a| 2 | 2 * * | 2 b| 2 | * 2 * | 2 c| 2 | * * 2 | 2 ----+---+-------+-- abc| 3 | 1 1 1 | 4	A| 2 * | 2 1 0 | 2 1 B| * 2 | 2 0 1 | 1 2 ---+-----+-------+---- a| 1 1 | 4 * * | 1 1 b| 2 0 | * 1 * | 2 0 c| 0 2 | * * 1 | 0 2 ---+-----+-------+---- aab| 2 1 | 2 1 0 | 2 * aac| 1 2 | 2 0 1 | * 2	A| 2 * | 1 0 1 1 | 1 2 B| * 2 | 1 1 1 0 | 2 1 ---+-----+--------+---- a| 1 1 | 2 * * * | 1 1 b| 1 1 | * 2 * * | 1 1 c| 0 2 | * * 1 * | 2 0 d| 2 0 | * * * 1 | 0 2 ---+-----+--------+---- abc| 1 2 | 1 1 1 0 | 2 * bcd| 2 1 | 1 1 0 1 | * 2
Triangulär pyramid (v:3+1; e:3+3; f:3+1)	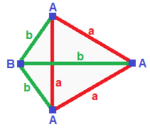Speglad sfäroid (v:2+1+1; e:2+2+1+1; f:2+1+1)	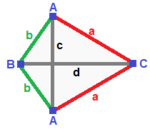	Ingen symmetri (v:1+1+1+1; e:1+1+1+1+1+1; f:1+1+1+1)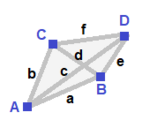
A| 3 * | 2 1 | 2 1 B| * 1 | 0 3 | 3 0 ---+-----+-----+---- a| 2 0 | 3 * | 1 1 b| 1 1 | * 3 | 2 0 ---+-----+-----+---- abb| 2 1 | 1 2 | 3 * aaa| 3 0 | 3 0 | * 1	A| 2 * * | 1 1 0 1 | 1 1 1 B| * 1 * | 2 0 1 0 | 0 2 1 C| * * 1 | 0 2 1 0 | 1 2 0 ---+-------+--------+------ a| 1 0 1 | 2 * * * | 0 1 1 b| 0 1 1 | * 2 * * | 1 1 0 c| 1 1 0 | * * 1 * | 0 2 0 d| 0 0 2 | * * * 1 | 1 0 1 ---+------+---------+------ ABC| 1 1 1 | 1 1 1 0 | 2 * * ACC| 1 0 2 | 2 0 0 1 | * 1 * BCC| 0 1 2 | 0 2 0 1 | * * 1		A | 1 0 0 0 | 1 1 1 0 0 0 | 1 1 1 0 B | 0 1 0 0 | 1 0 0 1 1 0 | 1 1 0 1 C | 0 0 1 0 | 0 1 0 1 0 1 | 1 0 1 1 D | 0 0 0 1 | 0 0 1 0 1 1 | 0 1 1 1 ----+---------+-------------------+-------- a | 1 1 0 0 | 1 0 0 0 0 0 | 1 1 0 0 b | 1 0 1 0 | 0 1 0 0 0 0 | 1 0 1 0 c | 1 0 0 1 | 0 0 1 0 0 0 | 0 1 1 0 d | 0 1 1 0 | 0 0 0 1 0 0 | 1 0 0 1 e | 0 1 0 1 | 0 0 0 0 1 0 | 0 1 0 1 f | 0 0 1 1 | 0 0 0 0 0 1 | 0 0 1 1 ----+---------+-------------+-------- ABC | 1 1 1 0 | 1 1 0 1 0 0 | 1 0 0 0 ABD | 1 1 0 1 | 1 0 1 0 1 0 | 0 1 0 0 ACD | 1 0 1 1 | 0 1 1 0 0 1 | 0 0 1 0 BCD | 0 1 1 1 | 0 0 0 1 1 1 | 0 0 0 1

Anteckningar

• Coxeter, HSM (1948), Regular Polytopes Methuen och Co. ,
•   Coxeter, HSM (1991), Regular Complex Polytopes , Cambridge University Press, ISBN 0-521-39490-2
•   Coxeter, HSM (1999), "Självdubbla konfigurationer och vanliga grafer", The Beauty of Geometry , Dover, ISBN 0-486-40919-8