Kobon triangelproblem

Kobon-trianglar genererade med 3, 4 och 5 raka linjesegment.

Olöst problem i matematik :

Hur många icke-överlappande trianglar kan bildas i ett arrangemang av $k$ linjer?

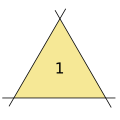
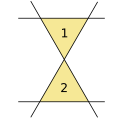
Kobon -triangelproblemet är ett olöst problem inom kombinatorisk geometri som först angavs av Kobon Fujimura (1903-1983). Problemet frågar efter det största antalet N ( k ) av icke-överlappande trianglar vars sidor ligger på ett arrangemang av k linjer . Variationer av problemet tar hänsyn till det projektiva planet snarare än det euklidiska planet, och kräver att trianglarna inte korsas av några andra linjer i arrangemanget.

Kända övre gränser

Saburo Tamura bevisade att antalet icke-överlappande trianglar som kan realiseras med $k$ linjer är som mest $\lfloor k(k-2)/3\rfloor$ . G. Clément och J. Bader bevisade starkare att denna gräns inte kan uppnås när $k$ är kongruent med 0 eller 2 (mod 6). Det maximala antalet trianglar är därför högst en mindre i dessa fall. Samma gränser kan på motsvarande sätt anges, utan användning av golvfunktionen , som :

{\begin{cases}{\frac {1}{3}}k(k-2)&{\text{när }}k\equiv 3,5{\pmod {6}};\\{ \frac {1}{3}}(k+1)(k-3)&{\text{när }}k\equiv 0,2{\pmod {6}};\\{\frac {1}{ 3}}(k^{2}-2k-2)&{\text{när }}k\equiv 1,4{\pmod {6}}.\end{cases}}

Lösningar som ger detta antal trianglar är kända när $k$ är 3, 4, 5, 6, 7, 8, 9, 13, 15 eller 17. För k = 10, 11 och 12 når de bästa kända lösningarna ett antal trianglar en mindre än den övre gränsen.

Kända konstruktioner

₀ Givet en perfekt lösning med k > 3 linjer, ^{[ förtydligande behövs ]} kan andra Kobon-triangellösningsnummer hittas för alla k _i -värden där

k_{n+1}=2\cdot k_{n}-1,

₀ genom att använda proceduren av D. Forge och JL Ramirez Alfonsin. Till exempel leder lösningen för k = 5 till det maximala antalet icke-överlappande trianglar för k = 5, 9, 17, 33, 65, .... ^{[ misslyckad verifiering ]}

k	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	OEIS
Tamuras övre gräns på N ( k )	1	2	5	8	11	16	21	26	33	40	47	56	65	74	85	96	107	120	133	A032765
Clément och Baders övre gräns	1	2	5	7	11	15	21	26	33	39	47	55	65	74	85	95	107	119	133	-
mest kända lösningen	1	2	5	7	11	15	21	25	32	38	47	53	65	72	85	93	104	115	130	A006066