Kelvin–Helmholtz instabilitet

Ej att förväxla med Kelvin–Helmholtz-mekanismen .

Numerisk simulering av en tidsmässig Kelvin–Helmholtz-instabilitet

Kelvin –Helmholtz-instabiliteten (efter Lord Kelvin och Hermann von Helmholtz ) är en vätskeinstabilitet som uppstår när det finns hastighetsskjuvning i en enda kontinuerlig vätska eller en hastighetsskillnad över gränsytan mellan två vätskor . Kelvin-Helmholtz-instabiliteter är synliga i atmosfärerna hos planeter och månar, såsom i molnformationer på jorden eller den röda fläcken på Jupiter , och atmosfärerna hos solen och andra stjärnor .

Rumsligt utvecklande 2D Kelvin-Helmholtz-instabilitet vid lågt Reynolds-tal . Små störningar, påtvingade vid inloppet på tangentiell hastighet, utvecklas i beräkningsboxen. Högt Reynolds tal skulle markeras med en ökning av småskaliga rörelser.

Teoriöversikt och matematiska begrepp

En KH-instabilitet som görs synlig av moln, känd som fluctus , över Mount Duval i Australien

En KH-instabilitet på planeten Saturnus, bildad i samverkan mellan två band av planetens atmosfär

Kelvin-Helmholtz böljar 500 meter djupt i Atlanten

Animation av KH-instabiliteten, med hjälp av ett andra ordningens 2D-finit volymschema

Vätskedynamik förutsäger början av instabilitet och övergång till turbulent flöde inom vätskor med olika densitet som rör sig med olika hastigheter. Om ytspänning ignoreras, ger två vätskor i parallell rörelse med olika hastigheter och densiteter ett gränssnitt som är instabilt mot störningar med korta våglängder för alla hastigheter. Ytspänningen kan emellertid stabilisera den korta våglängdsinstabiliteten upp till en tröskelhastighet.

Om densiteten och hastigheten varierar kontinuerligt i rymden (med de lättare skikten överst, så att vätskan är RT-stabil ), beskrivs dynamiken i Kelvin-Helmholtz-instabiliteten av Taylor-Goldstein-ekvationen :

$$(Uc)^{2 }\left({d^{2}{\tilde {\phi }} \over dz^{2}}-k^{2}{\tilde {\phi}}\right)+\left[N^{ 2}-(Uc){d^{2}U \over dz^{2}}\right]{\tilde {\phi }}=0,$$

där ${\textstyle N={\sqrt {g/L_{\rho }}}}$ anger Brunt–Väisälä-frekvensen , U är den horisontella parallella hastigheten, k är vågtalet, c är egenvärdet parametern för problemet, ${\tilde {\phi }}$ är komplex amplitud för streamfunktionen . Dess början ges av Richardson-talet $\mathrm {Ri}$ . Vanligtvis är lagret instabilt för $\mathrm {Ri} <0,25$ . Dessa effekter är vanliga i molnlager. Studiet av denna instabilitet är tillämpbart inom plasmafysik, till exempel i tröghetsinneslutningsfusion och plasma - berylliumgränssnittet . I situationer där det finns ett tillstånd av statisk stabilitet, uppenbart av tyngre vätskor som finns nedanför än den lägre vätskan, kan Rayleigh-Taylor-instabiliteten ignoreras eftersom Kelvin-Helmholtz-instabiliteten är tillräcklig givet förhållandena.

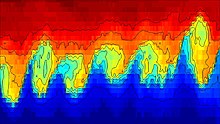
Numeriskt simuleras Kelvin–Helmholtz-instabiliteten i ett temporalt eller rumsligt tillvägagångssätt. I det tidsmässiga tillvägagångssättet betraktas flödet i en periodisk (cyklisk) ruta som "rör sig" med medelhastighet (absolut instabilitet). I det rumsliga tillvägagångssättet efterliknar simuleringar ett labbexperiment med naturliga inlopps- och utloppsförhållanden (konvektiv instabilitet).

Se även

• Rayleigh-Taylor instabilitet
• Richtmyer–Meshkov instabilitet
• Svampmoln
• Plateau–Rayleigh instabilitet
• Kármán virvelgatan
• Taylor–Couette-flöde
• Vätskemekanik
• Vätskedynamik
• Reynolds nummer
• Turbulens

Anteckningar

• Lord Kelvin (William Thomson) (1871). "Hydrokinetiska lösningar och observationer". Filosofisk tidskrift . 42 : 362-377.
• Hermann von Helmholtz (1868). "Über discontinuierliche Flüssigkeits-Bewegungen [Om vätskors diskontinuerliga rörelser]". Monatsberichte der Königlichen Preussische Akademie der Wissenschaften zu Berlin . 23 : 215-228.
• Artikel som beskriver upptäckten av KH-vågor i djuphavet: Broad, William J. (19 april 2010). "I djupt hav, vågor med en bekant krull" . New York Times . Hämtad 23 april 2010 .

externa länkar

• Hwang, K.-J.; Goldstein; Kuznetsova; Wang; Viñas; Sibeck (2012). "Den första observationen på plats av Kelvin-Helmholtz-vågor vid magnetopaus på hög latitud under starkt gryning mot interplanetära magnetfältsförhållanden". J. Geophys. Res . 117 (A08233): ej tillgänglig. Bibcode : 2012JGRA..117.8233H . doi : 10.1029/2011JA017256 . hdl : 2060/20140009615 .
• Jätte tsunamiformade moln rullar över Alabamas himmel - Natalie Wolchover, Livescience via Yahoo.com
• Tsunamimoln träffar Floridas kustlinje
• Vortexbildning i fri jet - YouTube-video som visar Kelvin Helmholtz-vågor på kanten av en fri jet visualiserad i ett vetenskapligt experiment.
• Vågmoln över Christchurch City
• Kelvin-Helmholtz moln, i Barmouth, Gwynedd, den 18 februari 2017