Johnson graf

Johnson-grafen
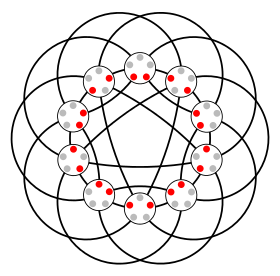Johnson-grafen
	Johnson-grafen J (5,2)
Döpt efter	Selmer M. Johnson
Vertices
Kanter
Diameter
Egenskaper	; ; ; -regular Vertex-transitiv Avstånd-transitiv Hamilton-ansluten
Notation
	Tabell över grafer och parametrar

Johnson-grafer är en speciell klass av oriktade grafer definierade från system av uppsättningar. Höjdpunkterna i Johnson-grafen $J(n,k)$ är $k$ -elementdelmängder av en $n$ -elementuppsättning; två hörn är intilliggande när skärningspunkten mellan de två hörnen (delmängder) innehåller $(k-1)$ -element. Både Johnson-graferna och det närbesläktade Johnson-schemat är uppkallade efter Selmer M. Johnson .

Speciella fall

$J(n,1)$ är hela grafen $K n$ .
$J(4,2)$ är den oktaedriska grafen .
$J(5,2)$ är komplementgrafen till Petersen-grafen , därav linjegrafen för $K 5$ . $K(n,2).$ generellt, för alla ${\displaystyle n} är$ Johnson-grafen $J(n,2)$ komplementet till Kneser-grafen

Grafteoretiska egenskaper

$J(n,k)$ är isomorf till $J(n,nk).$

För alla $0\leq j\leq \operatörsnamn {diam} (J(n,k))$ , vilket par av hörn som helst på avstånd $j$ delar $kj$ element gemensamt.

$J(n,k)$ är Hamilton-kopplad , vilket betyder att varje par av hörn bildar ändpunkterna för en Hamiltonsk bana i grafen. Detta betyder i synnerhet att den har en Hamiltonsk cykel.

Det är också känt att Johnson-grafen $J(n,k)~$ är $~k(nk)$ -vertex-kopplad.

$J(n,k)$ bildar grafen över hörn och kanter på en ( n − 1)-dimensionell polytop , kallad hypersimplex .

klicktalet för $J(n,k)$ ges av ett uttryck i termer av dess minsta och största egenvärden : ${\displaystyle \omega (J(n,k))=1-{\tfrac {\lambda _{\max }}{\lambda _{\min }}}.} Det$

kromatiska talet för $J(n,k)$ är som mest $n,\chi (J(n,k))\leq n.$

Automorfism grupp

Det finns en distanstransitiv undergrupp av $\operatorname {Aut} (J(n,k))$ isomorf till $\operatorname {Sym} (n)$ . Faktum är att ${\displaystyle \operatorname {Aut} (J(n,k))\cong \operatorname {Sym} (n)} ,$ om inte $n=2k\geq 4$ ; annars, $\operatorname {Aut} (J(n,k))\cong \operatorname {Sym} (n)\ gånger C_ {2}$ .

Intersection array

Som en konsekvens av att vara avståndstransitiv är $J(n,k)$ också avståndsreguljär . Låter ${\displaystyle d} beteckna dess diameter,$ ges skärningsmatrisen för ${\displaystyle J(n,k)} av$

\left\{b_{0},\ldots ,b_{d-1},c_{1},\ldots c_{d} \höger\}

var:

{\begin{aligned}b_{j}&=(kj)(nkj)&&0 \leq j<d\\c_{j}&=j^{2}&&0<j\leq d\end{aligned}}

Det visar sig att om inte $J(n,k)$ är $J(8,2)$ , delas dess skärningsmatris inte med något annat distinkt avstånd -vanlig graf; skärningsmatrisen för $J(8,2)$ delas med tre andra avstånds-reguljära grafer som inte är Johnson-grafer.

Egenvärden och egenvektorer

Det karakteristiska polynomet för $J(n,k)$ ges av

\phi (x):=\prod _{j=0}^{\operatörsnamn {diam} (J(n,k))}\left(x-A_{n,k}(j)\right )^{{\binom {n}{j}}-{\binom {n}{j-1}}}.

där

A_{n,k}(j)=(kj)(nkj)-j.

Egenvektorerna för $J(n,k)$ har en explicit beskrivning.

Johnsons schema

Johnson-grafen $J(n,k)$ är nära besläktad med Johnson-schemat , ett associationsschema där varje par av $k$ -elementuppsättningar är associerade med ett tal, hälften så stort som symmetrisk skillnad mellan de två uppsättningarna. Johnson-grafen har en kant för varje par av uppsättningar på avstånd ett i associationsschemat, och avstånden i associationsschemat är exakt de kortaste vägavstånden i Johnson-grafen.

Johnson-schemat är också relaterat till en annan familj av distanstransitiva grafer, de udda graferna , vars hörn är $k$ -elementdelmängder av ett $(2k+1)$ -element uppsättning och vars kanter motsvarar osammanhängande par av delmängder.

Öppna problem

Vertexexpansionsegenskaperna hos Johnson-grafer, liksom strukturen för motsvarande extrema uppsättningar av hörn av en given storlek, är inte helt klarlagda. Emellertid erhölls nyligen en asymptotiskt snäv nedre gräns för expansion av stora uppsättningar av hörn.

I allmänhet är det ett öppet problem att bestämma det kromatiska numret för en Johnson-graf.

Se även

Grassmann graf

externa länkar