Hypersimplex

Standard hypersimplices i $\mathbb {R} ^{3}$
$\Delta _{3,1}$ Hyperplan: $x+y+z=1$	$\Delta _{3,2}$ Hyperplan: $x+y+z=2$

I polyedrisk kombinatorik är hypersimplexet $\Delta _{d,k}$ en konvex polytop som generaliserar simplexet . Den bestäms av två heltal $d$ och $k$ , och definieras som det konvexa skrovet för de $d$ -dimensionella vektorerna vars koefficienter består av $k$ ettor och $dk$ nollor. På motsvarande sätt $\Delta _{d,k}$ erhållas genom att skära upp den $d$ -dimensionella enheten hyperkuben $[0,1]^{d }$ med ekvationens hyperplan $x_{1}+\cdots +x_{d}=k$ och av denna anledning är det a ${\ displaystyle (d-1)}$ -dimensionell polytop när $0<k<d$ .

Egenskaper

Antalet hörn för $\Delta _{d,k}$ är ${\tbinom {d}{k}}$ . Grafen som bildas av hörnen och kanterna på hypersimplexet $\Delta _{d,k}$ är Johnson-grafen $J(d,k)$ .

Alternativa konstruktioner

En alternativ konstruktion (för ${\displaystyle k\leq {d/2}} )$ är att ta det konvexa skrovet av alla $(d-1)$ -dimensionella $(0,1)$ -vektorer som har antingen $k-1$ eller $k$ koordinater som inte är noll. Detta har fördelen av att arbeta i ett utrymme som har samma dimension som den resulterande polytopen, men nackdelen att polytopen den producerar är mindre symmetrisk (även om kombinatoriskt motsvarar resultatet av den andra konstruktionen).

Hypersimplexen $\Delta _{d,k}$ är också matroidpolytopen för en enhetlig matroid med $d$ element och rang $k$ .

Exempel

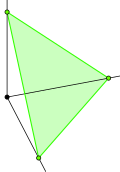
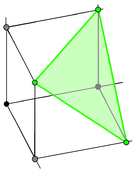
Hypersimplexen $\Delta _{d,1}$ är a $(d-1)$ -simplex (och därför har den $d$ hörn) . Hypersimplex $\Delta _{4,2}$ är en oktaeder , och hypersimplex $\Delta _{5,2}$ är en likriktad 5-cell .

Generellt motsvarar hypersimplexet, ${\displaystyle \Delta _{d,k}} ,$ en enhetlig polytop , som är den $(k-1)$ - rätad $(d-1)$ -dimensionell simplex, med hörn placerade i mitten av alla $(k-1)$ -dimensionella ytor av a $(d-1)$ -dimensionell simplex.

Exempel $(d = 3...6)$
namn	Liksidig triangel	Tetraeder (3-simplex)	Oktaeder	5-celler (4-simplex)	Rättad 5-cell	5-simplex	Rättad 5-simplex	Birektifierad 5-simplex
$Δ d, k = (d, k) = (d, d - k)$	(3,1) (3,2)	(4,1) (4,3)	(4,2)	(5,1) (5,4)	(5,2) (5,3)	(6,1) (6,5)	(6,2) (6,4)	(6,3)
Vertices ${\tbinom {d}{k}}$	3	4	6	5	10	6	15	20
d -koordinater	(0,0,1) (0,1,1)	(0,0,0,1) (0,1,1,1)	(0,0,1,1)	(0,0,0,0,1) (0,1,1,1,1)	(0,0,0,1,1) (0,0,1,1,1)	(0,0,0,0,0,1) (0,1,1,1,1,1)	(0,0,0,0,1,1) (0,0,1,1,1,1)	(0,0,0,1,1,1)
Bild
Grafer	J (3,1) ₌ K2	J (4,1) = K ₃	J (4,2) = T(6,3)	J (5,1) = K ₄	J (5,2)	J (6,1) = K ₅	J (6,2)	J (6,3)
Coxeter diagram
Schläfli symboler	{3} = r {3}	{3,3} = 2 r {3,3}	r{3,3} = {3,4}	{3,3,3} = 3 r {3,3,3}	r {3,3,3} = 2 r { 3,3,3}	{3,3,3,3} = 4 r {3,3,3,3}	r {3,3,3,3} = 3 r {3,3,3,3}	2 r {3,3,3,3}
Fasetter	{ }	{3}		{3,3}	{3,3}, {3,4}	{3,3,3}	{3,3,3}, r {3,3,3}	r {3,3,3}

Historia

Hypersimplicesna studerades först och namngavs i beräkningen av karakteristiska klasser (ett viktigt ämne i algebraisk topologi ), av Gabrièlov, Gelʹfand & Losik (1975) .

Vidare läsning

Hibi, Takayuki; Solus, Liam (2016), "Facets of the r -stable (n , k) -hypersimplex", Annals of Combinatorics , 20 : 815–829, arXiv : 1408.5932 , Bibcode : 2014arXiv1408.5910 ,0200H ,0200H ,02002: 0200s , 02102:7 6 -0325-x .