Isokvant

En isokvantkarta där produktionsutgång Q3 > Q2 > Q1. Vanligtvis skulle indata X och Y hänvisa till arbete respektive kapital. Mer av ingång X, ingång Y eller båda krävs för att flytta från isokvant Q1 till Q2, eller från Q2 till Q3.

A) Exempel på en isokvantkarta med två ingångar som är perfekta substitut.

B) Exempel på en isokvantkarta med två ingångar som är perfekta komplement.

En isokvant (som härrör från kvantitet och det grekiska ordet iso, som betyder lika), i mikroekonomi , är en konturlinje som dras genom uppsättningen av punkter där samma kvantitet av produktion produceras samtidigt som kvantiteterna av två eller flera indata ändras. X- och y-axeln på en isokvant representerar två relevanta indata, som vanligtvis är en produktionsfaktor såsom arbete, kapital, mark eller organisation. En isokvant kan också vara känd som en "Iso-produktkurva" eller en "Equal Product Curve".

Isokvant vs. likgiltighetskurva

Medan en kartläggning av likgiltighetskurvan hjälper till att lösa konsumenternas nyttomaximerande problem, hanterar den isokvanta kartläggningen producenternas kostnadsminimerings- och vinst- och produktionsmaximeringsproblem. Indifferenskurvor skiljer sig vidare från isokvanter genom att de inte kan erbjuda ett exakt mått på nyttan, bara hur det är relevant för en baslinje. Medan produkten från en isokvant kan mätas noggrant i fysiska enheter, och man vet exakt hur mycket isokvant 1 överstiger isokvant 2.

Natur och praktisk användning av en isokvant

Inom förvaltningsekonomi ritas isokvanter vanligtvis tillsammans med isokostkurvor i kapital-arbete-grafer , som visar den tekniska avvägningen mellan kapital och arbete i produktionsfunktionen, och den minskande marginella avkastningen för båda insatserna. Inom företagsekonomi är enheten isokvant vanligtvis nettot av kapitalkostnader. Som sådan lutar isokvanter till sin natur nedåt på grund av driften av minskande marginalnivåer för teknisk substitution ( MRTS). Lutningen av en isokvant representerar hastigheten med vilken ingång x kan ersätta ingång y. Detta koncept är MRTS, så MRTS = lutning av isokvanten. Således, ju brantare isokvanten är, desto högre MRTS. Eftersom MRTS måste minska måste isokvanter vara konvexa till sitt ursprung. Att lägga till en ingång samtidigt som den andra hålls konstant leder så småningom till minskande marginell produktion.

Konturlinjen för en isokvant representerar varje kombination av två indata som fullt ut maximerar ett företags användning av resurser (som budget eller tid). Full maximering av resurser anses vanligtvis vara "effektiv". Effektiv allokering av produktionsfaktorer sker endast när två isokvanter tangerar varandra. Om ett företag producerar till vänster om konturlinjen, anses företaget vara ineffektivt eftersom de inte maximerar användningen av sina tillgängliga resurser. Ett företag kan inte producera till höger om konturlinjen om de inte överskrider sina begränsningar.

D) Produktionsisokvant (strikt konvex) och isokostkurva (linjär)

En familj av isokvanter kan representeras av en isokvantkarta , en graf som kombinerar ett antal isokvanter, som var och en representerar olika mängder utdata. En isokvantkarta kan indikera minskande eller ökande skalåtergång baserat på ökande eller minskande avstånd mellan isokvantparen av fast uteffektökning, när uteffekten ökar. Om avståndet mellan dessa isokvanter ökar när produktionen ökar, uppvisar företagets produktionsfunktion minskande skalavkastning; dubblering av båda ingångarna kommer att resultera i placering på en isokvant med mindre än dubbelt så stor utdata som den föregående isokvanten. Omvänt, om avståndet minskar när produktionen ökar, upplever företaget ökande skalavkastning; dubblering av båda ingångarna resulterar i placering på en isokvant med mer än dubbelt så stor utdata som den ursprungliga isokvanten. Ett företag kan välja att använda den information en isokvant ger om avkastning till skala , genom att använda den som insikt i hur man fördelar resurser.

C) Isokvant 1 är mycket mer input-Y-intensiv än isokvant 2.

Att veta hur man fördelar resurser är ett begrepp som är relevant för företagsekonomi. Isokvanter kan vara användbara för att grafiskt representera problemet med knapphet . De visar i vilken utsträckning företaget i fråga har förmågan att substituera mellan två olika indata (x och y i grafen) efter behag för att producera samma nivå av produktion (se: Diagram C)). De representerar också olika kvantitetskombinationer av två varor som följer en budgetrestriktion . Således kan de användas som ett verktyg för att hjälpa ledningen att fatta bättre informerade beslut angående produktions- och vinstdilemman, såsom kostnads- eller avfallsminimering och maximering av intäkter och produktion.

Ett företag kan bestämma den lägsta kostnadskombinationen av insatsvaror för att producera en given produktion, genom att kombinera isokostkurvor och isokvanter, och följa First Order Conditions . Den lägsta kostnadskombinationen är där förhållandet mellan marginalprodukter är lika med förhållandet mellan faktorpriser. Vid denna punkt kommer isokvantens lutning och isokostens lutning att vara lika (se skärningspunkten för graf D). Ett företag har incitament att producera till den lägsta kostnadskombinationen eftersom det är vid denna tidpunkt de relaterade kostnaderna för önskad produktion minimeras.

Som med indifferenskurvor kan två isokvanter aldrig korsas. Dessutom är alla möjliga kombinationer av ingångar på en isokvant. Slutligen representerar varje kombination av ingångar ovanför eller till höger om ett isokvantresultat en högre utmatningsnivå och vice versa. Även om marginalprodukten av en insats minskar när du ökar mängden insats samtidigt som alla andra insatser hålls konstanta, är marginalprodukten aldrig negativ i det empiriskt observerade intervallet eftersom ett rationellt företag aldrig skulle öka en insats för att minska produktionen .

Former av en isokvant

Om de två ingångarna är perfekta substitut, representeras den resulterande isokvantkartan som genereras i fig. A; med en given produktionsnivå Q3 kan insats X ersättas med insats Y i oföränderlig takt. De perfekta ersättningsinsatserna upplever inte sjunkande marginalavkastning när de ersätts med varandra i produktionsfunktionen.

Om de två ingångarna är perfekta komplement har isokvantkartan formen av fig. B; med en produktionsnivå Q3 kan input X och input Y endast kombineras effektivt i det vissa förhållande som uppstår vid kinken i isokvanten. Företaget kommer att kombinera de två insatserna i det nödvändiga förhållandet för att maximera vinsten.

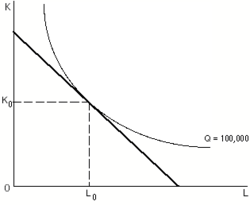
Isokvanter kombineras vanligtvis med isokostlinjer för att lösa ett kostnadsminimeringsproblem för en given produktionsnivå. I det typiska fallet som visas i den översta figuren, med jämnt krökta isokvanter, kommer ett företag med fasta enhetskostnader för insatsvarorna att ha isokostkurvor som är linjära och nedåtlutande; varje tangenspunkt mellan en isokvant och en isokostkurva representerar den kostnadsminimerande ingångskombinationen för att producera den utmatningsnivå som är associerad med den isokvanten. En linje som förenar tangenspunkter för isokvanter och isokostnader (med insatspriser hållna konstanta) kallas expansionsvägen .

Icke konvexitet

Under antagandet om en sjunkande marginalgrad för teknisk substitution, och därmed en positiv och finit substitutionselasticitet, är isokvanten konvex mot ursprunget. En lokalt icke-konvex isokvant kan uppstå om det finns tillräckligt starka skalåtergångar i en av ingångarna. I det här fallet finns det en negativ substitutionselasticitet - när förhållandet mellan insats A och insats B ökar, ökar marginalprodukten av A i förhållande till B snarare än minskar.

En icke-konvex isokvant är benägen att producera stora och diskontinuerliga förändringar i den prisminimerande insatsmixen som svar på prisförändringar. Betrakta till exempel fallet där isokvanten är globalt ickekonvex och isokostkurvan är linjär. I det här fallet kommer den lägsta kostnadsmixen av insatser att vara en hörnlösning, och inkluderar endast en ingång (till exempel antingen ingång A eller ingång B). Valet av vilken insats som ska användas beror på de relativa priserna. Vid något kritiskt prisförhållande kommer den optimala insatsmixen att skifta från all insats A till all insats B och vice versa som svar på en liten förändring i relativa priser.

Se även

• Mikroekonomi
• Produktion, kostnader och prissättning
• Grunderna i produktionsteori
• Marginalgraden för teknisk substitution
• Lerner diagram
• Budgetrestriktion