Intraklasskorrelation

En punktplot som visar en datauppsättning med hög intraklasskorrelation. Värden från samma grupp tenderar att vara likartade.

En punktplot som visar en datauppsättning med låg intraklasskorrelation. Det finns ingen tendens att värderingar från samma grupp är lika.

Inom statistik är intraklasskorrelationen , eller intraklasskorrelationskoefficienten ( ICC ) , en beskrivande statistik som kan användas när kvantitativa mätningar görs på enheter som är organiserade i grupper. Den beskriver hur starkt enheter i samma grupp liknar varandra. Även om det ses som en typ av korrelation , fungerar det till skillnad från de flesta andra korrelationsmått på data strukturerad som grupper snarare än data strukturerad som parade observationer.

Intraklasskorrelationen används vanligen för att kvantifiera i vilken grad individer med en bestämd grad av släktskap (t.ex. helsyskon) liknar varandra i termer av en kvantitativ egenskap (se ärftlighet ) . En annan framträdande tillämpning är bedömningen av konsistens eller reproducerbarhet av kvantitativa mätningar gjorda av olika observatörer som mäter samma kvantitet.

Tidig ICC-definition: opartisk men komplex formel

Det tidigaste arbetet med intraklasskorrelationer fokuserade på fallet med parade mätningar, och den första statistiken för intraklasskorrelation (ICC) som föreslås var modifieringar av interklasskorrelationen ( Pearson -korrelation).

Betrakta en datamängd som består av N parade datavärden ( x _{n ,1} , x _{n ,2} ), för n = 1, ..., N . Intraklasskorrelationen r som ursprungligen föreslogs av Ronald Fisher är

r={\frac {1}{Ns^{2}}}\ summa _{n=1}^{N}(x_{n,1}-{\bar {x}})(x_{n,2}-{\bar {x}}),

var

{\bar {x}}={\frac {1}{2N}}\summa _{n= 1}^{N}(x_{n,1}+x_{n,2}),

s^{2}={\frac {1}{2N}}\left\{\sum _{n=1}^{N}(x_{n,1}-{\bar {x}} )^{2}+\summa _{n=1}^{N}(x_{n,2}-{\bar {x}})^{2}\right\}.

Senare versioner av denna statistik använde frihetsgraderna 2 N −1 i nämnaren för att beräkna s ² och N −1 i nämnaren för att beräkna r , så att s ² blir opartisk och r blir opartisk om s är känt.

Den viktigaste skillnaden mellan denna ICC och interklasskorrelationen ( Pearson) är att data poolas för att uppskatta medelvärdet och variansen. Anledningen till detta är att i den miljö där en intraklasskorrelation önskas anses paren vara oordnade. Till exempel, om vi studerar likheten mellan tvillingar, finns det vanligtvis inget meningsfullt sätt att ordna värdena för de två individerna inom ett tvillingpar. Liksom interklasskorrelationen kommer intraklasskorrelationen för parade data att begränsas till intervallet [ −1 , +1].

Intraklasskorrelationen definieras också för datamängder med grupper som har fler än 2 värden. För grupper som består av tre värden definieras det som

r={\frac {1}{3Ns^{2}}}\sum _{n=1}^{ N}\vänster\{(x_{n,1}-{\bar {x}})(x_{n,2}-{\bar {x}})+(x_{n,1}-{\bar {x}})(x_{n,3}-{\bar {x}})+(x_{n,2}-{\bar {x}})(x_{n,3}-{\bar { x}})\right\},

var

{\bar {x}}={\frac {1}{3N}}\ summa _{n=1}^{N}(x_{n,1}+x_{n,2}+x_{n,3}),

s^{2}={\frac {1}{3N}}\left\{\sum _{n=1}^{N}(x_{n,1}-{\bar {x}} )^{2}+\summa _{n=1}^{N}(x_{n,2}-{\bar {x}})^{2}+\summa _{n=1}^{N }(x_{n,3}-{\bar {x}})^{2}\right\}.

I takt med att antalet artiklar per grupp växer, ökar också antalet produkttermer i detta uttryck. Följande motsvarande form är enklare att beräkna:

r={\frac {K}{K-1}}\ cdot {\frac {N^{-1}\sum _{n=1}^{N}({\bar {x}}_{n}-{\bar {x}})^{2}}{ s^{2}}}-{\frac {1}{K-1}},

där K är antalet datavärden per grupp, och ${\bar {x}}_{n}$ är provmedelvärdet för den n ^:te gruppen. Denna form tillskrivs vanligtvis Harris . Den vänstra termen är icke-negativ; följaktligen måste intraklasskorrelationen uppfyllas

r\geq {\frac {-1}{K-1}}.

För stort K är detta ICC nästan lika med

{\frac {N^{-1}\sum _{n=1}^{N}({\bar { x}}_{n}-{\bar {x}})^{2}}{s^{2}}},

vilket kan tolkas som den bråkdel av den totala variansen som beror på variation mellan grupper. Ronald Fisher ägnar ett helt kapitel åt intraklasskorrelation i sin klassiska bok Statistical Methods for Research Workers .

För data från en population som är fullständigt brus ger Fishers formel ICC-värden som är fördelade på cirka 0, dvs ibland negativa. Detta beror på att Fisher utformade formeln för att vara opartisk, och därför är dess uppskattningar ibland överskattningar och ibland underskattningar. För små eller 0 underliggande värden i populationen kan ICC beräknat från ett urval vara negativt.

Moderna ICC-definitioner: enklare formel men positiv bias

Från och med Ronald Fisher har intraklasskorrelationen betraktats inom ramen för variansanalys (ANOVA), och på senare tid inom ramen för slumpmässiga effektmodeller . Ett antal ICC-uppskattare har föreslagits. De flesta av estimatorerna kan definieras i termer av modellen för slumpmässiga effekter

Y_{ij}=\mu +\alpha _{j}+\varepsilon _{ij},

där Y _ij är den i: ^te observationen i den j: ^te gruppen, μ är ett oobserverat övergripande medelvärde , α _{j är en oobserverad} εij _slumpmässig effekt som delas av alla värden i grupp j , och är en oobserverad brusterm. För att modellen ska identifieras α _j och ε _ij ha förväntat värde noll och vara okorrelerade med varandra. Dessutom αj _. vara identiskt fördelade och ε _ij antas vara identiskt fördelade Variansen för α _j betecknas σ
²_α och variansen för ε _ij betecknas σ
²_ε .

Befolkningen ICC i detta ramverk är

{\frac {\sigma _{\alpha }^{2}}{\sigma _{\alpha }^{2}+\sigma _{\varepsilon }^{2}}}.

Med detta ramverk är ICC korrelationen av två observationer från samma grupp.

[Bevis]

För en enkelriktad modell för slumpmässiga effekter:

$Y_{ij}=\mu +\alpha _{i}+\epsilon _{ij}$

$\alpha _{i}\sim N(0,\sigma _{\alpha }^{2})$ , ${ \displaystyle \epsilon _{ij}\sim N(0,\sigma ^{2})} ,$ α $\displaystyle \alpha _{i}}$ s och $\epsilon _{ij}$ s oberoende och $\alpha _{i}$ s är oberoende av $\epsilon _{ij}$ s.

Variansen för varje observation är: $Var(Y_{ij})=\sigma ^{2}+\sigma _{\alpha }^{2 }$ Kovariansen för två observationer från samma grupp i (för ${\displaystyle j\neq k} )$ är:

${\begin{aligned}{\text{Cov}}(Y_{ij},Y_{ik})&={\text{Cov}}(\mu +\alpha _{i}+\epsilon _ {ij},\mu +\alpha _{i}+\epsilon _{ik})\\&={\text{Cov}}(\alpha _{i}+\epsilon _{ij},\alpha _ {i}+\epsilon _{ik})={\text{Cov}}(\alpha _{i},\alpha _{i})+2{\text{Cov}}(\alpha _{i} ,\epsilon _{ik})+{\text{Cov}}(\epsilon _{ij},\epsilon _{ik})\\&={\text{Cov}}(\alpha _{i}, \alpha _{i})={\text{Var}}(\alpha _{i})\\&=\sigma _{\alpha }^{2}.\\\end{aligned}}$

I detta har vi använt egenskaperna för kovariansen .

Tillsammans får vi: ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha } ^{2}}}$

En fördel med detta ANOVA-ramverk är att olika grupper kan ha olika antal datavärden, vilket är svårt att hantera med den tidigare ICC-statistiken. Denna ICC är alltid icke-negativ, vilket gör att den kan tolkas som andelen av total varians som är "mellan grupper". Denna ICC kan generaliseras för att möjliggöra kovariateffekter, i vilket fall ICC tolkas som att den fångar likheten inom klassen för de kovariatjusterade datavärdena.

Detta uttryck kan aldrig vara negativt (till skillnad från Fishers ursprungliga formel) och därför, i prover från en population som har en ICC på 0, kommer ICC i proverna att vara högre än ICC för populationen.

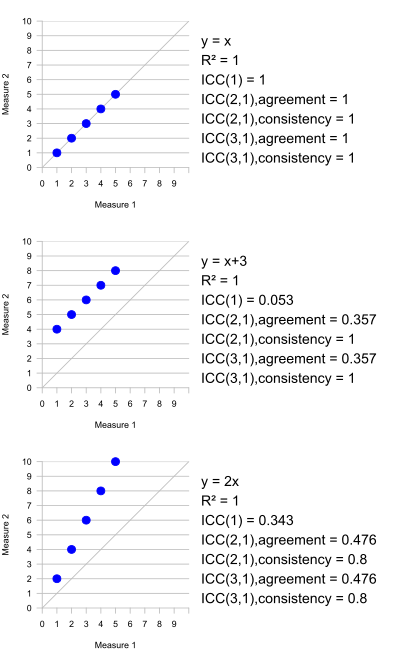
Ett antal olika ICC-statistik har föreslagits, som inte alla uppskattar samma populationsparameter. Det har varit stor debatt om vilken ICC-statistik som är lämplig för en viss användning, eftersom den kan ge markant olika resultat för samma data.

Förhållande till Pearsons korrelationskoefficient

När det gäller dess algebraiska form är Fishers ursprungliga ICC den ICC som mest liknar Pearson-korrelationskoefficienten . En viktig skillnad mellan de två statistiken är att i ICC centreras och skalas data med hjälp av ett poolat medelvärde och standardavvikelse, medan i Pearson-korrelationen är varje variabel centrerad och skalad med sitt eget medelvärde och standardavvikelse. Denna poolade skalning för ICC är vettig eftersom alla mätningar är av samma kvantitet (om än på enheter i olika grupper). Till exempel i en parad datamängd där varje "par" är en enda mätning gjord för var och en av två enheter (t.ex. vägning av varje tvilling i ett par identiska tvillingar) snarare än två olika mätningar för en enda enhet (t.ex. mätning av höjd och vikt för varje individ), är ICC ett mer naturligt mått på association än Pearsons korrelation.

En viktig egenskap hos Pearson-korrelationen är att den är oföränderlig vid tillämpning av separata linjära transformationer på de två variablerna som jämförs. Således, om vi korrelerar X och Y , där säg Y = 2 X + 1, är Pearson-korrelationen mellan X och Y 1 - en perfekt korrelation. Den här egenskapen är inte meningsfull för ICC, eftersom det inte finns någon grund för att bestämma vilken transformation som tillämpas på varje värde i en grupp. Men om all data i alla grupper utsätts för samma linjära transformation, ändras inte ICC.

Används för att bedöma överensstämmelse bland observatörer

ICC används för att bedöma överensstämmelsen, eller överensstämmelsen, hos mätningar gjorda av flera observatörer som mäter samma kvantitet. Till exempel, om flera läkare ombeds bedöma resultaten av en datortomografi för tecken på cancerprogression, kan vi fråga hur konsekventa poängen är för varandra. Om sanningen är känd (till exempel om datortomografin gällde patienter som senare genomgick explorativ kirurgi), så skulle fokus i allmänhet ligga på hur väl läkarnas resultat matchade sanningen. Om sanningen inte är känd kan vi bara överväga likheten mellan poängen. En viktig aspekt av detta problem är att det finns både inter-observatör och intra-observatör variabilitet. Variabilitet mellan observatörer hänvisar till systematiska skillnader mellan observatörerna - till exempel kan en läkare konsekvent poängsätta patienter på en högre risknivå än andra läkare. Variabilitet inom observatören hänvisar till avvikelser av en viss observatörs poäng på en viss patient som inte är en del av en systematisk skillnad.

ICC är konstruerad för att tillämpas på utbytbara mätningar - det vill säga grupperade data där det inte finns något meningsfullt sätt att ordna mätningarna inom en grupp. Vid bedömning av överensstämmelse mellan observatörer, om samma observatörer betygsätter varje element som studeras, kommer det sannolikt att finnas systematiska skillnader mellan observatörer, vilket strider mot begreppet utbytbarhet. Om ICC används i en situation där systematiska skillnader finns, är resultatet ett sammansatt mått på variabilitet mellan observatörer och mellan observatörer. En situation där utbytbarhet rimligen kan antas hålla skulle vara när ett prov som ska poängsättas, säg ett blodprov, delas upp i flera alikvoter och alikvoterna mäts separat på samma instrument. I det här fallet skulle utbytbarheten vara kvar så länge som ingen effekt på grund av sekvensen för att köra proverna var närvarande.

Eftersom intraklasskorrelationskoefficienten ger en sammansättning av intra-observatörs- och inter-observatörsvariabilitet, anses dess resultat ibland vara svårtolkade när observatörerna inte är utbytbara. Alternativa mått såsom Cohens kappa-statistik , Fleiss kappa och konkordanskorrelationskoefficienten har föreslagits som mer lämpliga mått på överensstämmelse bland icke-utbytbara observatörer.

Beräkning i mjukvarupaket

Olika definitioner av intraklasskorrelationskoefficient tillämpas på tre scenarier av inter-observatörskonkordans.

ICC stöds i mjukvarupaketet R med öppen källkod (med funktionen "icc" med paketen psy eller irr , eller via funktionen "ICC" i paketet psych .) Paketet rptR tillhandahåller metoder för uppskattning av ICC och repeterbarheter för Gaussisk, binomial och Poisson distribuerade data i ett ramverk med blandade modeller. Speciellt tillåter paketet uppskattning av justerad ICC (dvs. att kontrollera för andra variabler) och beräknar konfidensintervall baserat på parametrisk bootstrapping och signifikanser baserat på permutation av residualer. Kommersiell programvara stöder även ICC, till exempel Stata eller SPSS

Olika typer av ICC [3] Arkiverad 2009-03-03 på Wayback Machine
Shrout och Fleiss konvention	McGraw och Wong-konventionen	Namn i SPSS och Stata
ICC(1,1)	Enkelriktad slumpmässig, enkel poäng ICC(1)	Enkelriktade slumpmässiga, enstaka mått
ICC(2,1)	Tvåvägs slumpmässig, enkel poäng ICC(A,1)	Tvåvägs slumpmässiga, enstaka mått, absolut överensstämmelse
ICC(3,1)	Tvåvägs blandad, enkel poäng ICC(C,1)	Tvåvägsmixad, enstaka mått, konsistens
odefinierad	Tvåvägs slumpmässig, enkel poäng ICC(C,1)	Tvåvägs slumpmässiga, enstaka mått, konsekvens
odefinierad	Tvåvägs blandad, enkel poäng ICC(A,1)	Tvåvägs blandade, enstaka åtgärder, absolut överensstämmelse
ICC(1,k)	Enkelriktad slumpmässig, genomsnittlig poäng ICC(k)	Enkelriktade slumpmässiga medelmått
ICC(2,k)	Tvåvägs slumpmässig, genomsnittlig poäng ICC(A,k)	Tvåvägs slumpmässiga, genomsnittliga mått, absolut överensstämmelse
ICC(3,k)	Tvåvägs blandad, genomsnittlig poäng ICC(C,k)	Tvåvägs blandade, genomsnittliga mått, konsistens
odefinierad	Tvåvägs slumpmässig, genomsnittlig poäng ICC(C,k)	Tvåvägs slumpmässiga, genomsnittliga mått, konsekvens
odefinierad	Tvåvägs blandad, genomsnittlig poäng ICC(A,k)	Tvåvägs blandade, genomsnittliga mått, absolut överensstämmelse

De tre modellerna är:

Enkelriktade slumpmässiga effekter: varje individ mäts av en annan uppsättning k slumpmässigt utvalda bedömare;
Tvåvägsslumpmässigt: k-bedömare väljs slumpmässigt, sedan mäts varje individ av samma uppsättning k-bedömare;
Tvåvägs blandade: k fasta bedömare definieras. Varje ämne mäts av k-bedömarna.

Antal mätningar:

Enstaka mått: även om mer än en åtgärd vidtas i experimentet, appliceras tillförlitlighet på ett sammanhang där en enstaka mätning av en enskild bedömare kommer att utföras;
Genomsnittliga mått: tillförlitligheten tillämpas på ett sammanhang där mått på k-bedömare beräknas i medeltal för varje ämne.

Konsekvens eller absolut överensstämmelse:

Absolut överensstämmelse: överenskommelsen mellan två bedömare är av intresse, inklusive systematiska fel hos båda bedömarna och slumpmässiga restfel;
Konsistens: i samband med upprepade mätningar av samma bedömare, raderas systematiska fel hos bedömaren och endast det slumpmässiga kvarvarande felet behålls.

Konsistensen ICC kan inte uppskattas i envägsmodellen för slumpmässiga effekter, eftersom det inte finns något sätt att separera inter-rater och kvarvarande varianser.

En översikt och omanalys av de tre modellerna för de enskilda måtten ICC, med ett alternativt recept för deras användning, har också presenterats av Liljequist et al (2019).

Tolkning

Cicchetti (1994) ger följande ofta citerade riktlinjer för tolkning för åtgärder för kappa eller ICC:s interbedömare:

Mindre än 0,40—dåligt.
Mellan 0,40 och 0,59 — rättvist.
Mellan 0,60 och 0,74 - bra.
Mellan 0,75 och 1,00 — utmärkt.

En annan riktlinje ges av Koo och Li (2016):

under 0,50: dålig
mellan 0,50 och 0,75: måttlig
mellan 0,75 och 0,90: bra
över 0,90: utmärkt

Se även

Andra

En jämförelse av två index för intraklasskorrelationskoefficienten

externa länkar