Ikosaedrisk pyramid
| Icosahedral pyramid | ||
|---|---|---|
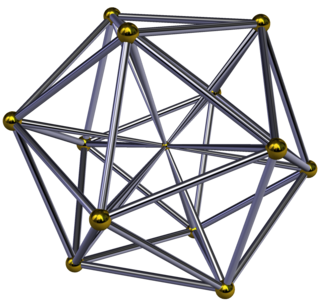 Schlegel diagram |
||
| Typ | Polyedrisk pyramid | |
| Schläfli symbol | ( ) ∨ {3,5} | |
| Celler | 21 | 1 {3,5} 20 ( ) ∨ {3} |
| Ansikten | 50 | 20+30 {3} |
| Kanter | 12+30 | |
| Vertices | 13 | |
| Dubbel | Dodekaedrisk pyramid | |
| Symmetrigrupp | H3 , [5,3,1] , ordning 120 | |
| Egenskaper | konvexa , regelbundna celler, Blind polytop | |
Den icosahedriska pyramiden är en fyrdimensionell konvex polytop , begränsad av en icosahedron som bas och av 20 triangulära pyramidceller som möts vid dess spets. Eftersom en ikosaeders cirkumradius är mindre än dess kantlängd, kan de tetraedriska pyramiderna göras med regelbundna ytor.
Med alla vanliga celler är det en blind polytop . Två kopior kan utökas för att göra en ikosaedrisk bipyramid som också är en blind polytop.
Den vanliga 600-cellen har ikosaedriska pyramider runt varje vertex.
Dualen till den icosaedriska pyramiden är den dodekaedriska pyramiden , sedd som en dodekaedrisk bas, och 12 vanliga femkantiga pyramider som möts vid en spets.
externa länkar
- Olshevsky, George. "Pyramid" . Ordlista för Hyperspace . Arkiverad från originalet den 4 februari 2007.
-
Klitzing, Richard. "4D Segmentotoper" .
- Klitzing, Richard. "Segmentotop ikepy, K-4.84" .
- Richard Klitzing, Axial-Symmetrical Edge Facets of Uniform Polyhedra
- Ikosaedrisk pyramid
Kategorier:
