Hough transformera
| Funktionsdetektering |
|---|
| Kantdetektering |
| Hörndetektering |
| Blob-detektering |
| Åsdetektering |
| Hough transformation |
| Strukturtensor |
| Affin invariant funktionsdetektion |
| Funktionsbeskrivning |
| Skala utrymme |
Hough -transformen är en funktionsextraktionsteknik som används vid bildanalys , datorseende och digital bildbehandling . Syftet med tekniken är att hitta ofullkomliga förekomster av objekt inom en viss klass av former genom en omröstningsprocedure. Denna omröstningsprocedure utförs i ett parameterutrymme , från vilket objektkandidater erhålls som lokala maxima i ett så kallat ackumulatorutrymme som är explicit konstruerat av algoritmen för beräkning av Hough-transformen.
Den klassiska Hough-transformen handlade om identifieringen av linjer i bilden, men senare har Hough-transformen utökats till att identifiera positioner av godtyckliga former, oftast cirklar eller ellipser . Hough-transformen som den används allmänt idag uppfanns av Richard Duda och Peter Hart 1972, som kallade den en "generaliserad Hough-transform" efter det relaterade patentet från 1962 av Paul Hough. Förvandlingen populariserades i datorseendegemenskapen av Dana H. Ballard genom en tidskriftsartikel från 1981 med titeln " Generalisering av Hough-transformen för att upptäcka godtyckliga former" .
Historia
Det uppfanns ursprungligen för maskinanalys av bubbelkammarfotografier (Hough, 1959).
Hough-transformen patenterades som US-patent 3 069 654 1962 och tilldelades US Atomic Energy Commission med namnet "Method and Means for Recognizing Complex Patterns". Detta patent använder en parametrisering av lutningsavsnitt för raka linjer, vilket obekvämt leder till ett obegränsat transformationsutrymme eftersom lutningen kan gå till oändlighet.
Den rho-theta-parametrisering som används universellt idag beskrevs först i
- Duda, RO; Hart, PE (januari 1972). "Användning av Hough-transformationen för att upptäcka linjer och kurvor i bilder". Comm. ACM . 15 : 11–15. doi : 10.1145/361237.361242 . S2CID 1105637 .
även om det redan var standard för Radon-transformen sedan åtminstone 1930-talet.
O'Gorman och Clowes variation beskrivs i
- O'Gorman, Frank; Clowes, MB (1976). "Hitta bildkanter genom kollinearitet av funktionspunkter". IEEE Trans. Comput . 25 (4): 449–456. doi : 10.1109/TC.1976.1674627 . S2CID 10851078 .
Historien om hur den moderna formen av Hough-transformen uppfanns ges in
- Hart, PE (november 2009). "Hur Hough Transform uppfanns" (PDF) . IEEE Signal Processing Magazine . 26 (6): 18–22. doi : 10.1109/msp.2009.934181 . S2CID 16245096 . Arkiverad från originalet (PDF) 2018-05-16.
Teori
Vid automatiserad analys av digitala bilder uppstår ofta ett delproblem med att upptäcka enkla former, såsom raka linjer, cirklar eller ellipser. I många fall kan en kantdetektor användas som ett förbearbetningssteg för att erhålla bildpunkter eller bildpixlar som ligger på den önskade kurvan i bildrymden. På grund av ofullkomligheter i antingen bilddata eller kantdetektorn kan det dock saknas punkter eller pixlar på de önskade kurvorna såväl som rumsliga avvikelser mellan den ideala linjen/cirkeln/ellipsen och de brusiga kantpunkterna när de erhålls från kantdetektor. Av dessa skäl är det ofta icke-trivialt att gruppera de extraherade kantdelarna till en lämplig uppsättning linjer, cirklar eller ellipser. Syftet med Hough-transformen är att ta itu med detta problem genom att göra det möjligt att utföra grupperingar av kantpunkter till objektkandidater genom att utföra en explicit röstningsprocedur över en uppsättning parametriserade bildobjekt (Shapiro och Stockman, 304).
Upptäcker linjer
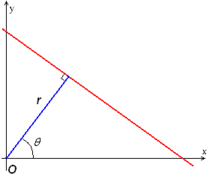
Det enklaste fallet med Hough-transform är att upptäcka raka linjer. I allmänhet kan den räta linjen y = mx + b representeras som en punkt ( b , m ) i parameterutrymmet. Men vertikala linjer utgör ett problem. De skulle ge upphov till obegränsade värden för lutningsparametern m . Sålunda, av beräkningsskäl, föreslog Duda och Hart användningen av Hessens normala form
där är avståndet från origo till närmaste punkt på den räta linjen, och är vinkeln mellan -axeln och linjen som förbinder origo med det närmaste punkt.
Intuitionen för denna form, i likhet med planekvationen, är att varje vektor på linjen måste vara vinkelrät (ortogonal) mot den raka längden r {\ som kommer från origo. Det är lätt att se att skärningspunkten för funktionslinjen och den vinkelräta linjen som kommer från origo ligger vid . Så för varje punkt på linjen måste vektorn vara ortogonal mot vektorn . Därför får vi att för vilken punkt på funktionsraden, ekvationen måste vara uppfylld. Därför . Eftersom och , vi får . Eftersom , får vi den slutliga formen av .
Det är därför möjligt att associera till varje rad i bilden ett par . Planet kallas ibland Hough-utrymme för uppsättningen raka linjer i två dimensioner. Denna representation gör Hough-transformen konceptuellt mycket nära den tvådimensionella Radontransformen . Faktum är att Hough-transformen är matematiskt likvärdig med Radon-transformationen, men de två transformationerna har olika beräkningstolkningar som traditionellt är förknippade med dem.
Givet en enda punkt i planet, motsvarar uppsättningen av alla räta linjer som går genom den punkten en sinusformad kurva i ( r , θ )-planet, vilket är unikt för den punkten. En uppsättning av två eller flera punkter som bildar en rät linje kommer att producera sinusoider som korsar vid ( r , θ ) för den linjen. Således kan problemet med att detektera kolinjära punkter omvandlas till problemet med att hitta samtidiga kurvor .
Probabilistisk tolkning
Givet en form parametriserad av , tar värden i mängden som kallas formen utrymme, kan man tolka Hough-transformen som den omvända transformationen av en sannolikhetsfördelning på bildrymden till formutrymmet och tolka formdetektering som maximal sannolikhetsuppskattning .
Explicit utför Hough-transformen en ungefärlig naiv Bayes- slutledning. Vi börjar med en enhetlig prior på formutrymmet. Vi tar bara hänsyn till de positiva bevisen och ignorerar alla negativa bevis, så att vi kan upptäcka delvis tilltäppta former.
Vi summerar logsannolikheten i formutrymmet till en additiv konstant. Antagandet om naiva Bayes innebär att alla pixlar i bildrummet ger oberoende bevis, så att deras sannolikheter multipliceras, det vill säga deras log-sannolikheter adderas. Friheten i additiv konstant tillåter oss att inte utföra någon operation på "bakgrundspixlarna" i formrymden.
Slutligen utför vi maximal sannolikhetsuppskattning genom att plocka ut topparna i logsannolikheten på formutrymmet.
Genomförande
Den linjära Hough-transformeringsalgoritmen uppskattar de två parametrarna som definierar en rät linje. Transformutrymmet har två dimensioner, och varje punkt i transformationsutrymmet används som en ackumulator för att detektera eller identifiera en linje som beskrivs av . Varje punkt i de upptäckta kanterna i bilden bidrar till ackumulatorerna.
Dimensionen på ackumulatorn är lika med antalet okända parametrar, dvs två, med tanke på kvantiserade värden på och i paret . För varje pixel vid och dess grannskap, bestämmer Hough-transformeringsalgoritmen om det finns tillräckligt med bevis för en rät linje vid den pixeln. Om så är fallet kommer den att beräkna parametrarna för den raden, leta sedan efter ackumulatorns fack som parametrarna faller in i och öka värdet på det facket.
Genom att hitta lagerplatserna med de högsta värdena, typiskt genom att leta efter lokala maxima i ackumulatorutrymmet, kan de mest sannolika linjerna extraheras och deras (ungefärliga) geometriska definitioner läsas av (Shapiro och Stockman, 304). Det enklaste sättet att hitta dessa toppar är genom att tillämpa någon form av tröskel, men andra tekniker kan ge bättre resultat under olika omständigheter – att avgöra vilka linjer som hittas, såväl som hur många. Eftersom de returnerade linjerna inte innehåller någon längdinformation är det ofta nödvändigt att i nästa steg hitta vilka delar av bilden som stämmer överens med vilka linjer. Dessutom, på grund av ofullkomlighetsfel i kantdetekteringssteget, kommer det vanligtvis att finnas fel i ackumulatorutrymmet, vilket kan göra det icke-trivialt att hitta de lämpliga topparna, och därmed de lämpliga linjerna.
Det slutliga resultatet av den linjära Hough-transformen är en tvådimensionell matris (matris) som liknar ackumulatorn – en dimension av denna matris är den kvantiserade vinkeln θ {\displaystyle \ , och den andra dimensionen är det kvantiserade avståndet . Varje element i matrisen har ett värde lika med summan av de punkter eller pixlar som är placerade på linjen som representeras av kvantiserade parametrar ( . Så elementet med det högsta värdet indikerar den räta linjen som är mest representerad i inmatningsbilden.
Exempel
Exempel 1
Betrakta tre datapunkter, som här visas som svarta prickar.
- För varje datapunkt ritas ett antal linjer genom den, alla i olika vinklar. Dessa visas här i olika färger.
- Hough-transformen ackumulerar bidrag från alla pixlar i den detekterade kanten. Till varje linje finns en stödlinje som är vinkelrät mot den och som skär origo . I varje fall visas en av dessa som en pil.
- Längden (dvs. vinkelrätt avstånd till origo) och vinkeln för varje stödlinje beräknas. Längder och vinklar är tabellerade under diagrammen.
Av beräkningarna kan man se att i båda fallen har stödlinjen vid 60° en liknande längd. Därför är det underförstått att motsvarande linjer (de blåa på bilden ovan) är mycket lika. Man kan alltså anta att alla punkter ligger nära den blå linjen.
Exempel 2
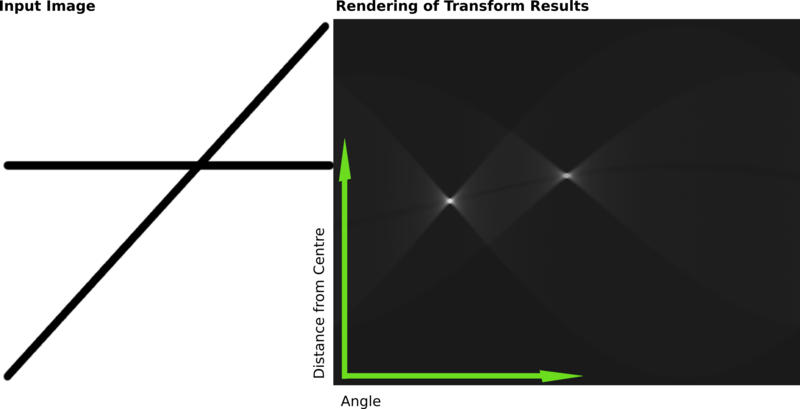
Följande är ett annat exempel som visar resultaten av en Hough-transformation på en rasterbild som innehåller två tjocka linjer.
Resultaten av denna transformation lagrades i en matris. Cellvärdet representerar antalet kurvor genom vilken punkt som helst. Högre cellvärden görs ljusare. De två distinkt ljusa fläckarna är Hough-parametrarna för de två linjerna. Från dessa fläckars positioner kan vinkel och avstånd från bildens centrum för de två linjerna i inmatningsbilden bestämmas.
Variationer och förlängningar
Använda gradientriktningen för att minska antalet röster
En förbättring som föreslagits av O'Gorman och Clowes kan användas för att detektera linjer om man tar hänsyn till att den lokala gradienten för bildintensiteten nödvändigtvis kommer att vara ortogonal mot kanten. Eftersom kantdetektering i allmänhet innefattar beräkning av intensitetsgradientens storlek, hittas gradientriktningen ofta som en bieffekt. Om en given koordinatpunkt ( x,y ) råkar vara på en linje, så ger den lokala riktningen av gradienten θ -parametern som motsvarar nämnda linje, och parametern r erhålls då omedelbart. (Shapiro och Stockman, 305) Gradientriktningen kan uppskattas till inom 20°, vilket förkortar sinuskurvan från hela 180° till ungefär 45°. Detta minskar beräkningstiden och har den intressanta effekten att antalet värdelösa röster minskar, vilket förbättrar synligheten för spikarna som motsvarar verkliga linjer i bilden.
Kärnbaserad Hough-transform (KHT)
Fernandes och Oliveira föreslog ett förbättrat röstningsschema för Hough-transformeringen som gör att en mjukvaruimplementering kan uppnå realtidsprestanda även på relativt stora bilder (t.ex. 1280×960). Den kärnbaserade Hough-transformen använder samma parameterisering som föreslagits av Duda och Hart men arbetar på kluster med ungefär kolinjära pixlar. För varje kluster avges röster med hjälp av en orienterad elliptisk-gaussisk kärna som modellerar osäkerheten förknippad med den bäst passande linjen med avseende på motsvarande kluster. Tillvägagångssättet förbättrar inte bara avsevärt prestandan för röstningssystemet, utan producerar också en mycket renare ackumulator och gör transformationen mer robust för detektering av falska linjer.
3D-kärnbaserad Hough-transform för plandetektering (3DKHT)
Limberger och Oliveira föreslog en deterministisk teknik för plandetektering i oorganiserade punktmoln vars kostnad är i antalet prover, för att uppnå realtidsprestanda för relativt stora datamängder (uppåt till punkter på en 3,4 GHz CPU). Den är baserad på en snabb Hough-transform-röstningsstrategi för plana regioner, inspirerad av den kärnbaserade Hough-transformen (KHT). Denna 3D-kärnbaserade Hough-transform (3DKHT) använder en snabb och robust algoritm för att segmentera kluster av ungefär samma plana sampel och avger röster för individuella kluster (istället för individuella sampel) på en ( θ , ) sfärisk ackumulator som använder en trivariat Gausskärna. Tillvägagångssättet är flera storleksordningar snabbare än befintliga (icke-deterministiska) tekniker för plandetektering i punktmoln, såsom RHT och RANSAC , och skalas bättre med storleken på datamängderna. Den kan användas med alla applikationer som kräver snabb detektering av plana funktioner på stora datamängder.
Hough transformation av kurvor, och dess generalisering för analytiska och icke-analytiska former
Även om versionen av transformationen som beskrivs ovan endast gäller för att hitta raka linjer, kan en liknande transform användas för att hitta vilken form som helst som kan representeras av en uppsättning parametrar. En cirkel, till exempel, kan omvandlas till en uppsättning av tre parametrar, som representerar dess centrum och radie, så att Hough-utrymmet blir tredimensionellt. Godtyckliga ellipser och kurvor kan också hittas på detta sätt, liksom vilken form som helst som lätt kan uttryckas som en uppsättning parametrar.
Generaliseringen av Hough-transformen för att detektera analytiska former i utrymmen som har någon dimensionalitet föreslogs av Fernandes och Oliveira. Till skillnad från andra Hough-transformationsbaserade tillvägagångssätt för analytiska former, beror Fernandes teknik inte på den form man vill upptäcka eller på indatatypen. Detekteringen kan drivas till en typ av analytisk form genom att ändra den antagna geometrimodellen där data har kodats (t.ex. euklidiskt utrymme , projektivt utrymme , konform geometri , och så vidare), medan den föreslagna formuleringen förblir oförändrad. Det garanterar också att de avsedda formerna representeras med minsta möjliga antal parametrar, och det tillåter samtidig detektering av olika typer av former som bäst passar en ingångsuppsättning poster med olika dimensioner och olika geometriska definitioner (t.ex. av plan och sfärer som bäst passar en uppsättning punkter, raka linjer och cirklar).
För mer komplicerade former i planet (dvs. former som inte kan representeras analytiskt i något 2D-rum) används Generalized Hough-transformen , som gör att en funktion kan rösta för en viss position, orientering och/eller skalning av formen med hjälp av en fördefinierad uppslagstabell. Hough-transformen ackumulerar bidrag från alla pixlar i den detekterade kanten.
Cirkeldetekteringsprocess
Att ändra algoritmen för att upptäcka cirkulära former istället för linjer är relativt enkelt.
- Först skapar vi ackumulatorutrymmet, som består av en cell för varje pixel. Initialt är varje cell satt till 0.
- För varje kantpunkt (i, j) i bilden, inkrementera alla celler som enligt ekvationen för en cirkel ( kan vara mitten av en cirkel. Dessa celler representeras av bokstaven i ekvationen.
- För varje möjligt värde på som finns i föregående steg, hitta alla möjliga värden på som uppfyller ekvationen.
- Sök efter lokala maxima i ackumulatorutrymmet. Dessa celler representerar cirklar som detekterades av algoritmen.
Om vi inte vet radien för cirkeln vi försöker lokalisera i förväg, kan vi använda ett tredimensionellt ackumulatorutrymme för att söka efter cirklar med en godtycklig radie. Naturligtvis är detta beräkningsmässigt dyrare.
Den här metoden kan också upptäcka cirklar som är delvis utanför ackumulatorutrymmet, så länge som tillräckligt med av cirkelns yta fortfarande finns inom den.
Detektering av 3D-objekt (plan och cylindrar)
Hough-transform kan också användas för att detektera 3D-objekt i avståndsdata eller 3D- punktmoln . Utvidgningen av klassisk Hough-transform för plandetektering är ganska enkel. Ett plan representeras av dess explicita ekvation för vilken vi kan använda ett 3D Hough-utrymme som motsvarar , och . Denna förlängning lider av samma problem som sin 2D-motsvarighet, dvs. nära horisontella plan kan detekteras på ett tillförlitligt sätt, medan prestandan försämras när plan riktning blir vertikal (stora värden på en x {\displaystyle a_{x} y förstärker bruset i data). Denna formulering av planet har använts för att detektera plan i punktmolnen som erhållits från luftburen laserskanning och fungerar mycket bra eftersom i den domänen alla plan är nästan horisontella.
För generaliserad plandetektering med hjälp av Hough-transform, kan planet parametriseras med sin normalvektor (med sfäriska koordinater) och dess avstånd från origo vilket resulterar i ett tredimensionellt Hough-utrymme. Detta resulterar i att varje punkt i ingångsdatan röstar för en sinusformad yta i Hough-utrymmet. Skärningen mellan dessa sinusformade ytor indikerar närvaron av ett plan. Ett mer allmänt tillvägagångssätt för mer än 3 dimensioner kräver att sökheuristik förblir genomförbar.
Hough-transform har också använts för att hitta cylindriska objekt i punktmoln med en tvåstegsmetod. Det första steget hittar cylinderns orientering och det andra steget hittar positionen och radien.
Använder viktade funktioner
En vanlig variationsdetalj. Det vill säga att hitta lagerplatserna med det högsta antalet i ett steg kan användas för att begränsa intervallet av värden som söks i nästa.
Noggrant valt parameterutrymme
Ett högdimensionellt parameterutrymme för Hough-transformen är inte bara långsamt, men om det implementeras utan eftertanke kan det lätt överskrida det tillgängliga minnet. Även om programmeringsmiljön tillåter allokering av en array som är större än det tillgängliga minnesutrymmet genom virtuellt minne, kommer antalet sidbyten som krävs för detta att vara mycket krävande eftersom ackumulator-arrayen används på ett slumpmässigt sätt och sällan stannar i angränsande minne eftersom den hoppar från index till index.
Överväg uppgiften att hitta ellipser i en 800x600 bild. Om man antar att radierna för ellipserna är orienterade längs huvudaxlarna, är parameterutrymmet fyrdimensionellt. ( x , y ) definierar mitten av ellipsen, och a och b anger de två radierna. Genom att tillåta mitten att vara var som helst i bilden, läggs begränsningen till 0<x<800 och 0<y<600. Om radierna ges samma värden som begränsningar är det som återstår en glest fylld ackumulatormatris med mer än 230 miljarder värden.
Det är osannolikt att ett sålunda utformat program tillåts allokera tillräckligt med minne. Detta betyder inte att problemet inte kan lösas, utan bara att nya sätt att begränsa storleken på ackumulatormatrisen ska hittas, vilket gör det möjligt. Till exempel:
- Om det är rimligt att anta att var och en av ellipserna finns helt och hållet i bilden, kan radiernas omfång reduceras. De största radierna kan vara är om mitten av ellipsen är i mitten av bilden, vilket gör att kanterna på ellipsen sträcker sig till kanterna. I detta extrema fall kan radierna endast vara halva storleken på bildstorleken orienterade i samma riktning. Att minska intervallet för a och b på detta sätt minskar ackumulatoruppsättningen till 57 miljarder värden.
- Byt noggrannhet mot utrymme i uppskattningen av mitten: Om centrum förutsägs vara avstängt med 3 på både x- och y-axeln minskar detta storleken på ackumulatormatrisen till cirka 6 miljarder värden.
- Byt noggrannhet för utrymme i uppskattningen av radierna: Om radierna uppskattas vara avstängda med 5 sker ytterligare minskning av storleken på ackumulatoruppsättningen, med cirka 256 miljoner värden.
- Beskär bilden till områden av intresse. Detta är bildberoende och därför oförutsägbart, men föreställ dig ett fall där alla kanter av intresse i en bild finns i den övre vänstra kvadranten av den bilden. Ackumulatormatrisen kan reduceras ytterligare i detta fall genom att begränsa alla fyra parametrarna med en faktor 2, för en total reduktionsfaktor på 16.
Genom att bara tillämpa de tre första av dessa begränsningar på exemplet som nämns om, reduceras storleken på ackumulatormatrisen med nästan en faktor 1000, vilket ger den ner till en storlek som är mycket mer sannolikt att passa i en modern dators minne.
Effektiv ellipsdetekteringsalgoritm
Yonghong Xie och Qiang Ji ger ett effektivt sätt att implementera Hough-transformen för ellipsdetektering genom att övervinna minnesproblemen. Som diskuteras i algoritmen (på sidan 2 i artikeln), använder detta tillvägagångssätt endast en endimensionell ackumulator (för den mindre axeln) för att upptäcka ellipser i bilden. Komplexiteten är O(N 3 ) i antalet punkter som inte är noll i bilden.
Begränsningar
Hough-transformeringen är bara effektiv om ett högt antal röster faller i den högra papperskorgen, så att papperskorgen lätt kan upptäckas bland bakgrundsljudet. Det betyder att soptunnan inte får vara för liten, annars faller en del röster i grannkorgen, vilket minskar synligheten för huvudkorgen.
Dessutom, när antalet parametrar är stort (det vill säga när vi använder Hough-transformen med vanligtvis fler än tre parametrar), är det genomsnittliga antalet röster som avgivits i en enstaka låda mycket lågt, och dessa lådor motsvarar en verklig siffra på bilden verkar inte nödvändigtvis ha ett mycket högre antal röster än sina grannar. Komplexiteten ökar med en hastighet av med varje ytterligare parameter, där är storleken på bildutrymmet och är antalet parametrar. (Shapiro och Stockman, 310) Således måste Hough-transformen användas med stor försiktighet för att upptäcka allt annat än linjer eller cirklar.
Slutligen är mycket av effektiviteten hos Hough-transformen beroende av kvaliteten på indata: kanterna måste detekteras väl för att Hough-transformen ska vara effektiv. Användning av Hough-transformen på brusiga bilder är en mycket känslig sak och generellt sett måste ett brussteg användas innan. I de fall då bilden är skadad av fläckar, vilket är fallet i radarbilder, föredras ibland Radontransformen för att detektera linjer, eftersom den dämpar bruset genom summering.
Se även
externa länkar
- hough_transform.cpp – C++-kod – exempel på CImg-bibliotek ( öppet källkodsbibliotek , C++- källkod, gråskalebilder )
- Interaktiv demonstration om grunderna i Hough Transform
- https://web.archive.org/web/20070827233423/http://www.rob.cs.tu-bs.de/content/04-teaching/06-interactive/Hough.html – Java-applet + källa för lärande Hough-transformationen i form av lutningsavskärning
- https://web.archive.org/web/20070827191440/http://www.rob.cs.tu-bs.de/content/04-teaching/06-interactive/HNF.html – Java-applet + källa för lärande Hough-transformationen i normal form
- http://www.sydlogan.com/deskew.html – Skruva bort bilder med Hough-transform ( gråskalabilder , C++- källkod)
- https://web.archive.org/web/20070922090216/http://imaging.gmse.net/articledeskew.html – Avskeda bilder med hjälp av Hough transform ( Källkod för Visual Basic )
- http://www.mitov.com/products/visionlab – Delphi , C++ och .NET gratis för utbildningsändamål bibliotek som innehåller Line, Circle och Line segment Hough transform-komponenter.
- Tarsha-Kurdi, F., Landes, T., Grussenmeyer, P., 2007a. Hough-transformera och utökade RANSAC-algoritmer för automatisk detektering av 3d-byggnadstakplan från Lidar-data. ISPRS-förfarande. Verkstad Laserskanning. Esbo, Finland, 12–14 september 2007.
- Into innehåller öppen källkod-implementationer av linjär och cirkulär Hough-transform i C++
- http://www.vision.ime.usp.br/~edelgado/defesa/code/hough.html Hough-transform för Ellipsdetektering, implementerad i C .
- scikit-image Hough-transform för linje, cirkel och ellips, implementerad i Python .
- [1] Hough-transform baserad på wavelet-filtrering, för att detektera en cirkel med en viss radie. ( Matlab- kod.)
- Hough transform för linjer med MATLAB
- Hough transform för cirklar i MATLAB
- KHT – C++ källkod.
- 3DKHT – C++ källkod och datauppsättningar.