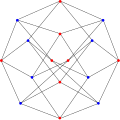
Hoffman graf

Hoffman-grafen
Hoffman-grafen
	Hoffman-grafen
Döpt efter	Alan Hoffman
Vertices	16
Kanter	32
Radie	3
Diameter	4
Omkrets	4
Automorfismer	48 ( Z /2 Z × S 4 )
Kromatiskt nummer	2
Kromatiskt index	4
Boktjocklek	3
Könummer	2
Egenskaper	; ; ; Hamiltonsk tvådelad Perfekt Eulerian
	Tabell över grafer och parametrar

Inom det matematiska området grafteorin är Hoffman -grafen en 4- regelbunden graf med 16 hörn och 32 kanter upptäckt av Alan Hoffman . Publicerad 1963, den är kospektral till hyperkubgrafen Q ₄ .

Hoffman-grafen har många gemensamma egenskaper med hyperkuben Q ₄ — båda är Hamiltonska och har kromatiskt nummer 2, kromatiskt index 4, omkrets 4 och diameter 4. Det är också en graf med 4 vertex och en 4 -kantsbunden graf . Den är dock inte avståndsregelbunden . Den har boktjocklek 3 och kö nummer 2.

Algebraiska egenskaper

Hoffman-grafen är inte en vertextransitiv graf och dess _{fullständiga} automorfismgrupp är en grupp av ordningen 48 isomorf till den direkta produkten av den symmetriska gruppen S4 och den cykliska gruppen Z / 2Z .

Det karakteristiska polynomet i Hoffman-grafen är lika med

(x-4)(x-2)^{4}x^{6}(x+2 )^{4}(x+4)

gör det till en integralgraf — en graf vars spektrum helt består av heltal. Det är samma spektrum som hyperkuben Q ₄ .