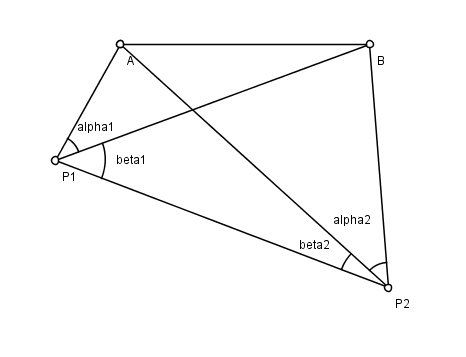
Hansens problem

Hansens problem är ett problem vid planmätning , uppkallad efter astronomen Peter Andreas Hansen (1795–1874), som arbetade med den geodetiska undersökningen av Danmark. Det finns två kända punkter A och B och två okända punkter P ₁ och P ₂ . Från P ₁ och P ₂ mäter en observatör vinklarna som görs av siktlinjerna till var och en av de andra tre punkterna. Problemet är att hitta positionerna för P ₁ och P ₂ . Se figur; de uppmätta vinklarna är ( α ₁ , β ₁ , α ₂ , β ₂ ).

Eftersom det handlar om observationer av vinklar gjorda vid okända punkter, är problemet ett exempel på resektion (i motsats till skärningspunkt).

Lösningsmetod översikt

Definiera följande vinklar: γ = P ₁ AP ₂ , δ = P ₁ BP ₂ , φ = P ₂ AB , ψ = P ₁ BA . Som ett första steg kommer vi att lösa för φ och ψ . Summan av dessa två okända vinklar är lika med summan av β ₁ och β ₂ , vilket ger ekvationen

\phi +\psi =\beta _{1}+\beta _{2}.

En andra ekvation kan hittas mer mödosamt, enligt följande. Sinuslagen ger efter

{\frac {AB}{P_{2}B}}={\frac {\sin \alpha _{2}}{\sin \phi } }

och

{\frac {P_{2}B}{P_{1}P_{2}}}={\frac {\sin \beta _{1}}{\sin \delta }}.

Genom att kombinera dessa får vi

{\frac {AB}{P_{1}P_{2}}}={\frac {\sin \alpha _{2}\sin \beta _{1}}{\sin \phi \sin \ delta }}.

Helt analoga resonemang på andra sidan ger

{\frac {AB}{P_{1}P_{2}}}={\frac {\sin \alpha _{1}\sin \beta _{2}}{\sin \psi \sin \ gamma }}.

Att sätta dessa två lika ger

{\frac {\sin \phi }{\sin \psi }}={\frac {\sin \gamma \sin \alpha _{2}\sin \beta _{1}}{\sin \delta \sin \alpha _{1}\sin \beta _{2}}}=k.

Med en känd trigonometrisk identitet kan detta sinusförhållande uttryckas som tangenten för en vinkelskillnad:

\tan {\frac {\phi -\psi }{2}}={\frac {k-1}{k+1}}\tan {\frac {\phi +\psi }{2}} .

Där ${k=}{\frac {\sin \phi }{\sin \psi }}.$

Det här är den andra ekvationen vi behöver. När vi löst de två ekvationerna för de två okända $\phi$ och $\psi$ , kan vi använda något av de två uttrycken ovan för ${\frac {AB }{P_{1}P_{2}}}$ för att hitta P ₁ P ₂ eftersom AB är känt. Vi kan sedan hitta alla andra segment med hjälp av sinuslagen.

Lösningsalgoritm

Vi får fyra vinklar ( α ₁ , β ₁ , α ₂ , β ₂ ) och avståndet AB . Beräkningen går till enligt följande:

Beräkna $\gamma =\pi -\alpha _{1}-\beta _{1}-\beta _{2},\quad \delta =\pi -\alpha _{2}-\beta _{1 }-\beta _{2}.$
Beräkna $k={\frac {\sin \gamma \sin \alpha _{2}\sin \beta _{1}}{\sin \delta \sin \alpha _{1}\sin \beta _{2 }}}.$
Låt ${\displaystyle s=\beta _{1}+\beta _{2},\quad d=2\arctan \left[{\frac {k-1}{k+1}}\tan(s/2)\right]} och$ sedan $\phi =(s+d)/2,\quad \psi =(sd)/2.$
Beräkna $P_{1}P_{2}=AB{\frac {\sin \phi \sin \delta }{\sin \alpha _{2}\sin \beta _{1}}}$ eller motsvarande $P_{1}P_{2}=AB{\frac {\sin \psi \sin \gamma }{\sin \alpha _{1}\sin \beta _{2}}}.$ Om ett av dessa bråk har en nämnare nära noll, använd den andra.

Se även