Gradientnätverk

Inom nätverksvetenskap är ett gradientnätverk ett riktat delnätverk av ett oriktat "substrat" -nätverk där varje nod har en associerad skalär potential och en utlänk som pekar på noden med den minsta (eller största) potentialen i dess grannskap, definierad som föreningen av sig själv och dess grannar på substratnätverket.

Definition

Transport sker på ett fast nätverk $G=G(V,E)$ som kallas substratgrafen. Den har N noder, $V=\{0,1,...,N-1\}$ och uppsättningen kanter $E=\{(i,j)|i,j\in V\}$ . Givet en nod i , kan vi definiera dess uppsättning grannar i G med S _i ⁽¹⁾ = {j ∈ V | (i,j)∈ E}.

Ett exempel på ett gradientnätverk.

₀ Låt oss också betrakta ett skalärt fält, h = { h , .., h _{N −1} } definierat på uppsättningen av noder V, så att varje nod i har ett skalärt värde h _i associerat till sig.

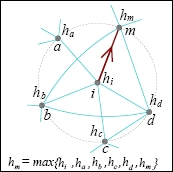
Gradient ∇ h _i på ett nätverk : ∇h _i $=$ (i, μ(i)) dvs den riktade kanten från i till μ(i) , där μ ( i ) ∈ S _i ⁽¹⁾ ∪ { i}, och h _μ har det maximala värdet i ${h_{j}|j\in S_{i}^{(1)}\cup {i}}$ .

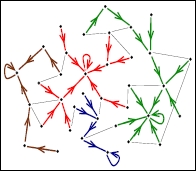
Gradientnätverk : ∇ $G=$ ∇ $G$$(V,F)$ där F är uppsättningen av gradientkanter på G .

I allmänhet beror det skalära fältet på tid, på grund av flödet, externa källor och sänkor på nätverket. Därför kommer gradientnätverket ∇ $G$ att vara dynamiskt.

Motivation och historia

Konceptet med ett gradientnätverk introducerades först av Toroczkai och Bassler (2004).

I allmänhet är verkliga nätverk (som citationsdiagram , Internet , cellulära metaboliska nätverk, det världsomspännande flygplatsnätverket), som ofta utvecklas till transportenheter som information, bilar, kraft, vatten, styrkor och så vidare, inte globala designad; istället utvecklas och växer de genom lokala förändringar. Till exempel, om en router på Internet ofta är överbelastad och paket går förlorade eller försenas på grund av det, kommer den att ersättas av flera sammankopplade nya routrar.

Dessutom genereras eller påverkas ofta detta flöde av lokala gradienter i en skalär. Till exempel: elektrisk ström drivs av en gradient av elektrisk potential. I informationsnätverk kommer egenskaperna hos noderna att generera en förspänning i hur information överförs från en nod till dess grannar. Denna idé motiverade tillvägagångssättet att studera ett nätverks flödeseffektivitet genom att använda gradientnätverk, när flödet drivs av gradienter av ett skalärt fält distribuerat på nätverket.

Senare forskning undersöker sambandet mellan nätverkstopologi och transportens flödeseffektivitet.

Gradienten vid nod i är en riktad kant som pekar mot den största ökningen av den skalära potentialen i nodens grannskap.

Gradientdistribution av gradientnätverk

I ett gradientnätverk är in-graden för en nod i, k _i ⁽ⁱⁿ⁾ antalet gradientkanter som pekar in i i, och in-grad-fördelningen är $R(l)=P\{k_{i}^{(in)}=l\}$ .

Gradientfördelningarna för gradientnätverket och substratet ( BA Model) .

När substratet G är en slumpmässig graf och varje nodpar är kopplat till sannolikheten P (dvs. en Erdős–Rényi slumpmässig graf ), är skalärerna h _i iid (oberoende identiskt fördelade) det exakta uttrycket för R(l) ges av

${\ displaystyle R(l)={\frac {1}{N}}\summa _{n=0}^{N-1}\mathrm {C} _{l}^{N-1-n}[1- p(1-p)]^{N-1-nl}[p(1-p)^{n}]^{l}]}$

I gränsen $N\to \infty$ och $P\to 0$ blir gradfördelningen maktlagen

$R(l)\approx l^{-1}$

Detta visar i denna gräns, gradientnätverket för slumpmässiga nätverk är skalfritt.

Dessutom, om substratnätverket G är skalfritt, som i Barabási–Albert-modellen , följer gradientnätverket också maktlagen med samma exponent som G.

Trängseln på näten

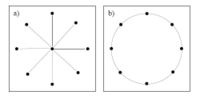
Det faktum att topologin för substratnätverket påverkar nivån av nätverksstockning kan illustreras med ett enkelt exempel: om nätverket har en stjärnliknande struktur, då vid den centrala noden, skulle flödet bli överbelastat eftersom den centrala noden ska hantera allt flöde från andra noder. Men om nätverket har en ringliknande struktur, eftersom varje nod tar samma roll, finns det ingen flödesstockning.

Illustrerar strukturens inverkan på flöden.

Under antagande att flödet genereras av gradienter i nätverket, kan flödeseffektiviteten på nätverk karakteriseras genom störningsfaktorn (eller överbelastningsfaktorn), definierad enligt följande:

$J=1-\langle \langle {\frac {N_{\text{receive}}}{N_{\text{send} }}}\rangle _{h}\rangle _{\text{nätverk}}=R(0)$

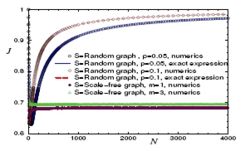
där N _motta är antalet noder som tar emot gradientflöde och N _skicka är antalet noder som skickar gradientflöde. Värdet på J är mellan 0 och 1; $J=0$ betyder ingen trängsel, och $J=1$ motsvarar maximal trängsel. I gränsen $N\to \infty$ , för en Erdős–Rényi slumpmässig graf , blir överbelastningsfaktorn

$J(N,P)=1-{\frac {\ ln N}{N\ln({\frac {1}{1-P}})}}\vänster[1+O({\frac {1}{N}})\höger]\högerpil 1.$

Detta resultat visar att slumpmässiga nätverk är maximalt överbelastade inom den gränsen. Tvärtom, för ett skalfritt nätverk J en konstant för vilket N som helst , vilket betyder att skalfria nätverk inte är benägna att störa maximalt.

Fig. 7. Överbelastningskoefficienten för slumpmässiga grafer och skalfria nätverk.

Tillvägagångssätt för att kontrollera trängseln

Ett problem i kommunikationsnätverk är att förstå hur man kontrollerar trafikstockningar och upprätthåller normal och effektiv nätverksfunktion.

Zonghua Liu et al. (2006) visade att det är mer sannolikt att överbelastning uppstår vid noderna med höga grader i nätverk, och ett effektivt tillvägagångssätt för att selektivt förbättra meddelandeprocesskapaciteten hos en liten del (t.ex. 3 %) av noderna har visat sig fungera lika bra som förbättrar kapaciteten hos alla noder.

Ana L Pastore och Piontti et al. (2008) visade att avslappningsdynamik kan minska nätstockning.

Pan et al. (2011) studerade störningsegenskaper i ett schema där kanter ges vikter av en potens av den skalära skillnaden mellan nodpotentialer.

Niu och Pan (2016) visade att överbelastning kan minskas genom att införa en korrelation mellan gradientfältet och den lokala nätverkstopologin.

<n(k)>är det genomsnittliga paketnumret som en funktion av grad, paketbearbetningsförmåga: 0 (cirklar), 0,05 (kvadrater), 0,1 (stjärnor).

Jämförelsen mellan det effektiva tillvägagångssättet (cirklar) med kapaciteten hos topp 3 % graders noder förbättrad och den normala ansatsen (stjärnor) med kapaciteten hos alla noder förbättrad. (a) paketbearbetningsförmåga är lika med 0,05, (b) paketbearbetningsförmåga är lika med 0,1. är det genomsnittliga paketnumret som en funktion av graden.

Se även

• Nätverksdynamik
• Nätverks topologi
• Kvantkomplexa nätverk