Formfaktor (elektronik)

Inom elektronik eller elektroteknik är formfaktorn för en växelströmsvågform (signal) förhållandet mellan RMS- värdet ( root mean square ) och medelvärdet (matematiskt medelvärde av absoluta värden för alla punkter på vågformen). Den identifierar förhållandet mellan likströmmen med lika effekt i förhållande till den givna växelströmmen. Den förra kan också definieras som den likström som kommer att producera ekvivalent värme.

Beräknar formfaktorn

För en idealisk, kontinuerlig vågfunktion över tiden T, kan RMS beräknas i integralform :

$X_{\mathrm {rms} }={\sqrt {{1 \över {T}}{\int _{ t_{0}}^{t_{0}+T}{[x(t)]}^{2}\,dt}}}$

Det korrigerade medelvärdet är då medelvärdet av integralen av funktionens absoluta värde:

$X_{\mathrm {arv} }={1 \över {T}}{\int _{t_{0}}^{t_{0}+T}{|x(t)|\, dt}}$

Kvoten för dessa två värden är formfaktorn, ${\displaystyle k_{\mathrm {f} }} , eller$ i entydiga situationer, $k$ .

$k_{\mathrm {f} }={\frac {\mathrm {RMS} }{\mathrm {ARV} }}={\frac {\sqrt {{1 \over {T}}{\ int _{t_{0}}^{t_{0}+T}{[x(t)]}^{2}\,dt}}}{{1 \över {T}}{\int _{t_ {0}}^{t_{0}+T}{|x(t)|\,dt}}}}={\frac {\sqrt {T\int _{t_{0}}^{t_{0 }+T}{{[x(t)]}^{2}\,dt}}}{\int _{t_{0}}^{t_{0}+T}{|x(t)|\ ,dt}}}$

$X_{\mathrm {rms} }$ speglar variationen i funktionens avstånd från medelvärdet och påverkas oproportionerligt mycket av stora avvikelser från det okorrigerade medelvärdet. Den kommer alltid att vara minst lika stor som ${\displaystyle X_{\mathrm {arv} }} ,$ vilket bara mäter det absoluta avståndet från nämnda medelvärde. Formfaktorn kan alltså inte vara mindre än 1 (en fyrkantsvåg där alla momentana värden ligger lika långt över eller under medelvärdet; se nedan), och har ingen teoretisk övre gräns för funktioner med tillräcklig avvikelse.

$\mathrm {RMS} _{\mathrm {total} }={\sqrt {{{\mathrm {RMS} _{1}}^{2}}+{{\mathrm { RMS} _{2}}^{2}}+...+{{\mathrm {RMS} _{n}}^{2}}}}$

kan användas för att kombinera signaler med olika frekvenser (till exempel för övertoner), medan för samma frekvens, $\mathrm {RMS} _{\mathrm {total} }=\mathrm {RMS} _{1}+\mathrm {RMS} _{2}+...+\mathrm {RMS } _{n}$ .

Eftersom ARVs på samma domän kan summeras $\mathrm {ARV} _{\mathrm {total} }=\mathrm {ARV} _{1}+\mathrm {ARV} _{2}+...+\mathrm {ARV } _{n}$ , formfaktorn för en komplex våg som består av flera vågor med samma frekvens kan ibland beräknas som

$k_{\mathrm {f} _{\mathrm {tot} }}={\frac {\mathrm {RMS} _{\mathrm {tot} }}{\mathrm {ARV} _ {\mathrm {tot} }}}={\frac {\mathrm {RMS} _{1}+...+\mathrm {RMS} _{n}}{\mathrm {ARV} _{1}+. ..+\mathrm {ARV} _{n}}}$ .

Ansökan

AC-mätinstrument är ofta byggda med specifika vågformer i åtanke. Till exempel är många multimetrar i deras AC-områden specifikt skalade för att visa RMS-värdet för en sinusvåg. Eftersom RMS-beräkningen kan vara svår att uppnå digitalt, beräknas istället det absoluta medelvärdet och resultatet multipliceras med formfaktorn för en sinusform. Denna metod ger mindre exakta avläsningar för andra vågformer än en sinusvåg, och instruktionsskylten på baksidan av en Avometer anger detta uttryckligen.

Kvadreringen i RMS och det absoluta värdet i ARV gör att både värdena och formfaktorn är oberoende av vågfunktionens tecken (och därmed den elektriska signalens riktning) vid någon punkt. Av denna anledning är formfaktorn densamma för en riktningsskiftande våg med ett regelbundet medelvärde på 0 och dess helt korrigerade version.

Formfaktorn, $k_{\mathrm {f} }$ , är den minsta av de tre vågfaktorerna, de andra två är toppfaktorn ${\displaystyle k_{ \mathrm {a} }={\frac {X_{\mathrm {max} }}{X_{\mathrm {rms} }}}} och den mindre kända$ medelvärdesfaktorn $k_{\mathrm {av} }={\frac {X_{\mathrm {max} }}{X_{\mathrm {arv} }}}$ .

$k_{\mathrm {av} }\geq k_{\mathrm {a} }\geq k_{\mathrm {f} }$

På grund av deras definitioner (alla förlitar sig på Root Mean Square , Average likriktat värde och maximal amplitud för vågformen), är de tre faktorerna relaterade till $k_{\mathrm {av} }= k_{\mathrm {a} }k_{\mathrm {f} }$ , så formfaktorn kan beräknas med $k_{\mathrm {f} }={\frac { k_{\mathrm {av} }}{k_{\mathrm {a} }}}$ .

Specifika formfaktorer

$a$ representerar amplituden för funktionen och alla andra koefficienter som tillämpas i den vertikala dimensionen. Till exempel $8\sin(t)$ analyseras som $f(t)=a\sin( t),\ a=8$ . Eftersom både RMS och ARV är direkt proportionella mot det har det ingen effekt på formfaktorn och kan ersättas med en normaliserad 1 för att beräkna det värdet.

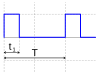
$D={\frac {\tau }{T}}$ är arbetscykeln , förhållandet mellan "puls"-tiden $\tau$ (när funktionens värde inte är noll) till hela vågperioden T $\displaystyle T}$ . De flesta grundläggande vågfunktioner uppnår bara 0 för oändligt korta ögonblick och kan därför anses ha $\tau =T,D=1$ , Men vilken som helst av de icke-pulserande funktionerna nedan kan läggas till med ${\frac {\sqrt {D}}{D}}={\frac {1}{\sqrt { D}}}={\sqrt {\frac {T}{\tau }}}$

för att tillåta pulsering. Detta illustreras med den halvlikriktade sinusvågen, som kan betraktas som en pulsad hellikriktad sinusvåg med ${\displaystyle D={\frac {1}{2}}} ,$ och har $k_{\mathrm {f} }=k_{\mathrm {f} _{\mathrm {frs} }}{\sqrt {2}}$ .

Vågform	Bild	RMS	ARV	Formfaktor
Sinusvåg		${\frac {a}{\sqrt {2}}}$	$a{\frac {2}{\pi }}$	${\frac {\pi }{2{\sqrt {2}}}}\approx 1.11072073$
Halvvågslikriktad sinus		${\frac {a}{2}}$	${\frac {a}{\pi }}$	${\frac {\pi }{2}}\approx 1.571$
Fullvågslikriktad sinus		${\frac {a}{\sqrt {2}}}$	$a{\frac {2}{\pi }}$	${\frac {\pi }{2{\sqrt {2}}}}$
Fyrkantsvåg , konstant värde		$a$	$a$	${\frac {a}{a}}=1$
Pulsvåg		$a{\sqrt {D}}$	$aD$	${\frac {1}{\sqrt {D}}}={\sqrt {\frac {T}{\tau }}}$
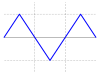
Triangelvåg		${\frac {a}{\sqrt {3}}}$	${\frac {a}{2}}$	${\frac {2}{\sqrt {3}}}\approx 1,15470054$
Sågtandsvåg		${\frac {a}{\sqrt {3}}}$	${\frac {a}{2}}$	${\frac {2}{\sqrt {3}}}$
Enhetligt slumpmässigt brus U (-a,a)		${\frac {a}{\sqrt {3}}}$	${\frac {a}{2}}$	${\frac {2}{\sqrt {3}}}$
Gaussiskt vitt brus G (σ)		$\sigma$	${\sqrt {\frac {2}{\pi }}}\sigma$	${\sqrt {\frac {\pi }{2}}}$