Aggregerad funktion

I databashantering är en aggregeringsfunktion eller aggregeringsfunktion en funktion där värdena för flera rader grupperas för att bilda ett enda sammanfattningsvärde .

(Figur 1) Entitetsrelationsdiagram representation av aggregering.

Vanliga aggregerade funktioner inkluderar:

Andra inkluderar:

Nanmean (menar att ignorera NaN-värden, även känd som "noll" eller "null")
Stddev

Formellt tar en aggregerad funktion som indata en uppsättning , en multiset (påse) eller en lista från någon indatadomän $I$ och matar ut ett element av en utdatadomän $O$ . Ingångs- och utdatadomänerna kan vara desamma, som för SUM , eller kan vara olika, till exempel för COUNT .

Aggregatfunktioner förekommer vanligtvis i många programmeringsspråk , i kalkylblad och i relationalgebra .

Listagg - funktionen, enligt definitionen i SQL:2016- standarden, samlar data från flera rader till en enda sammanlänkade sträng.

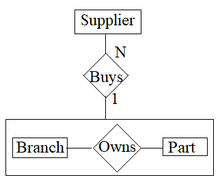
I entitetsrelationsdiagrammet representeras aggregering som ses i figur 1 med en rektangel runt relationen och dess enheter för att indikera att den behandlas som en aggregerad enhet.

Nedbrytbara aggregatfunktioner

Aggregatfunktioner utgör en flaskhals eftersom de potentiellt kräver att alla indatavärden finns på en gång. Vid distribuerad beräkning är det önskvärt att dela upp sådana beräkningar i mindre bitar och fördela arbetet, vanligtvis parallellt , via en divide and conquer-algoritm .

Vissa aggregatfunktioner kan beräknas genom att beräkna aggregatet för delmängder och sedan aggregera dessa aggregat; exempel inkluderar COUNT , MAX , MIN och SUM . I andra fall kan aggregatet beräknas genom att beräkna hjälpnummer för delmängder, aggregera dessa hjälptal och slutligen beräkna det totala numret i slutet; exempel inkluderar AVERAGE (spårningssumma och antal, dividering i slutet) och RANGE (spårning av max och min, subtrahering i slutet). I andra fall kan aggregatet inte beräknas utan att analysera hela uppsättningen på en gång, även om i vissa fall approximationer kan distribueras; exempel inkluderar DISTINCT COUNT , MEDIAN och MODE .

Sådana funktioner kallas nedbrytbara aggregeringsfunktioner eller nedbrytbara aggregerade funktioner . De enklaste kan hänvisas till som självupplösbara aggregeringsfunktioner , som definieras som de funktioner $f$ så att det finns en sammanfogningsoperator $\diamond$ så att

f(X\uplus Y)=f(X)\diamond f(Y)

där $\uplus$ är föreningen av multiset (se monoid homomorfism ).

Till exempel, SUM :

{\displaystyle \operatorname {SUM} ({x})=x} ,

för en singelton;

\operatörsnamn {SUM} (X\uplus Y)=\operatörsnamn {SUM} (X)+\operatörsnamn {SUM} (Y )

, vilket betyder att merge

\diamond

helt enkelt är addition.

COUNT :

\operatorname {COUNT} ({x})=1

,

\operatorname {COUNT } (X\uplus Y)=\operatörsnamn {COUNT} (X)+\operatörsnamn {COUNT} (Y)

.

MAX :

\operatorname {MAX} ({x})=x

,

\ operatörsnamn {MAX} (X\uplus Y)=\max {\bigl (}\operatörsnamn {MAX} (X),\operatörsnamn {MAX} (Y){\bigr )}

.

MIN :

{\textstyle \operatorname {MIN} ({x})=x}

,

\ operatörsnamn {MIN} (X\uplus Y)=\min {\bigl (}\operatörsnamn {MIN} (X),\operatörsnamn {MIN} (Y){\bigr )}

.

Observera att självupplösbara aggregeringsfunktioner kan kombineras (formellt tar produkten) genom att tillämpa dem separat, så att man till exempel kan beräkna både SUMMA och COUNT samtidigt genom att spåra två tal.

Mer generellt kan man definiera en nedbrytbar aggregeringsfunktion $f som$ $f=g\circ h,f(X)=g(h(X))$ som kan uttryckas som sammansättningen av en slutlig funktion $g$ och en självupplösbar aggregeringsfunktion $h ,$ . Till exempel, AVERAGE = SUM / COUNT och RANGE = MAX − MIN .

I MapReduce- ramverket är dessa steg kända som InitialReduce (värde på enskild post/singleton-uppsättning), Combine (binär sammanslagning på två aggregationer) och FinalReduce (slutlig funktion på hjälpvärden) och flyttande nedbrytbar aggregering innan Shuffle-fasen är känd som ett InitialReduce-steg,

Nedbrytbara aggregeringsfunktioner är viktiga i online analytisk bearbetning (OLAP), eftersom de tillåter att aggregeringsfrågor beräknas på de förberäknade resultaten i OLAP-kuben snarare än på basdata. Det är till exempel lätt att stödja COUNT , MAX , MIN och SUM i OLAP, eftersom dessa kan beräknas för varje cell i OLAP-kuben och sedan sammanfattas ("rullas upp"), men det är svårt att stödja MEDIAN , eftersom som måste beräknas för varje vy separat.

Andra nedbrytbara aggregatfunktioner

För att beräkna medelvärdet och standardavvikelsen från aggregerade data är det nödvändigt att ha tillgängligt för varje grupp: summan av värden (Σx _i = SUM(x)), antalet värden (N=COUNT(x)) och summan av kvadrater av värdena (Σx _i² =SUM(x ² )) för varje grupp. AVG :