Faber–Jackson relation

Hastighetsspridning ( y -axel) plottad mot absolut magnitud ( x -axel) för ett prov av elliptiska galaxer , med Faber-Jackson-relationen visad i blått.

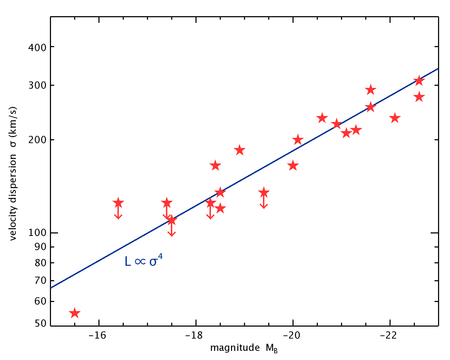
Relationen Faber–Jackson gav den första empiriska maktlagsrelationen mellan ljusstyrkan $L$ och den centrala stjärnhastighetsspridningen $\sigma }$ displaystyle i den elliptiska galaxen , och presenterades av astronomerna Sandra M. Faber och Robert Earl Jackson 1976. Deras relation kan uttryckas matematiskt som:

$L\propto \sigma ^{\gamma }$

med indexet $\gamma$ ungefär lika med 4.

År 1962 hade Rudolph Minkowski upptäckt och skrev att en "korrelation mellan hastighetsspridning och [luminositet] existerar, men den är dålig" och att "det verkar viktigt att utöka observationerna till fler objekt, särskilt vid låga och medelstora absoluta magnituder". Detta var viktigt eftersom värdet på $\gamma$ beror på omfånget av galaxens ljusstyrka som är anpassad, med ett värde på 2 för elliptiska galaxer med låg ljusstyrka upptäckt av ett team ledd av Roger Davies , och ett värde på 5 rapporterad av Paul L. Schechter för lysande elliptiska galaxer.

Relationen Faber–Jackson förstås som en projektion av elliptiska galaxers grundplan . En av dess huvudsakliga användningsområden är som ett verktyg för att bestämma avstånd till externa galaxer.

Teori

Gravitationspotentialen för en massfördelning med radien $R$ och massan $\displaystyle M}$ { ges av uttrycket:

$U=-\alpha {\frac {GM^{2}}{R}}$

Där α är en konstant beroende på t.ex. systemets densitetsprofil och G är gravitationskonstanten . För en konstant densitet, $\alpha \ ={\frac {3}{5}}$

Den kinetiska energin är:

$K={\frac {1}{2}}MV^{2}={\frac {3}{2}}M\sigma ^{2 }$

(Kom ihåg att $\sigma$ är den 1-dimensionella hastighetsspridningen. Därför är $3\sigma ^{2}=V^{2}$ .) Från virialsatsen ( $2K+U=0$ ) följer

$\sigma ^{2}={\frac {1}{5}}{\frac {GM}{R}}.$

Om vi ​​antar att förhållandet mellan massa och ljus, $M/L$ , är konstant, t.ex. $M\propto L$ kan vi använda detta och uttrycket ovan för att få en relation mellan $R$ och $\sigma ^{2}$ :

$R\propto {\frac {LG}{\sigma ^{2}}}.$

Låt oss introducera ytljusstyrkan, $B=L/(4\pi R^{2})$ och anta att detta är en konstant (vilket ur en fundamental teoretisk synvinkel , är ett helt omotiverat antagande) att få

$L=4\pi R^{2}B.$

Genom att använda detta och kombinera det med relationen mellan $R$ och $L$ , resulterar detta i

$L\propto 4\pi \left({\frac {LG}{\sigma ^{2}}}\right)^{2}B$

och genom att skriva om uttrycket ovan får vi slutligen förhållandet mellan ljusstyrka och hastighetsspridning:

$L\propto {\frac {\sigma ^{4}}{4\pi G^{2}B}},$

det är

$L\propto \sigma ^{4}.$

Med tanke på att massiva galaxer härrör från homolog sammansmältning, och de svagare från försvinnande, kan antagandet om konstant ytljusstyrka inte längre stödjas. Empiriskt uppvisar ytljusstyrkan en topp vid ungefär $M_{V}=-23$ . Den reviderade relationen blir då

$L\propto \sigma ^{3.1}$

för de mindre massiva galaxerna, och

$L\propto \sigma ^{15.0}$

för de mer massiva. Med dessa reviderade formler delas grundplanet i två plan som lutar cirka 11 grader mot varandra.

Inte ens förstarangerade galaxhopar har konstant ytljusstyrka. Ett påstående som stöder konstant ytljusstyrka presenterades av astronomen Allan R. Sandage 1972 baserat på tre logiska argument och hans egna empiriska data. 1975 visade Donald Gudehus att vart och ett av de logiska argumenten var felaktiga och att förstarangerade galaxkluster uppvisade en standardavvikelse på ungefär en halv magnitud.

Uppskattning av avstånd till galaxer

Liksom Tully-Fisher-relationen ger Faber-Jackson-relationen ett sätt att uppskatta avståndet till en galax, vilket annars är svårt att få, genom att relatera det till mer lätt observerbara egenskaper hos galaxen. I fallet med elliptiska galaxer, om man kan mäta den centrala stjärnhastighetsspridningen, vilket kan göras relativt enkelt genom att använda spektroskopi för att mäta dopplerförskjutningen av ljus som emitteras av stjärnorna, då kan man få en uppskattning av den verkliga ljusstyrkan hos galaxen via relationen Faber–Jackson. Detta kan jämföras med galaxens skenbara magnitud , som ger en uppskattning av avståndsmodulen och därmed avståndet till galaxen.

Genom att kombinera en galaxs centrala hastighetsspridning med mätningar av dess centrala ytljusstyrka och radieparameter är det möjligt att förbättra uppskattningen av galaxens avstånd ännu mer. Denna standardmåttstock, eller "reduced galaxian radius-parameter", $r_{g}$ , utarbetad av Gudehus 1991, kan ge avstånd, fria från systematisk förspänning, exakta till cirka 31%.

Se även

• Grundplan (elliptiska galaxer)
• M–sigma relation
• Sigma-D relation
• Tully-Fisher relation

externa länkar

• Originaltidningen av Faber & Jackson
• Gudehus revidering av förhållandet Faber–Jackson