Förvrängd krets

Förvrängd krets är ett kryptografiskt protokoll som möjliggör säker beräkning av två parter där två misstroende parter gemensamt kan utvärdera en funktion över sina privata ingångar utan närvaro av en pålitlig tredje part. I det förvanskade kretsprotokollet måste funktionen beskrivas som en boolesk krets .

Historien om förvrängda kretsar är komplicerad. Uppfinningen av den förvrängda kretsen krediterades Andrew Yao , eftersom Yao introducerade idén i den muntliga presentationen av ett papper i FOCS '86. Detta dokumenterades av Oded Goldreich 2003. Det första skriftliga dokumentet om denna teknik var av Goldreich, Micali och Wigderson i STOC '87. Termen "förvrängd krets" användes först av Beaver, Micali och Rogaway i STOC'90. Yaos protokoll för att lösa Yaos miljonärsproblem var det första exemplet på säker beräkning, men det är inte direkt relaterat till förvrängda kretsar.

Bakgrund

Omedveten överföring

I det förvrängda kretsprotokollet använder vi oss av oblivious transfer . I den omedvetna överföringen överförs en sträng mellan en avsändare och en mottagare på följande sätt: en avsändare har två strängar $S_{0}$ och $S_{1}$ . Mottagaren väljer $i\in \{0,1\}$ och avsändaren skickar $S_{i}$ med det oblivious transfer-protokollet så att

mottagaren får ingen information om den osända strängen $S_{(1-i)}$ ,
värdet av $i$ exponeras inte för avsändaren.

Observera att även om mottagaren inte känner till $S_{0},S_{1}$ -värdena, vet mottagaren i praktiken viss information om vad $S_{i}$ kodar så att mottagaren inte blint väljer $i$ . Det vill säga, om $S_{0}$ kodar ett falskt värde, $S_{1}$ kodar ett sant värde och mottagaren vill få det kodade sanna värdet, väljer mottagaren $i=1$ .

Den omedvetna överföringen kan byggas med asymmetrisk kryptografi som RSA-kryptosystemet .

Definitioner och notationer

Operator $\parallel$ är strängsammansättning . Operator $\oplus$ är bitvis XOR . k är en säkerhetsparameter och längden på nycklar. Den bör vara större än 80 och är vanligtvis inställd på 128.

Förvanskat kretsprotokoll

Protokollet består av 6 steg enligt följande:

Den underliggande funktionen (t.ex. i miljonärernas problem, jämförelsefunktion) beskrivs som en boolesk krets med 2-ingångsgrindar. Kretsen är känd för båda parter. Detta steg kan göras i förväg av en tredje part.
Alice förvanskar (krypterar) kretsen. Vi kallar Alice för garbler .
Alice skickar den förvrängda kretsen till Bob tillsammans med hennes krypterade indata.
För att kunna beräkna kretsen måste Bob också förvanska sin egen inmatning. För detta ändamål behöver han Alice för att hjälpa honom, eftersom bara garbler vet hur man krypterar. Slutligen kan Bob kryptera sin input genom omedveten överföring. När det gäller definitionen från ovan är Bob mottagaren och Alice avsändaren vid denna omedvetna överföring.
Bob utvärderar (dekrypterar) kretsen och erhåller de krypterade utdata. Vi kallar Bob för utvärderaren .
Alice och Bob kommunicerar för att lära sig resultatet.

Kretsgenerering

Den booleska kretsen för små funktioner kan genereras för hand. Det är konventionellt att göra kretsen av 2-ingångs XOR- och AND -grindar . Det är viktigt att den genererade kretsen har det minsta antalet OCH-grindar (se Gratis XOR-optimering ) . Det finns metoder som genererar den optimerade kretsen i termer av antalet OCH-grindar med hjälp av logisk syntesteknik . Kretsen för miljonärsproblemet är en digital komparatorkrets (som är en kedja av hela adderare som arbetar som en subtraktor och matar ut bärflaggan ). En komplett adderare kan implementeras med endast en AND- grind och vissa XOR- grindar. Detta betyder att det totala antalet OCH-grindar för kretsen för miljonärsproblemet är lika med bitbredden på ingångarna.

Förvirring

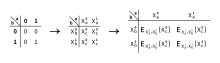
Ledningar och deras etiketter vid en OCH-grind

Konstruktion av sanningstabellen för en OCH-grind

Alice (garbler) krypterar den booleska kretsen i detta steg för att få en förvrängd krets . Alice tilldelar två slumpmässigt genererade strängar som kallas etiketter till varje tråd i kretsen: en för boolesk semantisk 0 och en för 1. (Etiketten är k-bit lång där k säkerhetsparametern och är vanligtvis inställd på 128.) Därefter går hon till alla grindar i kretsen och ersätter 0 och 1 i sanningstabellerna med motsvarande etiketter. Tabellen nedan visar sanningstabellen för en OCH-grind med två ingångar $w^{a},w^{b}$ och utgång $w^{c}$ :

a	b	c
0	0	0
0	1	0
1	0	0
1	1	1

Alice ersatte 0 och 1 med motsvarande etiketter:

a	b	c
$X_{0}^{a}$	$X_{0}^{b}$	$X_{0}^{c}$
$X_{0}^{a}$	$X_{1}^{b}$	$X_{0}^{c}$
$X_{1}^{a}$	$X_{0}^{b}$	$X_{0}^{c}$
$X_{1}^{a}$	$X_{1}^{b}$	$X_{1}^{c}$

Hon krypterar sedan utdataposten från sanningstabellen med motsvarande två inmatningsetiketter. Den krypterade tabellen kallas förvanskad tabell. Detta görs så att man bara kan dekryptera den förvanskade tabellen om han har de rätta två inmatningsetiketterna. I tabellen nedan $Enc_{k}(X)$ en dubbelnyckelsymmetrisk kryptering där k är den hemliga nyckeln och X är värdet som ska krypteras (se Fixed-Key Blockchiffer ).

Förvrängd tabell
$Enc_{X_{0}^{a},X_{0}^{b}}(X_{0}^{c})$
$Enc_{X_{0}^{a},X_{1}^{b}}(X_{0}^{c})$
$Enc_{X_{1}^{a},X_{0}^{b}}(X_{0}^{c})$
$Enc_{X_{1}^{a},X_{1}^{b}}(X_{1}^{c})$

Efter detta permuterar Alice slumpmässigt tabellen så att utdatavärdet inte kan bestämmas från raden. Protokollets namn, förvanskat , kommer från denna slumpmässiga permutation.

Dataöverföring

Alice skickar de beräknade förvrängda tabellerna för alla grindar i kretsen till Bob. Bob behöver inmatningsetiketter för att öppna de förvanskade borden. Således väljer Alice etiketterna som motsvarar hennes inmatning $a$ och skickar dem till Bob. Till exempel, om Alices indata är $\mathbf {a} =a_{4}a_{3}a_{2}a_{1}a_{0}= 01101$ , sedan skickar hon $X_{0}^{a_{4}}$ , $X_{1}^{a_{3}}$ , $X_{1}^{a_{2}}$ , $X_{0}^{a_{1}}$ och $X_{1}^{a_{0 }}$ till Bob. Bob kommer inte att lära sig något om Alices input, $\mathbf {a}$ , eftersom etiketterna genereras slumpmässigt av Alice och de ser ut som slumpmässiga strängar för Bob.

Bob behöver också etiketterna som motsvarar hans input. Han får sina etiketter genom omedvetna överföringar för varje bit av hans input. Till exempel, om Bobs inmatning är $\mathbf {b} =b_{4}b_{3}b_{2}b_{1}b_{0}= 10100$ , Bob frågar först efter $b_{0}=0$ mellan Alices etiketter $X_{0}^{b_{0}}$ och $X_{1} ^{b_{0}}$ . Genom en 1-av-2 omedveten överföring får han $X_{0}^{b_{0}}$ och så vidare. Efter de omedvetna överföringarna kommer Alice inte att lära sig något om Bobs input och Bob kommer inte att lära sig något om de andra etiketterna.

Utvärdering

Efter dataöverföringen har Bob de förvanskade tabellerna och inmatningsetiketterna. Han går igenom alla portar en efter en och försöker dekryptera raderna i deras förvanskade bord. Han kan öppna en rad för varje tabell och hämta motsvarande utdataetikett: ${\displaystyle X ^{c}=Dec_{X^{a},X^{b}}(förvrängd\_tabell[i])} , där ≤ i ≤ 3 {\displaystyle 0\$ leq $}$ . Han fortsätter utvärderingen tills han når utdataetiketterna.

Avslöjande utgång

Efter utvärderingen får Bob utdataetiketten, $X^{c}$ , och Alice känner till dess mappning till booleskt värde eftersom hon har båda etiketterna: $X_{0}^{c}$ och $X_{1}^{c}$ . Antingen kan Alice dela sin information till Bob eller så kan Bob avslöja resultatet för Alice så att en eller båda lär sig utdata.

Optimering

Peka-och-permutera

I denna optimering genererar Alice en slumpmässig bit, $s$ , kallad select bit för varje tråd $w^{a}$ . Hon ställer sedan in den första biten av etikett 0, $X_{0}^{a}$ till $s$ och den första biten av etikett 1, $X_{1}^ {a}$ , till ${\bar {s}}$ ( INTE av $s$ ). Hon sorterar sedan, istället för att permutera slumpmässigt, den förvrängda tabellen enligt ingångsvalbiten. På så sätt behöver Bob inte testa alla fyra raderna i tabellen för att hitta den korrekta, eftersom han har inmatningsetiketterna och kan hitta rätt rad och dekryptera den med ett försök. Detta minskar utvärderingsbelastningen med 4 gånger. Det avslöjar inte heller något om utdatavärdet eftersom de valda bitarna genereras slumpmässigt.

Radminskning

Denna optimering minskar storleken på förvanskade tabeller från 4 rader till 3 rader. Här, istället för att generera en etikett för utgångsledningen på en grind slumpmässigt, genererar Alice den med hjälp av en funktion av ingångsetiketterna. Hon genererar utdataetiketterna så att den första posten i den förvanskade tabellen blir 0 och inte längre behöver skickas:

${\begin{aligned}&Enc_{X_{0}^{a},X_{0}^{b}}(X_{0}^{c})=0\\&X_{0}^{c }=Dec_{X_{0}^{a},X_{0}^{b}}(0).\end{aligned}}$

Gratis XOR

I denna optimering genererar Alice ett globalt slumpmässigt (k-1)-bitvärde $R$ som hålls hemligt. Under förvrängningen av ingångsgrindarna $w^{a}$ och $w^{b}$ genererar hon bara etiketterna $(X_{0) }^{a},X_{0}^{b})$ och beräknar de andra etiketterna som $X_{1}^{a}=X_{0} ^{a}\oplus (R\parallel 1)$ och $X_{1}^{b}=X_{0}^{b}\oplus (R \parallell 1)$ . Med dessa värden är etiketten för en XOR-grinds utgångstråd $w^{c}$ med ingångsledningar $w^{a}$ , $w^{b}$ satt till $X^{c}=X^{a}\oplus X^{b}$ . Säkerhetsbeviset i Random Oracle-modellen för denna optimering ges i Free-XOR-dokumentet.

Inblandning

Gratis XOR-optimering innebär en viktig punkt att mängden dataöverföring (kommunikation) och antalet kryptering och dekryptering (beräkning) av det förvanskade kretsprotokollet endast beror på antalet OCH-grindar i den booleska kretsen , inte XOR-grindarna . Sålunda, mellan två booleska kretsar som representerar samma funktion, är den med det mindre antalet OCH-grindar att föredra.

Blockchiffer med fast nyckel

AES med fast nyckel istället för dyr kryptografisk hashfunktion som SHA-2 . I detta förvrängningsschema som är kompatibelt med Free XOR och Row Reduction , krypteras utmatningsnyckeln $X^{c}$ med inmatningstoken $\displaystyle X^{a}}$ $X^{b}$ och med krypteringsfunktionen ${\displaystyle Enc(X^{a},X ^{b},T,X^{c})=\pi (K)\oplus K\oplus X^{c}} , där K = 2 X$ a $2X^ {a}\oplus 4X^{b}\oplus T}$ , $\pi$ är ett blockchiffer med fast nyckel (t.ex. instansierat med AES ), och $T$ är ett unikt per- grindnummer (t.ex. grindidentifierare) som kallas tweak .

Hälften And

Denna optimering minskar storleken på ett förvanskat bord för OCH-grindar från 3 rader i radminskning till 2 rader. Det visas att detta är det teoretiska minimum för antalet rader i den förvanskade tabellen, för en viss klass av förvanskningstekniker.

säkerhet

Yao's Garbled Circuit är säker mot en halvärlig motståndare. Den här typen av motståndare följer protokollet och gör inget skadligt beteende, men den försöker kränka integriteten för den andra partens input genom att granska meddelandena som överförs i protokollet.

Det är mer utmanande att göra detta protokoll säkert mot en illvillig motståndare som avviker från protokollet. En av de första lösningarna för att göra protokollet säkert mot illvilliga motståndare är att använda noll-kunskapsbevis för att förhindra skadliga aktiviteter under protokollet. I åratal ansågs detta tillvägagångssätt mer som en teoretisk lösning än en praktisk lösning på grund av komplexitetens omkostnader. Men det är visat att det är möjligt att använda den med bara en liten overhead. Ett annat tillvägagångssätt är att använda flera GC för en krets och verifiera riktigheten av en delmängd av dem och sedan använda resten för beräkningen med hopp om att om garblern var skadlig skulle den upptäckas under verifieringsfasen. En annan lösning är att göra förvrängningsschemat autentiserat så att utvärderaren kan verifiera den förvrängda kretsen.

Se även

Vidare läsning

"Yaos förvrängda krets" (PDF) . CS598 . illinois.edu . Hämtad 18 oktober 2016 .