Euklids fruktträdgård

Planvy av ett hörn av Euklids fruktträdgård, där träden är märkta med x -koordinaten för deras projektion på planet x + y = 1 .

Inom matematik , informellt sett, är Euclids fruktträdgård en samling endimensionella "träd" av enhetshöjd planterade vid gitterpunkterna i en kvadrant av ett kvadratiskt galler . Mer formellt är Euklids fruktträdgård uppsättningen linjesegment från ( x , y , 0) till ( x , y , 1) , där x och y är positiva heltal .

Ett hörn av Euklids fruktträdgård, blå träd synliga från ursprunget

Perspektivvy av Euklids fruktträdgård från ursprunget. Röda träd anger rader två utanför huvuddiagonalen.

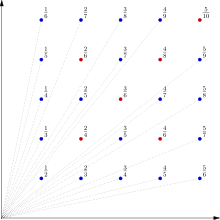
Träden som är synliga från origo är de vid gitterpunkter ( x , y , 0 ) , där x och y är coprime , dvs där fraktionen x / y är i reducerad form . Namnet Euklids fruktträdgård kommer från den euklidiska algoritmen .

Om fruktträdgården projiceras i förhållande till ursprunget på planet x + y = 1 (eller, på motsvarande sätt, ritad i perspektiv från en synvinkel vid ursprunget) bildar trädens toppar en graf över Thomaes funktion . Punkten ( x , y , 1) projicerar till

$\left({\frac {x}{x+y}},{\frac {y}{x+y}},{\frac {1}{x+y}}\right).$

Lösningen på Basel-problemet kan användas för att visa att andelen punkter i $n\times n$ rutnätet som har träd är ungefär ${\tfrac {6}{ \pi ^{2}}}$ och att felet för denna approximation går till noll i gränsen när n går till oändlighet.

Se även

• Problem med ogenomskinlig skog

externa länkar

• Euclid's Orchard, klass 9-11 aktiviteter och problemblad, Texas Instruments Inc.
• Projekt Euler-relaterat problem