En* sökalgoritm

Ej att förväxla med Skytten A* .

Klass	Sökalgoritm
Datastruktur	Graf
Prestanda i värsta fall	$O(|E|)=O(b^{d})$
Värsta tänkbara utrymmeskomplexitet	$O(|V|)=O(b^{d})$

A* (uttalas "A-stjärna") är en algoritm för genomgång av grafer och sökvägar , som används inom många områden av datavetenskap på grund av dess fullständighet, optimalitet och optimala effektivitet. En stor praktisk nackdel är dess $O(b^{d})$ rymdkomplexitet , eftersom den lagrar alla noder i minnet. Sålunda, i praktiska resedirigeringssystem , överträffas den i allmänhet av algoritmer som kan förbearbeta grafen för att uppnå bättre prestanda, såväl som minnesbundna tillvägagångssätt; dock är A* fortfarande den bästa lösningen i många fall.

Peter Hart , Nils Nilsson och Bertram Raphael från Stanford Research Institute (numera SRI International ) publicerade algoritmen första gången 1968. Den kan ses som en förlängning av Dijkstras algoritm . A* uppnår bättre prestanda genom att använda heuristik för att styra sökningen.

Jämfört med Dijkstras algoritm, hittar A*-algoritmen endast den kortaste vägen från en specificerad källa till ett specificerat mål, och inte det kortaste vägträdet från en specificerad källa till alla möjliga mål. Detta är en nödvändig avvägning för att använda en specifik målinriktad heuristik. För Dijkstras algoritm, eftersom hela trädet med den kortaste vägen genereras, är varje nod ett mål, och det kan inte finnas någon specifik målriktad heuristik.

Historia

A* uppfanns av forskare som arbetar med Shakey the Robots vägplanering.

A* skapades som en del av Shakey-projektet , som hade som syfte att bygga en mobil robot som kunde planera sina egna handlingar. Nils Nilsson föreslog ursprungligen att använda Graph Traverser-algoritmen för Shakeys vägplanering. Graph Traverser styrs av en heuristisk funktion h ( n ) , det uppskattade avståndet från nod n till målnoden: den ignorerar helt g ( n ) , avståndet från startnoden till n . Bertram Raphael föreslog att man skulle använda summan, g ( n ) + h ( n ) . Peter Hart uppfann de begrepp vi nu kallar tillåtlighet och konsistens av heuristiska funktioner. A* designades ursprungligen för att hitta lägsta kostnadsvägar när kostnaden för en väg är summan av dess kostnader, men det har visat sig att A* kan användas för att hitta optimala vägar för alla problem som uppfyller villkoren för en kostnadsalgebra.

Det ursprungliga A*-papperet från 1968 innehöll ett teorem som säger att ingen A*-liknande algoritm skulle kunna expandera färre noder än A* om den heuristiska funktionen är konsekvent och A*:s jävsbrytande regel är lämpligt vald. En ″korrigering″ publicerades några år senare som hävdade att konsistens inte krävdes, men detta visade sig vara falskt i Dechter och Pearls definitiva studie av A*s optimalitet (nu kallad optimal effektivitet), som gav ett exempel på A* med en heuristik som var tillåten men inte konsekvent utökade godtyckligt fler noder än en alternativ A*-liknande algoritm.

Beskrivning

En* sökvägsalgoritm som navigerar runt en slumpmässigt genererad labyrint

Illustration av A*-sökning för att hitta en väg mellan två punkter på en graf. Från vänster till höger används en heuristik som föredrar punkter närmare målet alltmer.

A* är en informerad sökalgoritm , eller en bäst-först-sökning , vilket betyder att den är formulerad i termer av viktade grafer : utgående från en specifik startnod i en graf, syftar den till att hitta en väg till den givna målnoden som har den minsta kostnad (minsta tillryggalagda sträcka, kortaste tid, etc.). Den gör detta genom att upprätthålla ett träd av vägar som kommer från startnoden och förlänga dessa vägar en kant i taget tills dess avslutningskriterium är uppfyllt.

Vid varje iteration av dess huvudslinga måste A* bestämma vilken av dess vägar som ska förlängas. Den gör det baserat på kostnaden för vägen och en uppskattning av kostnaden som krävs för att förlänga vägen hela vägen till målet. Specifikt väljer A* den sökväg som minimerar

$f(n)=g(n)+h(n)$

där n är nästa nod på vägen, g ( n ) är kostnaden för vägen från startnoden till n , och h ( n ) är en heuristisk funktion som uppskattar kostnaden för den billigaste vägen från n till målet. A* avslutas när vägen den väljer att förlänga är en väg från start till mål eller om det inte finns några vägar som kan förlängas. Den heuristiska funktionen är problemspecifik. Om den heuristiska funktionen är tillåten – vilket innebär att den aldrig överskattar den faktiska kostnaden för att nå målet – kommer A* garanterat att returnera en minsta kostnadsväg från start till mål.

Typiska implementeringar av A* använder en prioritetskö för att utföra det upprepade urvalet av lägsta (uppskattade) kostnadsnoder för att expandera. Denna prioritetskö är känd som den öppna uppsättningen , frans eller gräns. Vid varje steg i algoritmen tas noden med det lägsta f ( x ) -värdet bort från kön, f- och g -värdena för dess grannar uppdateras i enlighet med detta, och dessa grannar läggs till i kön. Algoritmen fortsätter tills en borttagen nod (alltså noden med det lägsta f- värdet av alla fransnoder) är en målnod. F- värdet för det målet är då också kostnaden för den kortaste vägen, eftersom h vid målet är noll i en tillåten heuristik.

Algoritmen som beskrivits hittills ger oss bara längden på den kortaste vägen. För att hitta den faktiska sekvensen av steg kan algoritmen enkelt revideras så att varje nod på vägen håller reda på sin föregångare. Efter att denna algoritm har körts kommer slutnoden att peka på sin föregångare, och så vidare, tills någon nods föregångare är startnoden.

Som ett exempel, när du söker efter den kortaste rutten på en karta, kan h ( x ) representera det raka avståndet till målet, eftersom det är fysiskt det minsta möjliga avståndet mellan två punkter. För en rutnätskarta från ett videospel blir användningen av Manhattan-avståndet eller det oktila avståndet bättre beroende på uppsättningen av tillgängliga rörelser (4-vägs eller 8-vägs).

Om heuristiken h uppfyller det ytterligare villkoret h ( x ) ≤ d ( x , y ) + h ( y ) för varje kant ( x , y ) på grafen (där d anger längden på den kanten), så kallas h monoton eller konsekvent . Med en konsekvent heuristik är A* garanterat att hitta en optimal väg utan att bearbeta någon nod mer än en gång d' ( x , y ) = d ( x , y ) + h ( y ) − h ( x ) och A* motsvarar att köra Dijkstras algoritm med den reducerade kostnaden .

Pseudokod

Följande pseudokod beskriver algoritmen:

  
      
       
          
        
     



   
    
    
    
      

    
    
        

    
           
      0

    
    
           
      

        
        
                  
           
              

        
            
            
            
                 
               
                
                  
                  
                    
                    
                    

    
      funktion  reconstruct_path  (  cameFrom  ,  current  )  total_path  :=  {current}  medan  aktuell  i  cameFrom  .  Nycklar  :  aktuell  :=  kom Från  [  aktuell  ]  total_path  .  prepend  (  aktuell  )  return  total_path  // A* hittar en väg från start till mål.  // h är den heuristiska funktionen. h(n) uppskattar kostnaden för att nå målet från nod n.   function  A_Star  (  start  ,  goal  ,  h  )  // Uppsättningen av upptäckta noder som kan behöva (åter)expanderas.  // Initialt är bara startnoden känd.  // Detta implementeras vanligtvis som en min-hög eller prioritetskö snarare än en hash-uppsättning.  openSet  :=  {start}  // För nod n, cameFrom[n] är noden omedelbart före den på den billigaste vägen från start  // till n som för närvarande är känd.  cameFrom  :=  en  tom  karta  // För nod n är gScore[n] kostnaden för den billigaste vägen från start till n som för närvarande är känd.  gScore  :=  karta  med  standardvärdet  på  Infinity  gScore  [  start  ]  :=  // För nod n, fScore[n] := gScore[n] + h(n)  .  fScore[n] representerar vår nuvarande bästa gissning om  // hur billig en väg kan vara från början till slut om den går genom n.  fScore  :=  karta  med  standardvärde  på  Infinity  fScore  [  start  ]  :=  h  (  start  )  medan  openSet  inte  är  tom // Denna operation kan ske i O(Log(N)) tid   om  openSet är en min-hög eller en prioritetskö  current  :  =  noden  i  openSet  som  har  det  lägsta  fScore  []  värdet  om  aktuell  =  målretur  reconstruct_path  (  cameFrom  ,  current  )  openSet  .  Ta bort  (  aktuell  )  för  varje  granne  till  ström  // d(ström, granne) är vikten av kanten från ström till granne //  tentative_gScore är avståndet från start till granne genom nuvarande  tentative_gScore  :=  gScore  [  aktuell  ]  +  d  (  current  ,  neighbor  )  if  tentative_gScore  <  gScore  [  neighbor  ]  // Denna väg till granne är bättre än någon tidigare. Spela in det!   komFrån  [  granne  ]  :=  nuvarande  gScore  [  granne  ]  :=  tentative_gPoäng  fScore  [  granne  ]  :=  tentative_gPoäng  +  h  (  granne  )  om  granne  inte  är i  openSet  openSet  .  lägg till  (  granne  )  // Öppen uppsättning är tom men målet nåddes aldrig  retur  misslyckande 

Anmärkning: I denna pseudokod, om en nod nås av en sökväg, tas bort från openSet och därefter nås av en billigare sökväg, kommer den att läggas till i openSet igen. Detta är viktigt för att garantera att sökvägen som returneras är optimal om den heuristiska funktionen är tillåten men inte konsekvent . Om heuristiken är konsekvent, när en nod tas bort från openSet är sökvägen till den garanterat optimal så att testet ' tentative_gScore < gScore[granne] ' alltid misslyckas om noden nås igen.

Illustration av A*-sökning för att hitta vägen från en startnod till en målnod i ett robotrörelseplaneringsproblem . De tomma cirklarna representerar noderna i den öppna uppsättningen , dvs de som återstår att utforska, och de fyllda är i den slutna uppsättningen. Färg på varje stängd nod indikerar avståndet från målet: ju grönare, desto närmare. Man kan först se A* röra sig i en rak linje i riktning mot målet, sedan när den träffar hindret utforskar den alternativa vägar genom noderna från det öppna setet.

Se även: Dijkstras algoritm

Exempel

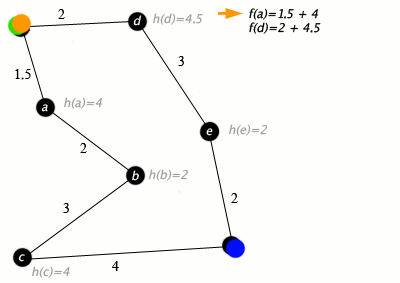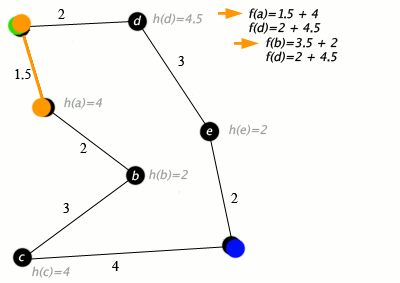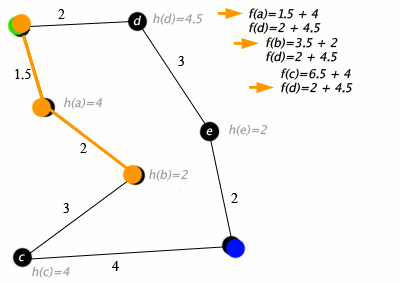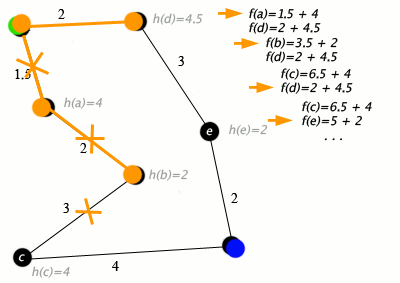
Ett exempel på en A*-algoritm i aktion där noder är städer kopplade till vägar och h(x) är det raka avståndet till målpunkten:

Nyckel: grön: start; blått: mål; orange: besökt

A*-algoritmen har också verkliga tillämpningar. I det här exemplet är kanter järnvägar och h(x) är storcirkelavståndet ( kortast möjliga avstånd på en sfär) till målet. Algoritmen söker efter en väg mellan Washington, DC och Los Angeles.

Genomförande detaljer

Det finns ett antal enkla optimeringar eller implementeringsdetaljer som avsevärt kan påverka prestandan för en A*-implementering. Den första detaljen att notera är att hur prioritetskön hanterar kopplingar kan ha en betydande effekt på prestandan i vissa situationer. Om banden bryts så att kön beter sig på ett LIFO- sätt, kommer A* att bete sig som djup-först-sökning bland lika kostnadsvägar (undviker att utforska mer än en lika optimal lösning).

När en sökväg krävs i slutet av sökningen är det vanligt att för varje nod ha en referens till den nodens förälder. I slutet av sökningen kan dessa referenser användas för att återställa den optimala sökvägen. Om dessa referenser behålls kan det vara viktigt att samma nod inte visas i prioritetskön mer än en gång (varje post motsvarar en annan väg till noden, och var och en med olika kostnad). En standardmetod här är att kontrollera om en nod som ska läggas till redan dyker upp i prioritetskön. Om den gör det ändras prioritets- och överordnade pekare för att motsvara den billigare sökvägen. En standard binär högbaserad prioritetskö stöder inte direkt operationen att söka efter ett av dess element, men den kan utökas med en hashtabell som mappar element till deras position i högen, vilket gör att denna minskningsprioritetsoperation kan utföras i logaritmisk tid. Alternativt kan en Fibonacci-hög utföra samma operationer med minskad prioritet under konstant amorterad tid .

Speciella fall

Dijkstras algoritm , som ett annat exempel på en enhetlig kostnadssökalgoritm, kan ses som ett specialfall av A* där $h(x)=0$ för alla x . Allmän djup-först-sökning kan implementeras med hjälp av A* genom att beakta att det finns en global räknare C initierad med ett mycket stort värde. Varje gång vi bearbetar en nod tilldelar vi C till alla dess nyupptäckta grannar. Efter varje enskilt uppdrag minskar vi räknaren C med ett. Således ju tidigare en nod upptäcks, desto högre är dess ${\displaystyle h(x)}-$ värde. Både Dijkstras algoritm och djup-först-sökning kan implementeras mer effektivt utan att inkludera ett ${\displaystyle h(x)}-$ värde vid varje nod.

Egenskaper

Uppsägning och fullständighet

På finita grafer med icke-negativa kantvikter kommer A* garanterat att avslutas och är komplett , dvs den kommer alltid att hitta en lösning (en väg från start till mål) om en sådan finns. På oändliga grafer med en ändlig förgreningsfaktor och kantkostnader som är avgränsade från noll ( ${\textstyle d(x,y)>\varepsilon >0}$ för vissa fasta $\ varepsilon$ ), A* kommer garanterat att avslutas endast om det finns en lösning.

Tillåtlighet

En sökalgoritm sägs vara tillåten om den garanterat ger en optimal lösning. Om den heuristiska funktionen som används av A* är tillåten är A* tillåten. Ett intuitivt ″bevis″ på detta är följande:

När A* avslutar sin sökning har den hittat en väg från start till mål vars faktiska kostnad är lägre än den uppskattade kostnaden för en väg från start till mål genom vilken öppen nod som helst (nodens f {\displaystyle f} $)$ . När heuristiken är tillåten är dessa uppskattningar optimistiska (inte riktigt – se nästa stycke), så A* kan säkert ignorera dessa noder eftersom de omöjligen kan leda till en billigare lösning än den den redan har. Med andra ord, A* kommer aldrig att förbise möjligheten av en billigare väg från start till mål och så kommer den att fortsätta söka tills det inte finns några sådana möjligheter.

Själva beviset är lite mer involverat eftersom $f$ -värdena för öppna noder inte garanteras vara optimistiska även om heuristiken är tillåten. Detta beror på att $g$ -värdena för öppna noder inte garanteras vara optimala, så summan $g+h$ är inte garanterat optimistisk.

Optimalitet och konsekvens

Algoritm A är optimalt effektiv med avseende på en uppsättning alternativa algoritmer Alts på en uppsättning problem P om för varje problem P i P och varje algoritm A′ i Alts , uppsättningen av noder expanderade med A vid lösning av P är en delmängd (ev. lika) av uppsättningen av noder utökad med A′ vid lösning av P. Den definitiva studien av den optimala effektiviteten för A* beror på Rina Dechter och Judea Pearl. De ansåg en mängd olika definitioner av Alts och P i kombination med att A*:s heuristik bara är tillåten eller är både konsekvent och tillåtlig. Det mest intressanta positiva resultatet de bevisade är att A*, med en konsekvent heuristik, är optimalt effektiv med avseende på alla tillåtna A*-liknande sökalgoritmer på alla ″icke-patologiska″ sökproblem. Grovt sett är deras föreställning om det icke-patologiska problemet vad vi nu menar med "upp till oavgjort". Detta resultat gäller inte om A*:s heuristik är tillåten men inte konsekvent. I det fallet visade Dechter och Pearl att det finns tillåtna A*-liknande algoritmer som kan expandera godtyckligt färre noder än A* på vissa icke-patologiska problem.

Optimal effektivitet handlar om uppsättningen noder expanderade, inte antalet nodexpansions (antalet iterationer av A*s huvudslinga). När heuristiken som används är tillåten men inte konsekvent, är det möjligt att en nod utökas med A* många gånger, ett exponentiellt antal gånger i värsta fall. Under sådana omständigheter kan Dijkstras algoritm överträffa A* med stor marginal. Nyare forskning fann dock att detta patologiska fall endast inträffar i vissa konstruerade situationer där sökgrafens kantvikt är exponentiell i storleken på grafen och att vissa inkonsekventa (men tillåtliga) heuristik kan leda till ett minskat antal nodexpansioner i A*-sökningar.

Begränsad avkoppling

En* sökning som använder en heuristik som är 5.0(=ε) gånger en konsekvent heuristik och erhåller en suboptimal väg.

Samtidigt som tillåtlighetskriteriet garanterar en optimal lösningsväg, innebär det också att A* måste undersöka alla lika meriterande vägar för att hitta den optimala vägen. För att beräkna ungefärliga kortaste vägar är det möjligt att påskynda sökningen på bekostnad av optimaliteten genom att lätta på tillåtlighetskriteriet. Ofta vill vi binda denna avslappning, så att vi kan garantera att lösningsvägen inte är sämre än (1 + ε ) gånger den optimala lösningsvägen. Denna nya garanti kallas ε -tillåten.

Det finns ett antal ε- godkända algoritmer:

• Viktade A*/statiska viktningar. Om h _a ( n ) är en tillåten heuristisk funktion använder man i den viktade versionen av A*-sökningen h _w ( n ) = ε h _a ( n ) , ε > 1 som heuristisk funktion, och utför A*-sökningen som vanligt (vilket så småningom sker snabbare än att använda h _a eftersom färre noder expanderas). Sökvägen som därför hittas av sökalgoritmen kan ha en kostnad på högst ε gånger den för den lägsta kostnadsvägen i grafen.
• Dynamisk viktning använder kostnadsfunktionen $f(n)=g(n)+(1+\varepsilon w(n) ))h(n)$ , där ${\displaystyle w(n)={\begin{cases}1-{\frac {d (n)}{N}}&d(n)\leq N\\0&{\text{annars}}\end{cases}}} , och där d ( n ) {\displaystyle$ d $är$ djupet av sökningen och N är den förväntade längden på lösningsvägen.
• Samplad dynamisk viktning använder sampling av noder för att bättre uppskatta och försvaga det heuristiska felet.
• $A_{\varepsilon }^{*}$ . använder två heuristiska funktioner. Den första är FOCAL-listan, som används för att välja kandidatnoder, och den andra hF _. används för att välja den mest lovande noden från FOCAL-listan
• A _ε väljer noder med funktionen ${\displaystyle Af(n)+Bh_{F}(n)} ,$ där A och B är konstanter. Om inga noder kan väljas $Cf(n)+Dh_{F}(n)$ algoritmen att backa med funktionen C och D är konstanter.
• AlphA* försöker främja djup-först exploatering genom att föredra nyligen utökade noder. AlphA* använder kostnadsfunktionen $f_{\alpha }(n)=(1+w_{\alpha }(n))f (n)$ , där ${\displaystyle w_{\alpha }(n)={\begin{cases}\lambda &g (\pi (n))\leq g({\tilde {n}})\\\Lambda &{\text{annars}}\end{fall}}} , där λ$ och Λ är konstanter med ${ \displaystyle \lambda \leq \Lambda } ,$ π ( n ) är föräldern till n , och ñ är den senast expanderade noden.

Komplexitet

Tidskomplexiteten för A* beror på heuristiken . I värsta fallet med ett obegränsat sökutrymme är antalet expanderade noder exponentiellt i lösningens djup (den kortaste vägen) d : O ( b ^d ) , där b är förgreningsfaktorn (det genomsnittliga antalet efterföljare per tillstånd ). Detta förutsätter att ett måltillstånd överhuvudtaget existerar och är nåbart från starttillståndet; om det inte är det, och tillståndsutrymmet är oändligt, kommer algoritmen inte att avslutas.

Den heuristiska funktionen har en stor effekt på det praktiska utförandet av A*-sökning, eftersom en bra heuristik tillåter A* att beskära bort många av de b ^d -noder som en oinformerad sökning skulle expandera. Dess kvalitet kan uttryckas i termer av den effektiva förgreningsfaktorn b * , som kan bestämmas empiriskt för en probleminstans genom att mäta antalet noder som genereras av expansion, N , och djupet av lösningen, och sedan lösa

$N+1=1+b^{*}+(b^{*})^{2}+\dots +(b^{*})^{d}.$

Bra heuristik är de med låg effektiv förgreningsfaktor (det optimala är b * = 1 ).

Tidskomplexiteten är polynom när sökutrymmet är ett träd, det finns ett enda måltillstånd och den heuristiska funktionen h uppfyller följande villkor:

$|h(x)-h^{*}(x)|=O(\log h^{*}(x))$

där h ^* är den optimala heuristiken, den exakta kostnaden för att komma från x till målet. Med andra ord kommer felet för h inte att växa snabbare än logaritmen för den "perfekta heuristiken" h ^* som returnerar det verkliga avståndet från x till målet.

Rymdkomplexiteten för A* är ungefär densamma som för alla andra grafsökningsalgoritmer, eftersom den håller alla genererade noder i minnet . I praktiken visar sig detta vara den största nackdelen med A*-sökningen, vilket leder till utvecklingen av minnesbundna heuristiska sökningar, såsom Iterativ fördjupning A* , minnesgränsad A* och SMA* .

Ansökningar

A* används ofta för det vanliga sökvägsproblemet i applikationer som videospel, men designades ursprungligen som en allmän grafövergångsalgoritm. Den hittar tillämpningar i olika problem, inklusive problemet med att analysera med stokastisk grammatik i NLP . Andra fall inkluderar en informationssökning med onlineinlärning.

Relationer till andra algoritmer

Det som skiljer A* från en girig bäst-först-sökalgoritm är att den tar hänsyn till kostnaden/avståndet som redan har rests, g ( n ) .

Vissa vanliga varianter av Dijkstras algoritm kan ses som ett specialfall av A* där heuristiken $h(n)=0$ för alla noder; i sin tur är både Dijkstra och A* specialfall av dynamisk programmering . A* i sig är ett specialfall av en generalisering av branch och bound .

Varianter

• När som helst A*
• Block A*
• D*
• Fält D*
• Frans
• Fringe Saving A* (FSA*)
• Generalized Adaptive A* (GAA*)
• Inkrementell heuristisk sökning
• Reducerad A*
• Iterativ fördjupning A* (IDA*)
• Hoppa punkt sökning
• Livslångt planering A* (LPA*)
• Ny dubbelriktad A* (NBA*)
• Förenklat minnes begränsat A* (SMA*)
• Theta*

A* kan också anpassas till en dubbelriktad sökalgoritm . Särskild försiktighet måste iakttas för stoppkriteriet.

Se även

• Utöka första sökningen
• Djup-första sökning
• Banplanering med valfri vinkel , sök efter banor som inte är begränsade till att röra sig längs grafens kanter utan snarare kan ta vilken vinkel som helst

Vidare läsning

•   Nilsson, NJ (1980). Principer för artificiell intelligens . Palo Alto, Kalifornien: Tioga Publishing Company. ISBN 978-0-935382-01-3 .

externa länkar

• Variation på A* kallas Hierarchical Path-Finding A* (HPA*)
• Brian Grinstead. "A* sökalgoritm i JavaScript (uppdaterad)" . Arkiverad från originalet den 15 februari 2020 . Hämtad 8 februari 2021 .