Djupt trosnätverk

Schematisk översikt av ett djupt trosnät. Pilar representerar riktade kopplingar i den grafiska modellen som nätet representerar.

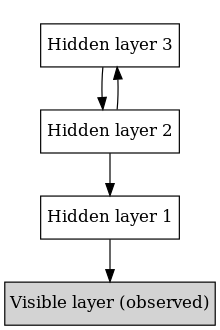
Inom maskininlärning är ett deep belief network ( DBN ) en generativ grafisk modell , eller alternativt en klass av djupa neurala nätverk , sammansatt av flera lager av latenta variabler ("dolda enheter"), med kopplingar mellan lagren men inte mellan enheter inom varje lager.

När den tränas på en uppsättning exempel utan övervakning kan en DBN lära sig att sannolikt rekonstruera sina indata. Skikten fungerar sedan som funktionsdetektorer . Efter detta inlärningssteg kan ett DBN vidareutbildas med handledning för att utföra klassificering .

DBN kan ses som en sammansättning av enkla, oövervakade nätverk som begränsade Boltzmann-maskiner (RBM) eller autoencoders , där varje delnätverks dolda lager fungerar som det synliga lagret för nästa. En RBM är en oriktad , generativ energibaserad modell med ett "synligt" indatalager och ett dolt lager och kopplingar mellan men inte inom lager. Denna sammansättning leder till en snabb, lager-för-lager oövervakad träningsprocedur, där kontrastiv divergens appliceras på varje delnätverk i tur och ordning, med början från det "lägsta" paret av lager (det lägsta synliga lagret är en träningsuppsättning ).

Observationen att DBN kan tränas girigt , ett lager i taget, ledde till en av de första effektiva djupinlärningsalgoritmerna . Sammantaget finns det många attraktiva implementeringar och användningar av DBN i verkliga tillämpningar och scenarier (t.ex. elektroencefalografi , läkemedelsupptäckt) .

Träning

En begränsad Boltzmann-maskin (RBM) med fullt anslutna synliga och dolda enheter. Observera att det inte finns några dolda, dolda eller synliga anslutningar.

Den träningsmetod för RBM som Geoffrey Hinton föreslagit för användning med träningsmodeller för "Product of Expert" kallas kontrastiv divergens (CD). CD ger en uppskattning av den maximala sannolikhetsmetoden som helst skulle användas för att lära sig vikterna. Vid träning av en enda RBM utförs viktuppdateringar med gradientnedstigning via följande ekvation: ${\ displaystyle w_{ij}(t+1)=w_{ij}(t)+\eta {\frac {\partial \log(p(v))}{\partial w_{ij}}}}$

där, $p(v)$ är sannolikheten för en synlig vektor, som ges av $p(v) ={\frac {1}{Z}}\sum _{h}e^{-E(v,h)}$ . $Z$ är partitionsfunktionen (används för normalisering) och $E(v,h)$ är energifunktionen som är tilldelad till nätverkets tillstånd. En lägre energi indikerar att nätverket är i en mer "önskvärd" konfiguration. Gradienten ${\frac {\partial \log(p(v))}{\partial w_{ij}}}$ har den enkla formen $\langle v_{i}h_{j}\rangle _{\text{data}}-\langle v_{i}h_{j}\rangle _{ \text{modell}}$ där $\langle \cdots \rangle _{p}$ representerar medelvärden med avseende på fördelningen $p$ . Problemet uppstår vid sampling $\langle v_{i}h_{j}\rangle _{\text{modell}}$ eftersom detta kräver utökad alternerande Gibbs-sampling . CD ersätter detta steg genom att köra omväxlande Gibbs-sampling för $n$ steg (värden på $n=1$ fungerar bra). Efter $n$ steg samplas data och det samplet används istället för $\langle v_{i}h_{j}\rangle _{\text{model} }$ . CD-proceduren fungerar enligt följande:

Initiera de synliga enheterna till en träningsvektor.
Uppdatera de dolda enheterna parallellt givet de synliga enheterna: $p(h_{j}=1\mid {\textbf {V}})=\sigma (b_{j}+\sum _{i}v_{i}w_{ij})$ . $\sigma$ är sigmoidfunktionen och $b_{j}$ är bias för $h_{j}$ .
Uppdatera de synliga enheterna parallellt givet de dolda enheterna: $p(v_{i}=1\mid {\textbf {H}})=\sigma (a_{i}+\summa _{j}h_{j}w_{ij})$ . $a_{i}$ är bias av $v_{i}$ . Detta kallas "rekonstruktionssteget".
Uppdatera de dolda enheterna på nytt parallellt givet de rekonstruerade synliga enheterna med samma ekvation som i steg 2.
Utför viktuppdateringen: $\Delta w_{ij}\propto \langle v_{i}h_{j}\rangle _{ \text{data}}-\langle v_{i}h_{j}\rangle _{\text{rekonstruktion}}$ .

När väl en RBM är tränad, "staplas" en annan RBM ovanpå den och tar dess input från det slutliga tränade lagret. Det nya synliga lagret initieras till en träningsvektor, och värden för enheterna i de redan tränade lagren tilldelas med hjälp av aktuella vikter och förspänningar. Den nya RBM tränas sedan med proceduren ovan. Hela denna process upprepas tills det önskade stoppkriteriet är uppfyllt.

Även om approximationen av CD till maximal sannolikhet är grov (följer inte gradienten för någon funktion), är den empiriskt effektiv.

Se även

externa länkar

"Deep Belief Networks" . Deep Learning Tutorials .
"Deep Belief Network Exempel" . Deeplearning4j självstudier . Arkiverad från originalet 2016-10-03 . Hämtad 2015-02-22 .