Differentialremskiva
En differentialremskiva - även kallad "Weston differentialremskiva", ibland "differentialtelfer", "kedjetelfer" eller i vardagsspråk "kedjefall" - används för att manuellt lyfta mycket tunga föremål som bilmotorer . Den drivs genom att dra i den slappa delen av en kontinuerlig kedja som lindar runt två remskivor på en gemensam axel. (De två remskivorna är sammanfogade så att de roterar som en enhet på den enda axeln som de delar.) Den relativa storleken på de två anslutna remskivorna bestämmer den maximala vikten som kan lyftas för hand. Om remskivans radier är tillräckligt nära, kommer lasten att förbli på plats (och inte sänkas under tyngdkraften) tills kedjan dras.
Historia
Differentialremskivan uppfanns 1854 av Thomas Aldridge Weston från King's Norton, England.
Remskivorna tillverkades i samarbete med Richard och George Tangye. Enligt Richard Tangyes självbiografi utvecklades Weston differentialremskiva från det kinesiska ankarspelet , med en ändlös kedja som ersatte den ändliga längden på repet. Han hävdade att många ingenjörsfirmor medgav svårigheten att effektivt frigöra kedjan från tänderna när remskivorna svängde, men hans företag utvecklade en "pitch"-kedja som löste problemet. Marknadsförd som "Weston Differential Pulley Blocks with Patent Chain Guides", hade remskivan bra försäljning, nämligen 3000 set på 9 månader. Den visades i 5 storlekar — från 10 långa hundravikt (510 kg) till 3 långa ton (3 000 kg) — på 1862 års internationella utställning i London och fick en medalj för "ursprunglig tillämpning, praktisk användbarhet och framgång".
En järnhandlare utmanade Tangyes att remskivan hade använts i 30 år innan Westons patent men domaren William Page Wood dömde till förmån för Tangyes eftersom kopplingsmekanismen var väsentligt annorlunda än den som presenterades som bevis.
Yale Lock Company förvärvade patenträttigheterna 1876.
En stum remskiva kan lyfta mycket stora massor en kort sträcka. Den består av två fasta remskivor med olika radier som är fästa vid varandra och roterar tillsammans, en enda remskiva som bär belastningen och ett ändlöst rep som är ögla runt remskivorna. För att undvika glidning ersätts repet vanligtvis av en kedja och de anslutna remskivorna med kedjehjul .
De två sektionerna av kedjan som bär den enda remskivan utövar motsatta och ojämna vridmoment på de anslutna remskivorna, så att endast skillnaden mellan dessa vridmoment måste kompenseras manuellt genom att dra i den lösa delen av kedjan. Detta leder till en mekanisk fördel : kraften som krävs för att lyfta en last är bara en bråkdel av lastens vikt . Samtidigt är avståndet som lasten lyfts mindre än längden på kedjan som dras med samma faktor. Denna faktor (den mekaniska fördelen MA ) beror på den relativa skillnaden mellan radien r och R för de anslutna remskivorna:
Effekten på krafterna och avstånden (se figur) är kvantitativt:
Skillnaden i radier kan göras mycket liten, vilket gör den mekaniska fördelen med detta remskivasystem mycket stor. I det extrema fallet med noll skillnad i radier MA oändlig, så det behövs ingen kraft (förutom friktion) för att flytta kedjan, men att flytta kedjan kommer inte längre att lyfta lasten.
I den andra ytterligheten, när r är noll, blir systemet en enkel pistoltackling med en mekanisk fördel på 2.
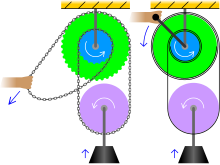
Samma princip används i ett differentiellt ankarspel , där de anslutna remskivorna ersätts av vinschar .
Beräkning av mekanisk fördel
I ovanstående grafik är de fyra segmenten i kedjan märkta med W, X, Y och Z. Storleken på deras motsvarande krafter är F W , F X , F Y respektive F Z .
Om vi antar att kedjan är masslös är F X = 0 eftersom segment X inte bär någon vikt.
Om man tar systemet i jämvikt är F W och F Y lika - om de inte var det skulle den nedre remskivan fritt vrida sig tills de var det.
Därefter är den nedåtriktade kraften som verkar på den nedre remskivan lika med de uppåtriktade krafterna som verkar på den, alltså
- F L = F W + F Y , eller 2 F W eftersom F W = F Y .
Dessutom finns det inget nettovridmoment eller moment runt den sammansatta remskivan, så vridmomentet medurs är lika med vridmomentet moturs:
- F W R + F X r = F Y r + F Z R .
Ersätter F X och F Y från ovanstående ekvationer,
- W R + 0 = FW r + FZ FWR + .
Att arrangera om ger
- F W = F Z · R / R − r .
Eftersom F W = F L / 2 ,
- F L / 2 = F Z · R / R − r .
, den mekaniska fördelen, FL F / . Z = 2 R / R − r eller 2 / 1 − r / R
________________________________________________________________________________________________________________________________________
En mycket enklare metod för att beräkna mekaniska fördelar kan uppnås genom att helt enkelt räkna och jämföra kedjelänksfickorna i de två kedjehjulen med olika storlek. Låt oss kalla antalet fickor i de två respektive kedjehjulen P1 (större) och P2 (mindre).
Vid lyftning av en last, för varje fullt varv av den dubbla kedjehjulsenheten, kommer P1 kedjelänkspar (alternativa vinkelräta länkar som passar mellan fickor) att tas upp av det större drevet medan P2 kedjelänkspar släpps av det mindre drevet, för ett nät förstärkning av P1-P2 kedjelänkspar.
Den mekaniska fördelen skulle vara lika med förhållandet mellan kedjelänkspar som krävs för varje varv och nettoförstärkningen för kedjelänkspar. Med andra ord skulle den mekaniska fördelen vara det dragavstånd som krävs för varje enhetsavstånd för förstärkning. Den mekaniska fördelen vid differentialkedjehjulsparet är lika med P1/(P1-P2).
Eftersom det finns en löpande remskiva vid lasten fördubblar detta den mekaniska fördelen med den fasta (förankrade) kedjehjulsenheten, vilket leder till en total mekanisk fördel på 2 x P1/(P1-P2).
Till exempel kan en 1-tons differentialkedjefall ha en 15-fickors och en 14-ficks kedjehjulssats. Detta skulle ge totalt 2 X 15/(15-14), eller 30:1 mekanisk fördel.


