Chang grafer

Chang-grafer
Chang-grafer
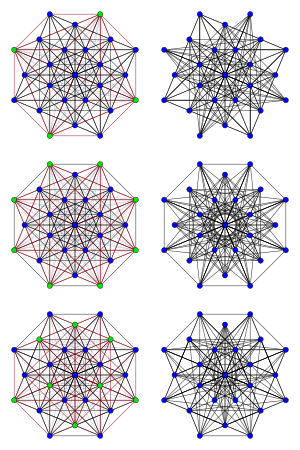	De tre Chang-graferna (höger) och kopplingsuppsättningarna som genererar dem från linjediagrammet L ( K 8 ) (grön, vänster)
Vertices	28
Kanter	168
Radie	2
Diameter	2
Omkrets	3
Automorfismer	96360384
Egenskaper	Starkt regelbunden
	Tabell över grafer och parametrar

Inom det matematiska området för grafteori är Chang -graferna en uppsättning av tre 12- reguljära oriktade grafer , var och en med 28 hörn och 168 kanter. De är starkt regelbundna , med samma parametrar och spektra som linjediagrammet L ( K ₈ ) för hela grafen K ₈ .

Var och en av dessa tre grafer kan erhållas genom att grafväxling från L ( K ₈ ). Det vill säga, en delmängd S av hörnen av L ( K ₈ ) väljs, varje kant som förbinder en vertex i S med en vertex som inte är i S tas bort från L ( K ₈ ), och en kant läggs till för varje par av hörn (med återigen en i S och en inte i S ) som inte redan var förbundna med en kant. Bland de grafer som kan genereras på detta sätt är tre av dem Chang-graferna.

Chang-graferna är uppkallade efter Chang Li-Chien, som bevisade att, med endast dessa undantag, varje linjegraf i en komplett graf bestäms unikt av dess parametrar som en starkt regelbunden graf.

Se även

Shrikhande - graf , ett liknande undantag från det unika med de starkt regelbundna graferna L ( K n _{, n )}

externa länkar