Bull graf

Tjurgraf
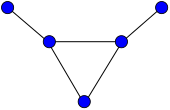Tjurgrafen
Vertices	5
Kanter	5
Radie	2
Diameter	3
Omkrets	3
Automorfismer	2 ( Z / 2Z )
Kromatiskt nummer	3
Kromatiskt index	3
Egenskaper	Planar enhetsavstånd
Tabell över grafer och parametrar

Inom det matematiska fältet för grafteorin är bull -grafen en plan oriktad graf med 5 hörn och 5 kanter, i form av en triangel med två osammanhängande hängande kanter.

Den har kromatiskt nummer 3, kromatiskt index 3, radie 2, diameter 3 och omkrets 3. Det är också en självkomplementär graf , en blockgraf , en delad graf , en intervallgraf , en klofri graf , en 1- vertex -ansluten graf och en 1 -kantsansluten graf .

Tjurfria grafer

En graf är tjurfri om den inte har någon tjur som en inducerad subgraf . De triangelfria graferna är tjurfria grafer, eftersom varje tjur innehåller en triangel. Den starka perfekta grafsatsen bevisades för tjurfria grafer långt innan dess bevis för allmänna grafer, och en polynomisk tidsigenkänningsalgoritm för tjurfria perfekta grafer är känd.

Maria Chudnovsky och Shmuel Safra har studerat tjurfria grafer mer allmänt, och visat att varje sådan graf måste ha antingen en stor klick eller en stor oberoende uppsättning (det vill säga Erdős–Hajnal-förmodan gäller för tjurgrafen), och utvecklat en allmän strukturteori för dessa grafer.

Kromatiskt och karakteristiskt polynom

De tre graferna med ett kromatiskt polynom lika med $(x-2)(x-1)^{3}x$ .

Tjurgrafens kromatiska polynom är ( x $displaystyle (x-2)(x-1)^{3}x}$ . Två andra grafer är kromatiskt ekvivalenta med bull-grafen.

Dess karakteristiska polynom är $-x(x^{2}-x-3)(x^{2}+x-1)$ .

Dess Tutte-polynom är $x^{4}+x^{3}+x^{2}y$ .