XXTEA
|
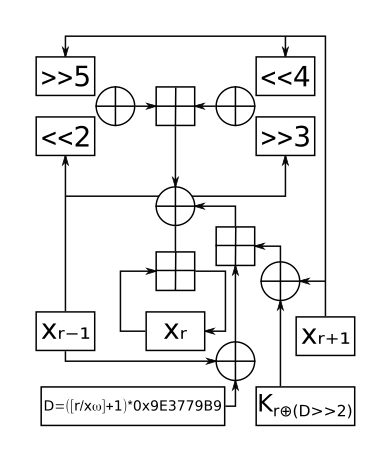
En omgång av XXTEA
| |
| General | |
|---|---|
| Designers | David Wheeler , Roger Needham |
| Först publicerad | oktober 1998 |
| Härrörande från | Block TEA |
| Chifferdetalj | |
| Nyckelstorlekar | 128 bitar |
| Blockstorlekar | godtycklig, minst två ord (64 bitar) |
| Strukturera | Obalanserat Feistel-nätverk |
| Omgångar | beror på blockstorleken; ~52+6* ord (6-32 hela cykler) |
| Bästa offentliga kryptoanalys | |
| XXTEA är sårbart för en vald-klartext-attack som kräver 2 59 frågor och försumbart arbete. | |
Inom kryptografi är Corrected Block TEA (ofta kallat XXTEA ) ett blockchiffer designat för att korrigera svagheter i det ursprungliga Block TEA .
XXTEA är sårbart för en vald-klartext-attack som kräver 2 59 frågor och försumbart arbete. Se kryptoanalys nedan.
Chifferets designers var Roger Needham och David Wheeler från Cambridge Computer Laboratory , och algoritmen presenterades i en opublicerad [ förtydligande behövs ] teknisk rapport i oktober 1998 (Wheeler och Needham, 1998) . Det är inte föremål för några patent .
Formellt sett är XXTEA ett konsekvent ofullständigt källtungt heterogent UFN (obalanserat Feistel-nätverk) blockchiffer. XXTEA arbetar på block med variabel längd som är en godtycklig multipel av 32 bitar i storlek (minst 64 bitar). Antalet hela cykler beror på blockstorleken, men det finns minst sex (stiger till 32 för små blockstorlekar). Det ursprungliga Block TEA tillämpar XTEA- rundfunktionen på varje ord i blocket och kombinerar det additivt med dess granne längst till vänster. Långsam diffusionshastighet för dekrypteringsprocessen utnyttjades omedelbart för att bryta chifferet. Corrected Block TEA använder en mer involverad rundfunktion som använder båda omedelbara grannar vid bearbetning av varje ord i blocket.
XTEA kommer sannolikt att vara effektivare än XTEA för längre meddelanden. [ citat behövs ]
Needham & Wheeler gör följande kommentarer om användningen av Block TEA:
För enkel användning och allmän säkerhet är den stora blockversionen att föredra när den är tillämplig av följande skäl.
- En enskild bitändring kommer att ändra ungefär hälften av bitarna i hela blocket, och lämnar ingen plats där ändringarna börjar.
- Det finns inget val av läge inblandat.
- Även om korrekt användning av att alltid ändra sänd data (eventuellt med ett meddelandenummer) används, ger bara identiska meddelanden samma resultat och informationsläckaget är minimalt.
- Meddelandenumret bör alltid kontrolleras eftersom denna redundans är kontrollen mot att ett slumpmässigt meddelande accepteras.
- Cut and join attacker verkar inte vara möjliga.
- Om det inte är acceptabelt att ha väldigt långa meddelanden kan de delas upp i bitar på säg 60 ord och kedjas ihop analogt med metoderna som används för DES .
Men på grund av den ofullständiga karaktären hos den runda funktionen kan två stora chiffertexter med 53 eller fler 32-bitars ord som är identiska i alla utom 12 ord hittas genom en enkel brute-force kollisionssökning som kräver 2 96−N minne , 2 N tid och 2 N +2 96−N utvalda klartexter, med andra ord med en total tids*minneskomplexitet på 2 96 , vilket faktiskt är 2 ordstorlek*fullcykler/2 för ett sådant chiffer. Det är för närvarande okänt om sådana partiella kollisioner utgör något hot mot chifferns säkerhet. Åtta hela cykler skulle höja ribban för sådan kollisionssökning över komplexiteten för parallella brute-force-attacker. [ citat behövs ]
Den ovanligt lilla storleken på XXTEA-algoritmen skulle göra den till ett genomförbart alternativ i situationer där det finns extrema begränsningar, t.ex. äldre hårdvarusystem (kanske inbyggda) där mängden tillgängligt RAM-minne är minimal, eller alternativt enkortsdatorer som Raspberry Pi , Banana Pi eller Arduino .
Kryptanalys
En attack publicerad 2010 av E. Yarrkov presenterar en vald klartextattack mot full-round XXTEA med brett block, som kräver 2 59 frågor för en blockstorlek på 212 byte eller mer, och försumbart arbete. Den är baserad på differentiell kryptoanalys .
För att chiffra "212 byte eller mer" utför algoritmen bara 6 omgångar, och noggrant utvalda bitmönster gör det möjligt att upptäcka och analysera lavineffekter. Tidningen noterar att ytterligare två omgångar (dvs. 8 omgångar istället för 6) löser detta problem.
Referens kod
Den ursprungliga formuleringen av Corrected Block TEA-algoritmen, publicerad av David Wheeler och Roger Needham, är som följer:
0 0
0
0
0
0
0
0
0
0
#define DELTA 0x9e3779b9 #define MX ((z>>5^y<<2) + (y>>3^z<<4) ^ (sum^y) + (k[p&3^e]^z)) lång btea ( lång * v , lång n , lång * k ) { unsigned long z = v [ n -1 ], y = v [ ], summa = , e , DELTA = 0x9e3779b9 ; lång p , q ; if ( n > 1 ) { /* Kodningsdel */ q = 6 + 52 / n ; while ( q -- > ) { summa += DELTA ; e = ( summa >> 2 ) & 3 ; för ( p = ; p < n -1 ; p ++ ) y = v [ p + 1 ], z = v [ p ] += MX ; y = v [ ]; z = v [ n -1 ] += MX ; } returnera ; } else if ( n < -1 ) { /* Avkodningsdel */ n = - n ; q = 6 + 52 / n ; summa = q * DELTA ; while ( summa != ) { e = ( summa >> 2 ) & 3 ; för ( p = n - 1 ; p > ; p- ) z = v [ p -1 ], y = v [ p ] -= MX ; z = v [ n -1 ]; y = v [ ] -= MX ; summa -= DELTA ; } returnera ; } returnera 1 ; }
Enligt Needham och Wheeler:
BTEA kommer att koda eller avkoda n ord som ett enda block där n > 1
- v är datavektorn med n ord
- k är nyckeln med fyra ord
- n är negativ för avkodning
- om n är noll är resultatet 1 och ingen kodning eller avkodning sker, annars är resultatet noll
- antar 32 bitars "lång" och samma endian kodning och avkodning
Observera att initieringen av z är odefinierat beteende för n < 1 vilket kan orsaka ett segmenteringsfel eller annat oönskat beteende – det skulle vara bättre placerat i "Coding Part"-blocket. I definitionen av MX skulle vissa programmerare också föredra att använda bracketing för att förtydliga operatörens företräde.
En förtydligande version inklusive dessa förbättringar är följande:
0
0
0
0
0
0
#include <stdint.h> #define DELTA 0x9e3779b9 #define MX (((z>>5^y<<2) + (y>>3^z<<4)) ^ ((sum^y) + (nyckel [(p&3)^e] ^ z))) void btea ( uint32_t * v , int n , uint32_t const key [ 4 ]) { uint32_t y , z , summa ; osignerad p , rundor , e ; if ( n > 1 ) { /* Kodningsdel */ rundor = 6 + 52 / n ; summa = ; z = v [ n -1 ]; gör { summa += DELTA ; e = ( summa >> 2 ) & 3 ; för ( p = ; p < n -1 ; p ++ ) { y = v [ p + 1 ]; z = v [ p ] += MX ; } y = v [ ]; z = v [ n -1 ] += MX ; } while ( -- rounds ); } else if ( n < -1 ) { /* Avkodningsdel */ n = - n ; rundor = 6 + 52 / n ; summa = rundor * DELTA ; y = v [ ]; do { e = ( summa >> 2 ) & 3 ; för ( p = n -1 ; p > ; p- ) { z = v [ p -1 ] ; y = v [ p ] -= MX ; } z = v [ n -1 ]; y = v [ ] -= MX ; summa -= DELTA ; } while ( -- rounds ); } }
Se även
- RC4 : Ett strömchiffer som precis som XXTEA är designat för att vara väldigt enkelt att implementera.
- XTEA : Blockera TEA:s föregångare.
- TEA : XTEAs föregångare.