Bladelementteori

Bladelementteori ( BET ) är en matematisk process som ursprungligen designades av William Froude (1878), David W. Taylor (1893) och Stefan Drzewiecki för att bestämma propellrarnas beteende . Det innebär att bryta ner ett blad i flera små delar och sedan bestämma krafterna på vart och ett av dessa små bladelement. Dessa krafter integreras sedan längs hela bladet och över ett rotorvarv för att erhålla de krafter och moment som produceras av hela propellern eller rotorn. En av de viktigaste svårigheterna ligger i att modellera den inducerade hastigheten på rotorskivan. På grund av detta kombineras bladelementteorin ofta med momentumteori för att tillhandahålla ytterligare relationer som är nödvändiga för att beskriva den inducerade hastigheten på rotorskivan, vilket producerar bladelementets momentumteori . På den mest grundläggande nivån av approximation antas en enhetlig inducerad hastighet på skivan:

v_{i}={\sqrt {{\frac {T}{A}}\cdot {\frac {1}{2\rho }}}}.

Alternativt kan variationen av den inducerade hastigheten längs radien modelleras genom att bryta ner bladet i små ringar och applicera bevarandet av massa, rörelsemängd och energi på varje ring. Detta tillvägagångssätt kallas ibland Froude – Finsterwalder -ekvationen.

Om bladelementmetoden tillämpas på helikopterrotorer i framåtflygning är det nödvändigt att beakta bladens flaxande rörelse såväl som den längsgående och laterala fördelningen av den inducerade hastigheten på rotorskivan. De enklaste modellerna för framåtflygning är första harmoniska modeller.

Enkel bladelementteori

Fig 1. Bladelement

Fig 2. Aerodynamiska krafter på ett bladelement.

Även om momentumteorin är användbar för att bestämma ideal verkningsgrad, ger den en mycket ofullständig redogörelse för verkan av skruvpropellrar och försummar bland annat vridmomentet. För att undersöka propellerns verkan mer i detalj betraktas bladen som uppbyggda av ett antal små element och luftstyrkorna på varje element beräknas. Sålunda, medan momentumteorin handlar om luftflödet, handlar bladelementteorin i första hand om krafterna på propellerbladen. Idén att analysera krafterna på elementära remsor av propellerblad publicerades först av William Froude 1878. Den utarbetades också oberoende av Drzewiecki och gavs i en bok om mekanisk flygning som publicerades i Ryssland sju år senare, 1885. Återigen, i 1907 Lanchester en något mer avancerad form av bladelementteorin utan kunskap om tidigare arbete i ämnet. Den enkla bladelementteorin brukar dock kallas för Drzewiecki-teorin, för det var Drzewiecki som satte den i praktisk form och förde den till allmän användning. Han var också den första som summerade krafterna på bladelementen för att få dragkraften och vridmomentet för en hel propeller och den första som introducerade idén att använda bärytedata för att hitta krafterna på bladelementen.

I Drzewieckis bladelementteorin anses propellern vara en skev eller vriden aerofoil , vars varje segment följer en spiralformad bana och behandlas som ett segment av en vanlig vinge. Det antas vanligtvis i den enkla teorin att vingkoefficienter som erhålls från vindtunneltester av modellvingar (vanligtvis testade med ett bildförhållande på 6) gäller direkt för propellerbladselement med samma tvärsnittsform.

Luftflödet runt varje element anses vara tvådimensionellt och därför opåverkat av de intilliggande delarna av bladet. Oberoendet av bladelementen vid varje given radie med avseende på de intilliggande elementen har fastställts teoretiskt och har även visat sig vara väsentligen sant för bladets arbetssektioner genom speciella experiment gjorda för ändamålet. Det antas också att luften passerar genom propellern utan radiellt flöde ( dvs. det finns ingen sammandragning av slipströmmen när den passerar genom propellerskivan) och att det inte finns någon bladstörning.

Aerodynamiska krafter på ett bladelement

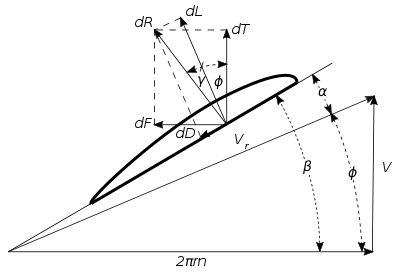
Betrakta elementet vid radien r, visat i fig. 1, som har den oändliga längden dr och bredden b. Rörelsen av elementet i en flygplanspropeller under flygning sker längs en spiralformad bana som bestäms av flygplanets framåthastighet V och den tangentiella hastigheten 2πrn för elementet i propellerskivans plan, där n representerar varven per tidsenhet. Elementets hastighet med avseende på luften Vr är då resultanten av framåt- och tangentiella hastigheter, som visas i fig. 2. Kalla vinkeln mellan elementets rörelseriktning och rotationsplanet Φ, och bladet vinkel β. Anfallsvinkeln α för elementet i förhållande till luften är då $\alpha =\beta -\phi$ .

Med vanliga vingkoefficienter är lyftkraften på elementet:

dL={\frac {1}{2}}V_{r}^{2}C_{L}b\,dr.

Låt γ vara vinkeln mellan lyftkomponenten och den resulterande kraften, eller ${\textstyle \gamma =\arctan {\frac {D}{L}}}$ . Då är den totala resulterande luftkraften på elementet:

dR={\frac {{\frac {1}{2}}V_{r}^{2}C_{L}b\,dr}{\cos \gamma }}.

Elementets dragkraft är komponenten av den resulterande kraften i propelleraxelns riktning (fig. 2), eller

{\begin{aligned}dT&=dR\cos(\ phi +\gamma )\\&={\frac {{\frac {1}{2}}V_{r}^{2}C_{L}b\cos(\phi +\gamma )}{\cos \ gamma }}dr,\end{aligned}}

och eftersom

{\textstyle V_{r}={\frac {V}{\sin \phi }}}

dT={\frac {{\frac {1}{2}}V^{2}C_{L}b\cos(\phi +\gamma )}{\sin ^{2}\phi \cos \gamma }}dr.

För bekvämlighet låt

K={\frac {C_{L}b}{\sin ^{2}\phi \cos \gamma }}

och

T_{c}=K\cos(\phi +\gamma ).

Sedan

dT={\frac {1}{2}}\rho V^{2}T_{2}\,dr,

och den totala dragkraften för propellern (av B-blad) är:

T={\frac {1}{2}}\rho V^{2}B\int _{0}^{R}T_{c}\,dr.

Med hänvisning igen till fig. 2, är tangential- eller vridmomentkraften

dF=dR\sin(\phi +\gamma ),

och vridmomentet på elementet är

dQ=r\,dR\,\sin(\phi +\gamma ),

som, om ${\textstyle Q_{c}=Kr\sin(\phi +\gamma )},$ kan skrivas

dQ={\frac {1}{2}}\rho V^{2}Q_{c}dr.

Uttrycket för hela propellerns vridmoment är därför

Q={\frac {1}{2}}\rho V^{2}B\int _{0}^{R}Q_{c}dr.

Hästkraften som absorberas av propellern, eller vridmomenthästkraften, är

QHP={\frac {2\pi nQ}{550}}

och effektiviteten är

\eta ={\frac {THP}{QHP}}={\frac {TV}{2\pi nQ}}.

Effektivitet

Fig 3. Diagram över effektivitet

På grund av variationen av bladets bredd, vinkel och vingprofil längs bladet är det inte möjligt att få ett enkelt uttryck för propellrarnas dragkraft, vridmoment och effektivitet i allmänhet. Ett enskilt element vid ungefär två tredjedelar eller tre fjärdedelar av spetsradien är dock ganska representativt för hela propellern, och det är därför intressant att undersöka uttrycket för effektiviteten hos ett enskilt element. Verkningsgraden för ett element är förhållandet mellan den användbara effekten och den absorberade effekten, eller

{\begin{aligned}\eta &={\frac {dTV}{dQ2\pi n}}\\&={\frac {dR\cos(\phi +\gamma )V}{dR\sin (\phi +\gamma )2\pi nr}}\\&={\frac {\tan \phi }{\tan(\phi +\gamma )}}.\end{aligned}}

Nu är tan Φ förhållandet mellan framåt och tangentiell hastighet, och ${\textstyle \tan \gamma ={\frac {D}{L}}}$ . Enligt den enkla bladelementteorin beror därför effektiviteten hos ett element i en propeller endast på förhållandet mellan framåt och tangentiell hastighet och på ${\textstyle {\frac {D}{L}}}$ av vingprofilsektionen.

Värdet på Φ som ger den maximala effektiviteten för ett element, som hittats genom att differentiera effektiviteten med avseende på Φ och likställa resultatet med noll, är

Fig 4. Luftflöde

\phi =45^{\circ }-{\frac {\gamma }{2}}

Fig 5. Flerplan med negativ förskjutning

Variationen av effektiviteten med 0 visas i fig. 3 för två extremvärden av y . Verkningsgraden stiger till ett maximum vid ${\textstyle 45^{\circ }-{\frac {\gamma }{2}}}$ och faller sedan till noll igen vid ${\textstyle 90^ {\circ }-\gamma }$ . Med en ${\textstyle {\frac {L}{D}}}$ på 28,6 är den maximala verkningsgraden för ett element enligt den enkla teorin 0,932, medan med en ${\textstyle {\frac {L}{ D}}}$ av 9,5 är det bara 0,812. Vid värdena Φ vid vilka de viktigaste elementen i majoriteten av propellrar arbetar (10° till 15°) är effekten av ${\textstyle {\frac {L}{D}}}$ ännu större på effektiviteten. Inom intervallet 10° till 15° indikerar kurvorna i fig. 3 att det är fördelaktigt att ha både ${\textstyle {\frac {L}{D}}}$ för bärytsektionerna och vinkeln Φ ( eller framskjutningen per varv, och följaktligen stigningen) så högt som möjligt.

Begränsningar

Enligt momentumteorin ges en hastighet till luften som passerar genom propellern, och hälften av denna hastighet ges luften när den når propellerplanet. Denna ökning av luftens hastighet när den passerar in i propellerskivan kallas inflödeshastigheten. Det finns alltid där det finns tryckavbrott i en vätska. I fallet med en vinge som rör sig horisontellt ges luften en nedåtgående hastighet, som visas i fig. 4., och teoretiskt bibringas hälften av denna hastighet framför och ovanför vingen, och den andra halvan under och bakom.

Detta inducerade nedflöde är närvarande i modellvingtesten från vilka vingkoefficienterna som används i bladelementteorin erhålls; inflödet som indikeras av momentumteorin tas därför automatiskt med i den enkla bladelementteorin. Det inducerade nedflödet är emellertid mycket olika för olika bildförhållanden, och är noll för oändliga sidförhållande. De flesta modellflygplanstester görs med rektangulära vingar med ett godtyckligt valt bildförhållande på 6, och det finns ingen anledning att anta att nedflödet i ett sådant test motsvarar inflödet för varje element i ett propellerblad. Faktum är att den allmänna slutsatsen från en uttömmande serie tester, där tryckfördelningen mättes över 12 sektioner av en modellpropeller som körs i en vindtunnel, är att lyftkoefficienten för propellerbladselementet skiljer sig avsevärt från den som uppmätts vid samma anfallsvinkel på en bäryta med bildförhållande 6. Detta är en av de största svagheterna med den enkla bladelementteorin.

En annan svaghet är att interferensen mellan propellerbladen inte beaktas. Bladens element vid en viss radie bildar en kaskad som liknar en multiplan med negativ förskjutning, som visas i fig. 4. Nära spetsarna där gapet är stort är interferensen mycket liten, men in mot bladrötterna är den ganska stor.

I verkliga propellrar finns en spetsförlust som bladelementteorin inte tar hänsyn till. Drivkraften och vridmomentet beräknade med hjälp av teorin är därför större för elementen nära spetsen än de som hittats genom experiment.

För att eliminera skaleffekt bör vindtunneltester på modellvingar köras med samma värde på Reynolds nummer (skala) som motsvarande element i propellerbladen. Aerofoil-egenskaper uppmätta i en så låg skala som till exempel en lufthastighet på 30 mph med en 3-tum. ackord aerofoil, visar egenheter som inte hittas när testerna körs i en skala som är jämförbar med den för propellerelement. Standardpropellersektionsegenskaperna som ges i fig. 11, 12, 13 och 14 erhölls från tester med höga Reynolds-tal i NACA:s tunnel med variabel densitet, och lyckligtvis är det för alla utom de tjockaste av dessa sektioner mycket liten skillnad i egenskaper vid höga och låga Reynolds-tal . Dessa värden kan användas med rimlig noggrannhet för att skala för propellrar som arbetar med spetshastigheter långt under ljudhastigheten i luft och därför relativt fria från alla effekter av kompressibilitet.

Den dåliga noggrannheten hos den enkla bladelementteorin visas mycket väl i en rapport av Durand och Lesley, där de har beräknat prestandan för ett stort antal modellpropellrar (80) och jämfört de beräknade värdena med de faktiska prestanda erhållna från tester på själva modellpropellrarna. Med författarnas ord:

Avvikelserna mellan de två uppsättningarna av resultat, samtidigt som de visar vissa delar av överensstämmelse, är på det hela taget för stora och för nyckfullt fördelade för att motivera användningen av teorin i denna enklaste form för annat än ungefärliga uppskattningar eller för jämförande syften.

Bärytorna testades i två olika vindtunnlar och i en av tunnlarna vid två olika lufthastigheter, och propelleregenskaperna som beräknats från de tre uppsättningarna med bärytedata skiljer sig med så mycket som 28 %, vilket med stor kraft illustrerar nödvändigheten av att ha bärytan. tester gjorda i rätt skala.

Trots alla dess felaktigheter har den enkla bladelementteorin varit ett användbart verktyg i händerna på erfarna propellerdesigners. Med den kan en skicklig konstruktör som har kunskap om lämpliga empiriska faktorer konstruera propellrar som vanligtvis passar de huvudsakliga villkor som ställs på dem ganska väl genom att de absorberar motorkraften vid mycket nära rätt varvtal. De är dock inte nödvändigtvis de mest effektiva propellrarna för sitt syfte, för den enkla teorin är inte tillräckligt exakt för att visa små skillnader i effektivitet på grund av förändringar i stigningsfördelning, planformer, etc.

Exempel

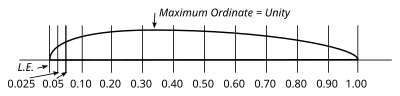
Fig 6. Ordinat för standardpropellersektion baserad på RAF-6.

Vid val av en propeller att analysera är det önskvärt att dess aerodynamiska egenskaper är kända så att noggrannheten hos de beräknade resultaten kan kontrolleras. Det är också önskvärt att analysen görs av en propeller som arbetar med en relativt låg spetshastighet för att vara fri från alla effekter av kompressibilitet och att den löper fri från kroppsstörningar. De enda propellertesterna som uppfyller alla dessa villkor är tester av modellpropellrar i vindtunnel. Vi ska därför som exempel ta centralpropellern eller huvudpropellern i en serie modell träpropellrar av standard marinform, testad av Dr. WF Durand vid Stanford University . Detta är en tvåbladig propeller på 3 fot i diameter, med en enhetlig geometrisk stigning på 2,1 fot (eller ett förhållande mellan stigning och diameter på 0,7). Bladen har standardpropellersektioner baserade på RAF-6-profilen (Fig. 6), och bladbredderna, tjockleken och vinklarna är de som anges i den första delen av Tabell I. I vår analys ska vi betrakta propellern som att den går framåt med en hastighet på 40 mph och vridning med en hastighet av 1 800 rpm

Fig 7. Två plana sektioner vända mot varandra.

För sektionen vid 75 % av spetsradien är radien 1,125 fot, bladets bredd är 0,198 fot, tjockleksförhållandet är 0,107, den nedre cambern är noll och bladvinkeln β är 16,6 ° .

Framhastigheten

{\begin{aligned}V&=40\ \mathrm {mph} \\&={\frac {40\times 88}{60}}\\&=58.65\ {\text{ft./sek .}},\end{aligned}}

Fig 8. Korrigering av lyftkoefficient för den konvexa nedre kammaren. (OBS: För en sektion med nedre kammare,

{\textstyle C_{L}=C_{L(flatface)}-\Delta C_{L }}

)

och

{\begin{aligned}n&={\frac {1800}{60}}\\&=30\ {\text{rps}}\end{aligned}}

Banvinkeln

{\begin{aligned}\phi &=\arctan {\frac {V}{2\pi rn}} \\&=\arctan {\frac {58.65}{2\pi \times 1.125\times 30}}\\&=15.5^{\circ }\end{aligned}}

Anfallsvinkeln är därför

{\begin{aligned}\alpha &=\beta -\phi \\&=16,6^{\circ }-15,5^{\circ }\ \&=1.1^{\circ }\\\end{aligned}}

CL _. 7, för en plan sektion med tjockleksförhållande 0,107 vid en anfallsvinkel av 1,1°, y = 3,0°, och, från fig. 9, = 0,425. (För sektioner som har nedre camber CL ₎ korrigeras i enlighet med förhållandet som anges i fig. 8, och γ ges samma värde som för en platt sektion som endast har den övre camberen.

Fig 9. Kurvor för gradering av dragkraft och vridmoment.

Sedan

{\begin{aligned}K&={\frac {C_{L}b}{\sin ^{2 }\phi \cos \gamma }}\\&={\frac {0.425\times 0.198}{0.2672^{2}\times 0.999}}\\&=1.180,\end{aligned}}

och,

{\begin{aligned}T_{C}&=K\cos(\phi +\gamma )\\&=1.180\times \cos 18.5^{\circ }\\&=1.119.\\\end {Justerat}}

Också,

{\begin{aligned}Q_{C}&=vK_{r}\sin(\phi +\gamma )\\&=1.180\times 1.125\times \sin 18.5^{\circ }\\&= 1.421.\end{aligned}}

Beräkningarna av Tc _, och Qc för sex representativa element av propellern ges i _. Qc är plottade mot radien _{lämplig tabellform i tabell I} och värdena för Tc _{i fig} och 9. Kurvorna som ritas genom dessa punkter är kallas ibland för vridmomentgraderingskurvorna. Ytorna under kurvan representerar

\int _{0}^{R}T_{c}dr

och

\int _{0}^{R}Q_{c}dr,

dessa är uttrycken för den totala dragkraften och vridmomentet per blad per enhet av dynamiskt tryck på grund av frammatningshastigheten. Områdena kan hittas med hjälp av en planimeter, varvid man naturligtvis tar rätt hänsyn till värdeskalorna, eller så kan integrationen utföras ungefär (men med tillfredsställande noggrannhet) med hjälp av Simpsons regel .

När man använder Simpsons regel delas radien i ett jämnt antal lika delar, till exempel tio. Ordinatan vid varje division kan sedan hittas från graderingskurvan. Om de ursprungliga bladelementen delar upp bladet i ett jämnt antal lika delar är det inte nödvändigt att plotta graderingskurvorna, men kurvorna är fördelaktiga genom att de grafiskt visar fördelningen av dragkraft och vridmoment längs bladet. De ger också en kontroll på beräkningarna, för felaktiga punkter kommer vanligtvis inte att bilda en rättvis kurva.

Tabell I. — Beräkningar för propelleranalys med enkel bladelementteori
D = 3,0 fot. p = 2,1 fot.	Hastighet framåt = 40 mph = 58,65 fot/sek. Rotationshastighet = 1 800 rpm = 30 rps
$r / R$	0,15	0,30	0,45	0,60	0,75	0,90
r (ft.)	0,225	0,450	0,675	0,900	1,125	1,350
b (ft.)	0,225	0,236	0,250	0,236	0,198	0,135
h _v /b	0,190	0,200	0,167	0,133	0,107	0,090
h _l /b	0,180	0,058	0,007	000	000	000
$β$ (grader)	56,1	36,6	26.4	20.4	16.6	13.9
$2 πrn$	42,3	84,7	127,1	169,6	212,0	254,0
${\textstyle \tan \phi ={\frac {V}{2\pi rn}}}$	1,389	0,693	0,461	0,346	0,277	0,231
$Φ$ (grader)	54,2	34,7	24.7	19.1	15.5	13,0
$\alpha =\beta -\phi \ \mathrm {(deg.)}$	1.9	1.9	1.7	1.3	1.1	0,9
$γ$ (grader)	3.9	4.1	3.6	3.3	3.0	3.0
$\cos \gamma$	0,998	0,997	0,998	0,998	0,999	0,999
C _L	0,084	0,445	0,588	0,514	0,425	0,356
$synd Φ$	0,8111	0,5693	0,4179	0,3272	0,2672	0,2250
${\textstyle K={\frac {C_{L}b}{\cos \gamma \sin ^{2}\phi }}}$	0,0288	0,325	0,843	1,135	1,180	0,949
$Φ+ γ$ (grader)	58,1	38,8	28.3	22.4	18.5	16,0
$cos(γ +Φ)$	0,5280	0,7793	0,8805	0,9245	0,9483	0,9613
${\textstyle T_{c}=K\cos(\gamma +\phi )}$	0,0152	0,253	0,742	1.050	1,119	0,912
$sin(γ +Φ)$	0,8490	0,6266	0,4741	0,3811	0,3173	0,2756
${\textstil Q_{c}=Kr\sin(\gamma +\phi )}$	0,0055	0,0916	0,270	0,389	0,421	0,353

Om abskissorna betecknas med r och ordinaterna vid de olika divisionerna med y ₁ , y ₂ , ..., y ₁₁ , blir arean med tio lika stora delar enligt Simpsons regel

\int _{0}^{R}F(r)\,dr={\frac {\Delta r}{3}}[y_{1}+2(y_{3}+y_{5} +y_{7}+y_{9})+4(y_{2}+y_{4}+y_{6}+y_{8}+y_{10})+y_{11}].

Arean under dragkraftsgraderingskurvan i vårt exempel är därför

skärm {\_int

och på liknande sätt

\int _{0}^{R}Q_{c}\,dr=0.340.

Ovanstående integrationer har också gjorts med hjälp av en planimeter, och medelresultaten från fem försök överensstämmer med dem som erhållits med Simpsons regel inom en fjärdedel av en procent.

Propellerns dragkraft i standardluft är

{\begin{aligned}T&={\frac {1}{2}}V^{2}B\int _{0}^{R}T_{c}dr\\&={\frac {1}{2}}\times 0,002378\times 58,65^{2}\times 2\times 0,9075\\&=7,42\ \mathrm {lb.} ,\end{aligned}}

och vridmomentet är

{\begin{aligned}Q&={\frac {1}{2}}\rho V^{2}B\int _{0}^{R}Q_{c}dr\\&={\ frac {1}{2}}\ gånger 0,002378\ gånger 58,65^{2}\ gånger 2\ gånger 0,340\\&=2,78\ \mathrm {lb.ft.} \end{aligned}}

Effekten som absorberas av propellern är

{\begin{aligned}P&=2\pi nQ\\&=2\times \pi \times 30\times 2.78\\&=524\ \mathrm {ft.lb./\ sek} .\end {Justerat}}

eller

{\begin{aligned}HP&={\frac {524}{550}}\\&=0,953,\end{aligned}}

och effektiviteten är

{\begin{aligned}\eta &={\frac {TV}{2\pi nQ}}\\&={\frac {7.42\times 58.65}{524}}\\&=0.830.\ end{aligned}}

Den ovan beräknade prestandan jämförs med den som uppmätts i vindtunneln enligt följande:

	Beräknad	Modelltest
Effektupptagen, hästkrafter	0,953	1,073
Drivkraft, pund	7,42	7,77
Effektivitet	0,830	0,771

Fig 10. - ( Från R. och M. 681. ) Förklaring: • Direkt mätning av krafter på en aerofoil med bildförhållande 6 med fyrkantiga ändar; o Beräknat från tryckfördelningen över mediansektionen av flygplanet med bildförhållande 6; x Beräknat från tryckfördelningen över sektion C av en aerofoil formad som ett luftskruvblad men utan vridning

Effekten beräknad av den enkla bladelementteorin är i detta fall över 11 % för låg, dragkraften är ca 5 % låg och verkningsgraden är ca 8 % hög. Naturligtvis skulle en annorlunda beräknad prestanda ha erhållits om propellersektionsegenskaper från tester på samma serie bärytor i en annan vindtunnel hade använts, men tunneltesterna med variabel densitet är förmodligen de mest tillförlitliga av alla.

Viss ljus kan kastas över avvikelsen mellan den beräknade och observerade prestandan genom att återigen hänvisa till tryckfördelningstesterna på en modellpropeller. I dessa tester mättes tryckfördelningen över flera sektioner av ett propellerblad medan propellern kördes i en vindtunnel, och de tre följande uppsättningarna av tester gjordes på motsvarande bärytor:

Standardkrafttester på bärytor med bildförhållande 6.
Tester av tryckfördelningen på mediandelen av ovanstående bärytor med bildförhållande 6.
Tester av tryckfördelningen över en speciell bäryta gjorda i form av ett blad på propellern, men utan vridning, trycket mäts vid samma sektioner som i propellerbladet.

Resultaten av dessa tre uppsättningar av bärytetest visas för sektionen vid tre fjärdedelar av spetsradien i fig. 10, som har hämtats från rapporten. Det kommer att märkas att koefficienterna för den resulterande kraften CR överensstämmer ganska väl för mediansektionen av vingprofilen med bildförhållande 6 och motsvarande sektion av _den speciella propellerbladsvingytan, men att den resulterande kraftkoefficienten för hela bärytan i bildförhållandet 6 är betydligt lägre. Det är därför naturligt att den beräknade dragkraften och effekten för en propeller är för låg när den baseras på bärytans egenskaper för bildförhållande 6.

Ändringar

Många modifieringar av den enkla bladelementteorin har föreslagits för att göra den mer komplett och förbättra dess noggrannhet. De flesta av dessa modifierade teorier försöker ta hänsyn till bladinterferensen, och i vissa av dem görs även försök att eliminera felaktigheten på grund av användningen av bärytedata från tester på vingar med ett ändligt bildförhållande, såsom 6. Den första modifieringen som skulle göras hade karaktären av en kombination av den enkla Drzewiecki-teorin med Froudes momentumteorin.

Diagram

Standardpropellersektioner baserade på RAF-6 Infinite bildförhållande.
Fig 11.
Fig 12.
Bild 13.
Bild 14.

Tillskrivning

Den här artikeln innehåller text från denna källa, som är allmän egendom : Weick, Fred Ernest (1899). Flygplanspropellerdesign . New York, McGraw-Hill Book Company, inc.

Se även

externa länkar

^ Froude, William (1878). Det elementära förhållandet mellan tonhöjd, slirning och framdrivningseffektivitet . Inst. Sjöarkitekter.
^ Detta faktum, som inte är allmänt känt i engelsktalande länder, uppmärksammades författaren av prof. FW Pawlowski vid University of Michigan. Drzewieckis första franska artikel om hans teori publicerades 1892. Han skrev i alla sju artiklar om flygplansframdrivning som presenterades för l'Academie des Sciences, l'Association Technique Maritime och Le Congrès International d'Architecture et de Construction Navale, som hölls den 15 juli 1900. Han skrev äntligen en bok som sammanfattar allt hans arbete som heter "Théorie Générale de l'Hé1ice Propulsive", publicerad 1920 av Gauthier-Villars i Paris.
^ Drzewiecki föreslog att bärytans egenskaper kunde erhållas från tester på speciella propellrar.
^ Glauert, H (1926). Aerofoil and Airscrew Theory . Cambridge University Press.
^ CNH, lås; Bateman, H.; Townend, HCH (1924). Experiment för att verifiera oberoendet av elementen i ett luftskruvsblad . Brittiska R. och M. 953.
^ ^a ^b Fage, A.; Howard, RG (1921). En övervägande av luftskruvsteorin i ljuset av data som härrör från en experimentell undersökning av tryckfördelningen över hela ytan av ett luftskruvsblad, och även över bärytor med lämpliga former . Brittiska R. och M. 681.
^ En analys av familjen av luftskruvar med hjälp av virvelteorin och mätningar av totalt huvud, av CNH Lock och H. Bateman, brittiska R. och M. 892, 1923.
^ Jämförelse av modellpropellertester med aerofoilteori, av William F. Durand och EP Lesley, NACA .TR 196, 1924.
^ Durand, WF (1926). Tester på tretton modellpropellrar av marintyp . NACA .TR 237. propeller modell C.

[1] Froude, William (1878). Det elementära förhållandet mellan tonhöjd, slirning och framdrivningseffektivitet . Inst. Sjöarkitekter.

[2] Detta faktum, som inte är allmänt känt i engelsktalande länder, uppmärksammades författaren av prof. FW Pawlowski vid University of Michigan. Drzewieckis första franska artikel om hans teori publicerades 1892. Han skrev i alla sju artiklar om flygplansframdrivning som presenterades för l'Academie des Sciences, l'Association Technique Maritime och Le Congrès International d'Architecture et de Construction Navale, som hölls den 15 juli 1900. Han skrev äntligen en bok som sammanfattar allt hans arbete som heter "Théorie Générale de l'Hé1ice Propulsive", publicerad 1920 av Gauthier-Villars i Paris.

[3] Drzewiecki föreslog att bärytans egenskaper kunde erhållas från tester på speciella propellrar.

[4] Glauert, H (1926). Aerofoil and Airscrew Theory . Cambridge University Press.

[5] CNH, lås; Bateman, H.; Townend, HCH (1924). Experiment för att verifiera oberoendet av elementen i ett luftskruvsblad . Brittiska R. och M. 953.

[:0-6] Fage, A.; Howard, RG (1921). En övervägande av luftskruvsteorin i ljuset av data som härrör från en experimentell undersökning av tryckfördelningen över hela ytan av ett luftskruvsblad, och även över bärytor med lämpliga former . Brittiska R. och M. 681.

[7] En analys av familjen av luftskruvar med hjälp av virvelteorin och mätningar av totalt huvud, av CNH Lock och H. Bateman, brittiska R. och M. 892, 1923.

[8] Jämförelse av modellpropellertester med aerofoilteori, av William F. Durand och EP Lesley, NACA .TR 196, 1924.

[9] Durand, WF (1926). Tester på tretton modellpropellrar av marintyp . NACA .TR 237. propeller modell C.