Autowave

Autovågor är självbärande icke-linjära vågor i aktiva medier (dvs de som tillhandahåller distribuerade energikällor). Termen används generellt i processer där vågorna bär relativt låg energi, vilket är nödvändigt för synkronisering eller omkoppling av det aktiva mediet.

Introduktion

Relevans och betydelse

Autovågor (AW) är distribuerade analoger till den självsvängning som observeras i punktvisa system. Exempel på dem är förbränningsvågor, nervimpulser, vågor av distributionstunnelövergång (i halvledare), etc. Autovågsprocesser (AWP) ligger till grund för majoriteten av processerna för hantering och informationsöverföring i biologiska system. (...) En intressant egenskap hos de aktiva medierna är att autovågsstrukturer (AWS) kan förekomma i dem. (...) Vikten av detta arbete är som följer 1. Både AW och AWS kan förekomma i system av vilken fysisk natur som helst, vars dynamik beskrivs av ekvationerna (1) . 2. Detta är en ny typ av dynamiska processer som ger upphov till den makroskopiska linjära skalan genom lokala interaktioner, som var och en inte har en linjär skala 3. AWS ger grunden för morfogenesen i levande organismer (dvs i biologiska system). 4. En uppkomst av AWS är en ny mekanism för turbulens i aktiva miljöer.

Klicka på " visa " för att se originaltexten ( på ryska)

Автоволны (АВ) являются распределёнными аналогами автоколебаний in сосредоточенных системах. Их примерами являются волны горения, нервные импульсы, волны распределения туннельных перехолдов (в похоления) Автоволновые процессы (АВП) лежат в основе большинства процессов управления och передачи информацолхив ским. (...) Интересной особенностью активных сред является то, что в них могут возникать автоволновных сред является то, что в них могут возникать автоволновных сред является то, что в них могут возникать автоволновть автоволновтые (Асть автоволновтые (...) ВС определяется следующим: 1. АВ и АВС могут осуществляться в системах любой физической прика ается уравнениями вида (1) . 2. Это новый тип динамических процессов , порождающих макроскопический линейный масштаб залосчё каждое из которых линейным масштабом не обладает. 3. АВС являются основой морфогенеза в биологических системах. 4. Возникновение АВС — новый механизм турбулентности в активных средах.

— (1981),

1980 blev de sovjetiska forskarna GR Ivanitsky, VI Krinsky, AN Zaikin, AM Zhabotinsky , BP Belousov vinnare av Sovjetunionens högsta statliga pris, Leninpriset " för upptäckten av en ny klass av autovågsprocesser och studien av dem i störning av stabiliteten hos de distribuerade exciterbara systemen ."

En kort historia av autowave-forskningar

Den första som aktivt studerade självsvängningarna var akademikern AA Andronov , och termen " autosvängningar " i rysk terminologi introducerades av AA Andronov 1928. Hans anhängare från Lobatsjovskij-universitetet bidrog ytterligare i hög grad till utvecklingen av autovågsteorin .

De enklaste autovågsekvationerna som beskriver förbränningsprocesser har studerats av AN Kolmogorov , IE Petrovsky, NS Piskunov 1937., såväl som av Ya.B. Zel'dovich och DA Frank-Kamenetsky 1938.

Den klassiska axiomatiska modellen med autovågor i myokardiet publicerades 1946 av Norbert Wiener och Arturo Rosenblueth .

Under 1970-80 koncentrerades stora ansträngningar för att studera autovågor till Institutet för biologisk fysik vid USSR Academy of Sciences, beläget i förortsstaden Pushchino , nära Moskva. Det var här, under ledning av VIKrinsky, så världsberömda nu experter inom området för autovågsforskning som AVPanfilov, IREfimov, RRAliev, KI Agladze, OAMornev, MATsyganov utbildades och utbildades. VVBiktashev, Yu.E. Elkin, AV Moskalenko fick sin erfarenhet av autovågsteorin också i Pushchino, i det angränsande Institute of Mathematical Problems of Biology , under ledning av EEShnoll.

Termen "autovågsprocesser" för alla dessa (och andra) fenomen myntades av USSR-fysikern RV Khokhlov. Det finns bestämda och viktiga relationer mellan dessa autovågor och idéer från synergetik och självorganisering.

— VA Vasiliev etc. (1987),

Termen " autovågor " föreslogs förmodligen på analogi av tidigare " autosvängningar ".

Nästan omedelbart efter Sovjetunionens upplösning lämnade många av dessa ryska vetenskapsmän sitt hemland för att arbeta på utländska institutioner, där de fortfarande fortsätter sina studier av autovågor. I synnerhet utvecklar EREfimov teorin om virtuell elektrod , som beskriver vissa effekter som uppstår under defibrillering .

Bland andra framstående forskare, som är engagerade i dessa undersökningar, finns AN Zaikin och EEShnoll (autovågor och bifurkationsminne i blodkoagulationssystemet); A.Yu. Loskutov (allmän autovågteori såväl som dynamiskt kaos i autovågor); VG Yakhno (allmän autovågteori samt kopplingar mellan autovågor och tankeprocess); KI Agladze (autovågor i kemiska medier); VNBiktashev (allmän autovågteori såväl som olika sorters autovågsdrift); OAMornev (allmän autovågsteori); MATsyganov (autovågens roll i befolkningsdynamik); Yu.E. Elkin, AV Moskalenko, ( bifurkationsminne i en modell av hjärtvävnad).

En stor roll i studiet av autowave-modeller av hjärtvävnad tillhör Denis Noble och medlemmar av hans team från University of Oxford .

De grundläggande definitionerna

En av de första definitionerna av autovågor var följande:

Det är nu accepterat att betrakta en autovåg som en självuppehållande vågprocess i en icke-jämviktsmiljö som förblir oförändrad för tillräckligt små förändringar i både initial- och randvillkor. (...) Matematiska apparater för att beskriva autovågor är ofta ekvationer av diffusionstyp med en aktiv olinjäritet .

Klicka på " visa " för att se originaltexten ( på ryska)

Под автоволнами принято сейчас понимать самоподдерживающийся волновой процесс в неравновесной сревновесной сревноволнами при достаточно малых изменениях как начальных, так и граничных условий. (...) Математическим аппаратом для описания автоволн чаще всего служат уравнения диффузионого типанин с.

— (1981),

Till skillnad från linjära vågor - såsom ljudvågor, elektromagnetiska vågor och annat, som är inneboende i konservativa system och matematiskt beskrivna av linjära andra ordningens hyperboliska ekvationer ( vågekvationer ), - kan dynamiken hos en autovåg i termer av differentialekvationer beskrivas med paraboliska ekvationer med olinjär gratis medlem av en speciell form .

Den konkreta formen av den fria medlemmen ${\vec {f}}({\vec {u}})$ är extremt viktig, eftersom:

...alla vågprocesser som genereras av den olinjära dynamiken i ett punktsystem ${\dot {\vec {u}}}={\vec {f}}({\ vec {u}})$ , som är en självsvängande eller potentiellt självsvängande.

Klicka på " visa " för att se originaltexten ( på ryska)

все волновые процессы порождаются динамикой нелинейной точечной системы ${\displaystyle= {\dot}c {\}c {\}c {\}c {\} {\} }$ , которая является автоколебательной или потенциально автоколебательной.

— (1981),

Vanligtvis har $f$ formen av $N$ -format beroende av $u$ . I denna mening är ekvationssystemet, känt som Aliev–Panfilov-modellen, ett mycket exotiskt exempel, eftersom $f(u)$ har en mycket komplex form av två som skär varandra paraboler, förutom mer korsade med två raka linjer, vilket resulterar i en mer uttalad olinjär egenskaper hos denna modell.

Autowaves är ett exempel på en självuppehållande vågprocess i omfattande olinjära system som innehåller distribuerade energikällor. Det är korrekt för enkla autovågor, att period, våglängd, utbredningshastighet, amplitud och vissa andra egenskaper hos en autovåg bestäms enbart av lokala egenskaper hos mediet. Men under 2000-talet började forskare upptäcka ett växande antal exempel på självvågslösningar när den "klassiska" principen kränks.

(Se även allmän information i litteraturen, till exempel i).

De enklaste exemplen

En växlingsvågfrontlösning för Fishers ekvation (se Reaktion-diffusion för detaljer).

Den enklaste modellen av autowave är en rang av domino som faller en efter en, om du tappar en yttersta (så kallad " dominoeffekt "). Detta är ett exempel på en växlingsvåg .

Som ett annat exempel på autovågor, föreställ dig att du står på en åker och sätter eld på gräset. Medan temperaturen är under tröskeln kommer gräset inte att ta eld. När tröskeltemperaturen (självantändningstemperatur) har uppnåtts börjar förbränningsprocessen , med frigöring av värme som är tillräcklig för att antända de närmaste områdena . Resultatet är att förbränningsfronten har formats, som sprider sig genom fältet. Man kan i sådana fall säga att autovåg uppstod, vilket är ett av resultaten av självorganisering i termodynamiska system utan jämvikt. Efter en tid ersätter nytt gräs det brända gräset och fältet får igen förmågan att antändas. Detta är ett exempel på en excitationsvåg .

Det finns en hel del andra naturliga föremål som också beaktas bland autovågsprocesser: oscillerande kemiska reaktioner i aktiva medier (t.ex. Belousov–Zhabotinsky-reaktionen ), spridningen av excitationspulser längs nervfibrer, vågkemisk signalering i kolonierna av vissa mikroorganismer , autovågor i ferroelektriska och halvledarfilmer , befolkningsvågor, spridning av epidemier och gener och många andra fenomen.

Nervimpulser, som fungerar som ett typiskt exempel på autovågor i ett aktivt medium med återhämtning, studerades så långt tillbaka som 1850 av Hermann von Helmholtz . Egenskaperna hos nervimpulser som är typiska för de enklaste självvågslösningarna (universell form och amplitud, oberoende av utgångsförhållandena och förintelse under kollisioner) konstaterades på 1920- och 1930-talen.

Schematisk beskrivning av en elektrofysiologisk registrering av en aktionspotential som visar de olika faserna som uppstår när vågen passerar en punkt på ett cellmembran .

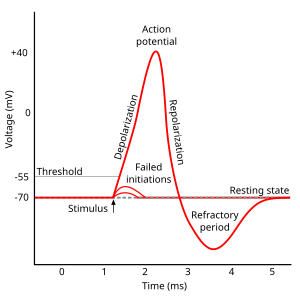
Tänk på ett aktivt 2D-medium som består av element, som var och en kan hittas i tre olika tillstånd: vila, excitation och eldfasthet . I frånvaro av yttre påverkan är element i vila. Som ett resultat av ett inflytande på det, när koncentrationen av aktivatorn når tröskeln, kommer elementet att växla till ett exciterat tillstånd och förvärva förmågan att excitera de närliggande elementen. En tid efter exciteringen växlar elementet till ett eldfast tillstånd, i vilket det inte kan exciteras. Sedan återgår elementet till sitt ursprungliga viloläge och får åter förmågan att förvandlas till ett upphetsat tillstånd.

Varje "klassisk" excitationsvåg rör sig i ett exciterbart medium utan dämpning och bibehåller sin form och amplitud konstant. När den passerar kompenseras energiförlusten ( förlusten ) helt av energitillförseln från elementen i det aktiva mediet. Den främre fronten av en autovåg (övergången från vila till ett tillstånd av excitation) är vanligtvis mycket liten: till exempel är förhållandet mellan den främre frontvaraktigheten och hela pulsens varaktighet för ett myokardprov cirka 1:330.

Unika möjligheter att studera autovågsprocesser i två- och tredimensionella aktiva medier med mycket olika kinetik ges med metoder för matematisk modellering med hjälp av datorer. För datorsimulering av autovågor använder man en generaliserad Wiener–Rosenblueth-modell, såväl som ett stort antal andra modeller, bland vilka en speciell plats upptas av FitzHugh–Nagumo-modellen (den enklaste modellen av ett aktivt medium, och dess olika versioner) och Hodgkin-Huxley-modellen (nervimpuls). Det finns också många autowave myokardmodeller: Beeler-Reuter-modellen, flera Noble-modeller (utvecklade av Denis Noble ), Aliev-Panfilov-modellen, Fenton-Karma-modellen, etc.

Grundläggande egenskaper för autovågor

Det bevisades också att de enklaste autovågsregimerna borde vara gemensamma för varje system av differentialekvationer av vilken komplexitet som helst som beskriver ett särskilt aktivt medium, eftersom ett sådant system kan förenklas till två differentialekvationer.

Huvudsakliga kända autowave-objekt

Först och främst bör vi lägga märke till att elementen i de aktiva medierna åtminstone kan vara av tre mycket olika typer; dessa är självspännande , exciterande och utlösande (eller bistabila ) regimer. Följaktligen finns det tre typer av homogena aktiva medier som består av dessa element.

Ett bistabilt element har två stabila stationära tillstånd, mellan vilka övergångar sker när yttre påverkan överskrider en viss tröskel. I media av sådana element växlingsvågor , som växlar mediet från ett av dess tillstånd till det andra. Till exempel är ett klassiskt fall av en sådan växlande autovåg - kanske det enklaste autovågsfenomenet - fallande dominobrickor (exemplet som redan ges). Ett annat enkelt exempel på ett bistabilt medium är brinnande papper: växlingsvågen fortplantar sig i form av en låga och växlar papper från normalt tillstånd till sin aska.

Ett exciterbart element har bara ett stabilt stationärt tillstånd. Extern påverkan över en tröskelnivå kan föra ett sådant element ut ur sitt stationära tillstånd och utföra en utveckling innan elementet återgår till sitt stationära tillstånd. Under sådan utveckling kan det aktiva elementet påverka de intilliggande elementen och i sin tur leda dem ut ur det stationära tillståndet också. Som ett resultat excitationsvågen i detta medium. Detta är den vanligaste formen av autovågor i biologiska medier, såsom nervvävnad eller myokardiet.

Ett självoscillerande element har inga stationära tillstånd och utför kontinuerligt stabila svängningar av någon fast form, amplitud och frekvens. Extern påverkan kan störa dessa svängningar. Efter lite avslappningstid, alla deras egenskaper förutom fasen tillbaka till sitt stabila värde, men fasen kan ändras. Som ett resultat fasvågorna i mediet för sådana element. Sådana fasvågor kan observeras i elektrogirlander eller i vissa kemiska medier. Ett exempel på ett självoscillerande medium är SA-noden i hjärtat, där excitationspulser uppstår spontant.

Det kan tydligt ses på fasporträttet av det grundläggande ekvationssystemet som beskriver det aktiva mediet (se fig.) att en signifikant skillnad mellan dessa tre typer av beteende hos ett aktivt medium orsakas av kvantiteten och positionen för dess singularpunkter . Formen på autovågor som observeras i verkligheten kan vara mycket lika varandra, och därför kan det vara svårt att bedöma typen av element endast genom formen av excitationspulsen.

Dessutom beror autovågsfenomen, som kan observeras och undersökas, mycket på geometriska och topologiska särdrag hos ett aktivt medium.

Endimensionella autovågor

Endimensionella fall inkluderar autovågsspridning i kabel och dess spridning i ringen, där det senare läget betraktas som ett begränsande fall av en roterande våg i tvådimensionellt aktivt medium, medan det första fallet betraktas som spridning av autovågen i ringen med noll krökning (dvs med en oändlig radie).

Tvådimensionella autovågor

Autowave-reverberator som finns i ovanstående tvåkomponents reaktion-diffusionssystem av Fitzhugh-Nagumo- typ.

Ett antal autovågskällor är kända i det tvådimensionella aktiva mediet. På ett sådant sätt särskiljs det åtminstone fem typer av återinträde, som löper runt ringen , spiralvåg , efterklang (dvs. tvådimensionell autovågvirvel ) och flimmer . Litteraturen identifierar två typer av källor för koncentriska autovågor i aktiva 2D-medier; dessa är pacemakers och ledande centra . Både de ledande centran och efterklangarna är intressanta, eftersom de inte är bundna till mediets struktur och kan dyka upp och försvinna i dess olika delar. Områden med ökad automatisering kan också vara ett exempel på en källa till autovågor. Tre olika typer av ökad automatisering är kända nu:

1. inducerad automatism
2. utlösa automatism med mekanismen för tidig postdepolarisering
3. utlösa automatism med mekanismen för sen postdepolarisering .

Dessutom om 2D

Se även detaljer i artikeln roterande autovågor, som kan visas som spiralvåg eller autovågsreverberator .

Fenomen med bifurkationsminne observerades i beteendet hos autovågsreverberatorn i Aliev-Panfilov-modellen.

Tredimensionella autovågor

3D.

Exempel på autovågsprocesser i naturen

Autovågor i kemiska lösningar

Ett exempel på en kemisk reaktion, som under vissa omständigheter kan producera autovåg, är Belousov-Zhabotinsky-reaktionen .

Autowave-modeller av biologiska vävnader

Autowave-modeller av nervfibrer

Huvudartikeln på sidan " Hodgkin–Huxley modell "

Autowave-modeller av myokardium

Den klassiska Wiener-Rosenblueth-modellen, som därför är utvecklad av Norbert Wiener och Arturo Rosenblueth .

Bland andra exempel är följande: FitxHue-Nagumo, modellen Beeler-Reuter.

Huvudartikeln är planerad att finnas på specialsidan "Autowave-modeller av myokardium"

Autovågor i blodkoagulationssystemet

Se referenser.

Befolkningen autowaves

Kollektiva amöbor Dictyostelium discoideum med tillräcklig tillgång lever som encelliga organismer . Men under svält kryper de ihop och bildar en flercellig organism , som senare ger sporer som kan överleva under ogynnsamma förhållanden. Det visade sig att amöbors rörelse styrs av distribution av något ämne, morfogen cAMP , i miljön. Sådana amöbaceller syntetiserar och ackumulerar molekylerna av cAMP och sedan kan de "släppa" denna reserv i miljön, om koncentrationen av cAMP i den ökar. Den frigjorda mängden cAMP diffunderar genom miljön och gör att följande cellamöbor "snäpper igång" genom att kasta ut sin del av morfogenen. Som ett resultat sprider sig en autovåg med hög koncentration av cAMP genom miljön. Efter vågens passage börjar de "urladdade" cellerna ackumulera en ny del av cAMP igen, på grund av syntesen, och efter ett tag kan de "snäppa till handling" igen. Alltså befolkningen i de kollektiva amöbor är ett typiskt exempel på det aktiva mediet .

Klicka på " visa " för att se originaltexten ( på ryska)

Коллективные амёбы Dictyostelium discoideum при наличие достаточного питания живут в виде одноклеточных организмов . Однако при голодании они сползаются и образуют Многоклеточный организм , который впоследствии даё ть неблагоприятные условия. Установлено , что движение амёб управляется распределением по среде некоторого вещества — морфогена цАММ Клетки амёб синтезируют и накапливают в себе молекулы цАМФ и способны «высвободитьвают» его запую если концентрация цАМФ в ней повысилась. Освободившееся количество цАМФ распространяется за счёт диффузии по среде и заставляет следивющ, « выбросив свою порцию морфогена. В результате по среде распространяется автоволна — повышенная концентрация цАМФ. После прохождения волны «разрядившиеся» клетки начинают вновь накапливать за счёт синтеза опреюцор по прошествии некоторого времени способны «срабатывать» вновь. Таким образом, популяция коллективных амёб служит типичным примером активной среды.

– Krinsky & Mikhailov, (1984)

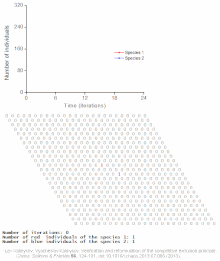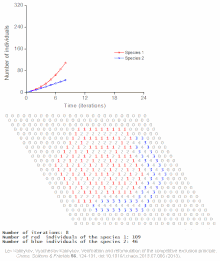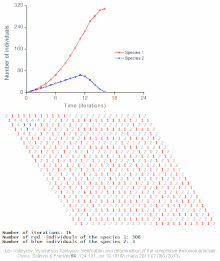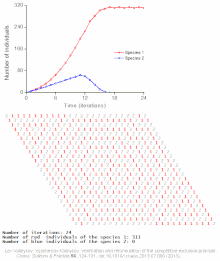
Exempel på individbaserade modeller av befolkningsautovågor

Logisk deterministisk individbaserad cellulär automatmodell av ett ekosystem med en art. Modellen visar en mekanism för S-formad befolkningstillväxt.

Logisk deterministisk individbaserad cellulär automatmodell av interspecifik konkurrens om en enda begränsad resurs. En mekanism för konkurrerande uteslutning av en art av en annan.

Se även

• Förlust
• Spännande medium
• Partiell differentialekvation
• Parabolisk partiell differentialekvation
• Reaktion-diffusionssystem
• Självsvängning
• Självorganisering
• Kardiofysik
• Refraktär period (fysiologi)
• Vinka
• ru:Нелинейная волна
• Stående våg
• Resonans
• Fashastighet

Anteckningar

• Böcker

• Papper

externa länkar

• Flera enkla klassiska modeller av autowaves (JS + WebGL), som kan köras direkt i din webbläsare; utvecklad av Evgeny Demidov.