Wiener–Araya-graf
| Wiener-Araya graf | |
|---|---|
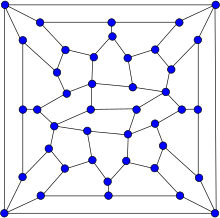 | |
| Vertices | 42 |
| Kanter | 67 |
| Radie | 5 |
| Diameter | 7 |
| Omkrets | 4 |
| Automorfismer | 2 |
| Kromatiskt nummer | 3 |
| Kromatiskt index | 4 |
| Egenskaper |
Hypohamiltonian Planar |
| Tabell över grafer och parametrar | |
Wiener –Araya-grafen är, i grafteorin , en graf på 42 hörn med 67 kanter. Den är hypohamiltonisk , vilket betyder att den inte själv har en hamiltonsk cykel utan varje graf som bildas genom att ta bort en enda vertex från den är hamiltonsk . Den är också plan .
Historia
Hypohamiltoniska grafer studerades först av Sousselier i Problèmes plaisants et délectables (1963). 1967 byggde Lindgren en oändlig sekvens av hypohamiltonska grafer. Han citerade först Gaudin, Herz och Rossi, sedan Busacker och Saaty som pionjärer i detta ämne.
Från början är den minsta hypohamiltonska grafen känd: Petersen-grafen . Jakten på den minsta plana hypohamiltonska grafen fortsätter dock. Denna fråga ställdes först av Václav Chvátal 1973. Det första kandidatsvaret gavs 1976 av Carsten Thomassen , som visade en konstruktion med 105 hörn, 105-Thomassen-grafen. 1979 förbättrade Hatzel detta resultat med en plan hypohamiltonisk graf på 57 hörn: Hatzel-grafen. Denna gräns sänktes 2007 av 48-Zamfirescu-grafen.
År 2009 blev en graf byggd av Gábor Wiener och Makoto Araya (med sina 42 hörn) den minsta plana hypohamiltonska grafen man känner till. I sin artikel antog Wiener och Araya att deras grafer är optimala och hävdar att dess ordning ( 42 ) verkar vara svaret på The Ultimate Question of Life, the Universe and Everything from The Hitchhiker's Guide to the Galaxy , en Douglas Adams- roman.