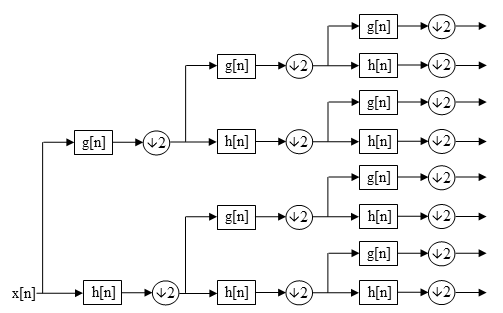
Wavelet-paketnedbrytning

Ursprungligen känd som optimal subband tree strukturing (SB-TS), även kallad wavelet packet decomposition (WPD) (ibland känd som bara wavelet-paket eller subband tree ), är en wavelet- transform där den diskreta (samplade) signalen passerar genom mer filter än den diskreta wavelet-transformen (DWT).

Introduktion

passera de tidigare waveletapproximationskoefficienterna ( cAj _. ) genom diskreta låg- och högpass- kvadraturspegelfilter I WPD sönderdelas emellertid både detalj ( , _cD j ₍ i 1-D-fallet), ( i 2-D _cHj , _- cVj cDj fallet)) och approximationskoefficienterna för att skapa det fullständiga binära trädet.

Wavelet-paketnedbrytning över 3 nivåer. g[n] är lågpassapproximationskoefficienterna, h[n] är högpassdetaljkoefficienterna.

För n nivåer av nedbrytning producerar WPD 2 ⁿ olika uppsättningar av koefficienter (eller noder) i motsats till ( n + 1) uppsättningar för DWT. Men på grund av nedsamplingsprocessen är det totala antalet koefficienter fortfarande detsamma och det finns ingen redundans.

Ur kompressionssynpunkt kan det hända att standardwavelettransformen inte ger det bästa resultatet, eftersom den är begränsad till waveletbaser som ökar med en potens av två mot de låga frekvenserna. Det kan vara så att en annan kombination av baser producerar en mer önskvärd representation för en viss signal. Det finns flera algoritmer för strukturering av delbandsträd som hittar en uppsättning optimala baser som ger den mest önskvärda representationen av data i förhållande till en viss kostnadsfunktion ( entropi , energikomprimering, etc.). Det fanns relevanta studier inom signalbehandlings- och kommunikationsfält för att ta itu med urvalet av delbandsträd (ortogonal basis) av olika slag, t.ex. regelbundna, dyadiska, oregelbundna, med avseende på prestandamått av intresse inklusive energikomprimering (entropi), subbandskorrelationer och andra .

Diskret wavelet-transformteori (kontinuerlig i tidsvariabeln) erbjuder en approximation för att transformera diskreta (samplade) signaler. Däremot möjliggör diskret-tid subband transformation teorin en perfekt representation av redan samplade signaler.

Galleri

Daubechies D12-paketfunktioner
Deras Fourier-spektra

Ansökningar

Wavelet-paket användes framgångsrikt i preklinisk diagnos.

^ ^a ^b Coifman RR & Wickerhauser MV, 1992. Entropi-baserade algoritmer för bästa basval , IEEE-transaktioner på informationsteori, 38(2).
^ ^a ^b ^c A. N. Akansu och Y. Liu, på signalnedbrytningstekniker , (inbjudet papper), Optisk iscensättande tidskrift, specialutgåva visuell kommunikation och bildbearbetning, vol. 30, s. 912–920, juli 1991.
^ Daubechies, I. (1992), Tio föreläsningar om wavelets, SIAM.
^ ^a ^b H. Caglar, Y. Liu och AN Akansu, statistiskt optimerad PR-QMF-design, Proc. SPIE Visual Communications and Image Processing, vol. 1605, s. 86–94, 1991.
^ ^a ^b ^c A. N. Akansu och RA Haddad, Multiresolution Signalupplösning: Transformers, Subbands och Wavelets . Boston, MA: Academic Press, ISBN 978-0-12-047141-6 , 1992.
^ ^a ^b A. Benyassine och AN Akansu, prestandaanalys och optimal strukturering av underkanaler för diskreta multitonsändtagare, Proc. IEEE International Symposium on Circuits and Systems (ISCAS), s. 1456–1459, april 1995.
^ ^a ^b M. V. Tazebay och AN Akansu, adaptiva subbandstransformers i tidsfrekvensexcisörer för DSSS-kommunikationssystem, IEEE Trans. Signal Process., vol. 43, s. 2776–2782, nov. 1995.
^ AN Akansu, WA Serdijn och IW Selesnick, Wavelet-omvandlingar i signalbehandling: En recension av framväxande applikationer , fysisk kommunikation, Elsevier, vol. 3, nummer 1, s. 1–18, mars 2010.
^ Zhang, Y.; Dong, Z. (2015). "Preklinisk diagnos av magnetisk resonans (MR) hjärnbilder via diskret Wavelet Packet Transform med Tsallis Entropy och Generalized Eigenvalue Proximal Support Vector Machine (GEPSVM)" . Entropi . 17 (4): 1795–1813. Bibcode : 2015Entrp..17.1795Z . doi : 10.3390/e17041795 .

externa länkar

En implementering av wavelet-paketnedbrytning kan hittas i MATLAB wavelet toolbox .
En implementering för R finns i wavethresh-paketet .
En illustration och implementering av wavelet-paket tillsammans med dess kod i C++ finns på: Ian Kaplan (mars 2002). "The Wavelet Packet Transform" . Bearcave .
JWave : En implementering i Java för 1-D och 2-D wavelet-paket som använder Haar , Daubechies , Coiflet och Legendre wavelets.

[coifman1992-1] Coifman RR & Wickerhauser MV, 1992. Entropi-baserade algoritmer för bästa basval , IEEE-transaktioner på informationsteori, 38(2).

[akansu1991-2] A. N. Akansu och Y. Liu, på signalnedbrytningstekniker , (inbjudet papper), Optisk iscensättande tidskrift, specialutgåva visuell kommunikation och bildbearbetning, vol. 30, s. 912–920, juli 1991.

[Daub-3] Daubechies, I. (1992), Tio föreläsningar om wavelets, SIAM.

[caglar1991-4] H. Caglar, Y. Liu och AN Akansu, statistiskt optimerad PR-QMF-design, Proc. SPIE Visual Communications and Image Processing, vol. 1605, s. 86–94, 1991.

[akansu1992-5] A. N. Akansu och RA Haddad, Multiresolution Signalupplösning: Transformers, Subbands och Wavelets . Boston, MA: Academic Press, ISBN 978-0-12-047141-6 , 1992.

[benyassine1995-6] A. Benyassine och AN Akansu, prestandaanalys och optimal strukturering av underkanaler för diskreta multitonsändtagare, Proc. IEEE International Symposium on Circuits and Systems (ISCAS), s. 1456–1459, april 1995.

[akansu1995-7] M. V. Tazebay och AN Akansu, adaptiva subbandstransformers i tidsfrekvensexcisörer för DSSS-kommunikationssystem, IEEE Trans. Signal Process., vol. 43, s. 2776–2782, nov. 1995.

[8] AN Akansu, WA Serdijn och IW Selesnick, Wavelet-omvandlingar i signalbehandling: En recension av framväxande applikationer , fysisk kommunikation, Elsevier, vol. 3, nummer 1, s. 1–18, mars 2010.

[9] Zhang, Y.; Dong, Z. (2015). "Preklinisk diagnos av magnetisk resonans (MR) hjärnbilder via diskret Wavelet Packet Transform med Tsallis Entropy och Generalized Eigenvalue Proximal Support Vector Machine (GEPSVM)" . Entropi . 17 (4): 1795–1813. Bibcode : 2015Entrp..17.1795Z . doi : 10.3390/e17041795 .