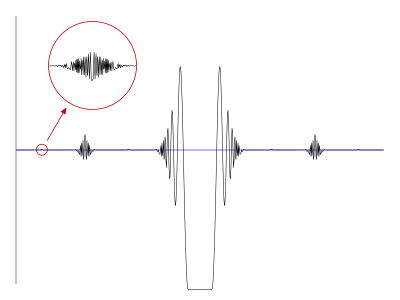
Volterras funktion

De tre första stegen i uppbyggnaden av Volterras funktion.

Inom matematik är Volterras funktion , uppkallad efter Vito Volterra , en verkligt värderad funktion V definierad på den reella linjen R med följande märkliga kombination av egenskaper:

• V är differentierbar överallt
• Derivatan V ′ är gränsad överallt
• Derivaten är inte Riemann-integrerbar .

Definition och konstruktion

₀₀ Funktionen definieras genom att använda Smith–Volterra–Cantor-uppsättningen och "kopior" av funktionen definierad av $f(x)=x^{2 }\sin(1/x)$ för $x\neq 0$ och $f(0)=0$ . Konstruktionen av V börjar med att bestämma det största värdet av x i intervallet [0, 1/8] för vilket f ′( x ) = 0. När detta värde (säg x ) har bestämts, utöka funktionen till höger med en konstant värde på f ( x ) till och med punkten 1/8. När detta är gjort kan en spegelbild av funktionen skapas med början vid punkten 1/4 och sträcker sig nedåt mot 0. Denna funktion kommer att definieras som 0 utanför intervallet [0, 1/4]. Vi översätter sedan denna funktion till intervallet [3/8, 5/8] så att den resulterande funktionen, som vi kallar f ₁ , endast är lik noll på mittintervallet av komplementet till Smith–Volterra–Cantor-mängden. För att konstruera f ₂ , betraktas f ′ sedan på det mindre intervallet [0,1/32], trunkerat på den sista platsen där derivatan är noll, utökad och speglad på samma sätt som tidigare, och två översatta kopior av den resulterande funktionen läggs till f ₁ för att producera funktionen f ₂ . Volterras funktion resulterar sedan i att denna procedur upprepas för varje intervall som tas bort i konstruktionen av Smith–Volterra–Cantor-setet; med andra ord, funktionen V är gränsen för sekvensen av funktioner f ₁ , f ₂ , ...

Ytterligare fastigheter

Volterras funktion är differentierbar överallt precis som f (enligt definitionen ovan) är. Man kan visa att f ′( x ) = 2 x sin(1/ x ) - cos(1/ x ) för x ≠ 0, vilket betyder att det i vilken omgivning som helst av noll finns punkter där f ′ tar värdena 1 och − 1. Det finns alltså punkter där V ′ tar värdena 1 och −1 i varje grannskap av var och en av ändpunkterna för intervall som tas bort i konstruktionen av Smith–Volterra–Cantor-uppsättningen S . Faktum är V ′ är diskontinuerlig vid varje punkt av S , även om V själv är differentierbar vid varje punkt av S , med derivata 0. V ′ är dock kontinuerlig på varje intervall som tas bort i konstruktionen av S , så uppsättningen av diskontinuiteter av V ′ är lika med S .

Eftersom Smith–Volterra–Cantor-uppsättningen S har ett positivt Lebesgue-mått , betyder detta att V ′ är diskontinuerligt på en uppsättning av positivt mått. Enligt Lebesgues kriterium för Riemann-integrerbarhet är V ′ inte Riemann-integrerbar . Om man skulle upprepa konstruktionen av Volterras funktion med det vanliga måttet-0 Kantormängd C i stället för den "fetta" (positivt mått) Cantormängden S , skulle man få en funktion med många liknande egenskaper, men derivatan skulle då vara diskontinuerlig på mått-0-mängden C istället för den positiva måttuppsättningen S , och så skulle den resulterande funktionen ha en Riemann-integrerbar derivata.

Se även

• Fundamental sats för kalkyl

externa länkar

• Wrestling with the Fundamental Theorem of Calculus: Volterra's function , föredrag av David Marius Bressoud
• Volterras exempel på en derivat som inte är integrerad ( PPT ), tal av David Marius Bressoud