Typ-2 fuzzy set och system
Typ-2 fuzzy set och system generaliserar standard Typ-1 fuzzy set och system så att mer osäkerhet kan hanteras. Från början av fuzzy uppsättningar framfördes kritik mot att medlemskapsfunktionen i en typ-1 fuzzy set inte har någon osäkerhet förknippad med sig, något som verkar motsäga ordet fuzzy , eftersom det ordet har innebörden av mycket osäkerhet . Så, vad gör man när det råder osäkerhet om värdet av medlemsfunktionen? Svaret på denna fråga gavs 1975 av uppfinnaren av fuzzy set, Lotfi A. Zadeh , när han föreslog mer sofistikerade typer av fuzzy set, av vilka den första han kallade en "typ-2 fuzzy set". En fuzzy-uppsättning av typ 2 låter oss införliva osäkerhet om medlemskapsfunktionen i teori för fuzzy-mängder, och är ett sätt att ta itu med ovanstående kritik av fuzzy-uppsättningar av typ 1 direkt. Och, om det inte finns någon osäkerhet, reduceras en otydlig uppsättning av typ 2 till en otydlig uppsättning av typ 1, vilket är analogt med att sannolikheten reduceras till determinism när oförutsägbarheten försvinner.
Typ1 fuzzy-system arbetar med en fast medlemsfunktion , medan i typ-2 fuzzy-system är medlemsfunktionen fluktuerande. En fuzzy-uppsättning bestämmer hur indatavärden omvandlas till fuzzy variabler.
Översikt
För att symboliskt skilja mellan en fuzzy-uppsättning av typ-1 och en fuzzy-uppsättning av typ-2, sätts en tilde-symbol över symbolen för den fuzzy uppsättningen; så, A betecknar en fuzzy-uppsättning av typ 1, medan à betecknar den jämförbara fuzzy-uppsättningen av typ-2. När det senare är gjort kallas det resulterande fuzzy-setet av typ 2 för ett "allmänt fuzzy-set av typ-2" (för att skilja det från det speciella intervallet med fuzzy typ-2).
Zadeh slutade inte med suddiga uppsättningar av typ 2, för i den tidningen från 1976 generaliserade han också allt detta till fuzzy set av typ n . Den här artikeln fokuserar endast på fuzzy uppsättningar av typ 2 eftersom de är nästa steg i den logiska utvecklingen från typ-1 till typ- n fuzzy uppsättningar, där n = 1, 2, ... . Även om vissa forskare börjar utforska otydliga uppsättningar av högre än typ 2, är detta arbete i början av 2009 i sin linda.

Medlemskapsfunktionen för en allmän typ-2 fuzzy uppsättning, Ã, är tredimensionell (Fig. 1), där den tredje dimensionen är värdet av medlemskapsfunktionen vid varje punkt på dess tvådimensionella domän som kallas dess "footprint" av osäkerhet"(FOU).
För en fuzzy-uppsättning av typ 2-intervall är det tredje dimensionsvärdet detsamma (t.ex. 1) överallt, vilket innebär att ingen ny information finns i den tredje dimensionen av en fuzzy-uppsättning av typ-2-intervall. Så för en sådan uppsättning ignoreras den tredje dimensionen, och endast FOU används för att beskriva den. Det är av denna anledning som en fuzzy-uppsättning av typ 2-intervall ibland kallas en första ordningens osäkerhetsmodell för fuzzy uppsättning, medan en allmän fuzzy-uppsättning av typ 2 (med dess användbara tredje dimension) ibland kallas en andra ordningens osäkerhet fuzzy set modell.
FOU representerar suddigheten av en typ-1 medlemskapsfunktion och beskrivs fullständigt av dess två begränsningsfunktioner (fig. 2), en nedre medlemskapsfunktion (LMF) och en övre medlemskapsfunktion (UMF), som båda är typ- 1 luddiga set! Följaktligen är det möjligt att använda typ-1 fuzzy set-matematik för att karakterisera och arbeta med intervall typ-2 fuzzy sets. Detta innebär att ingenjörer och forskare som redan känner till otydliga uppsättningar av typ 1 inte kommer att behöva investera mycket tid i att lära sig om generell matematik för fuzzy uppsättningar av typ 2 för att förstå och använda intervalluppsättningar av fuzzy uppsättningar av typ 2.
Arbetet med otydliga uppsättningar av typ 2 försvann under 1980-talet och början till mitten av 1990-talet, även om ett litet antal artiklar publicerades om dem. Folk försökte fortfarande ta reda på vad de skulle göra med fuzzy set av typ 1, så även om Zadeh föreslog fuzzy set av typ 2 1976, var tiden inte rätt för forskare att släppa vad de gjorde med fuzzy set av typ 1 för att fokus på fuzzy set av typ 2. Detta förändrades under den senare delen av 1990-talet som ett resultat av Jerry Mendel och hans elevs arbeten om typ 2 fuzzy set och system. Sedan dess har fler och fler forskare runt om i världen skrivit artiklar om typ 2 fuzzy set och system.
Intervall typ-2 fuzzy set
Intervall typ-2 fuzzy set har fått mest uppmärksamhet eftersom matematiken som behövs för sådana uppsättningar – främst intervall aritmetik – är mycket enklare än matematiken som behövs för allmänna typ-2 fuzzy sets. Så, litteraturen om intervall typ-2 fuzzy set är stor, medan litteraturen om allmänna typ-2 fuzzy set är mycket mindre. Båda typerna av luddiga uppsättningar undersöks aktivt av ett ständigt växande antal forskare runt om i världen och har resulterat i framgångsrik anställning inom en mängd olika domäner som robotstyrning.
Formellt har följande redan utarbetats för intervalltyp-2 fuzzy set:
- Fuzzy set operationer : union, korsning och komplement
- Centroid (en mycket allmänt använd operation av utövare av sådana uppsättningar, och också ett viktigt osäkerhetsmått för dem)
- Andra osäkerhetsmått [fuzziness, kardinalitet , varians och skevhet och osäkerhetsgränser
- Likhet
- Undergrupp
- Inbäddade fuzzy set
- Fuzzy set ranking
- Luddrig regelrankning och urval
- Typreduktionsmetoder
- Avfyrningsintervall för ett intervalltyp-2 fuzzy logic-system
- Luddigt vägt genomsnitt
- Språkligt vägt medelvärde
- Syntetisera en FOU från data som samlas in från en grupp av försökspersoner
Intervall typ 2 fuzzy logiksystem
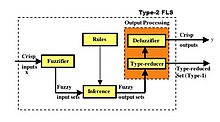
Fuzzy-uppsättningar av typ 2 finner mycket bred tillämpbarhet i regelbaserade fuzzy-logiksystem (FLS) eftersom de låter osäkerheter modelleras av dem, medan sådana osäkerheter inte kan modelleras av fuzzy-uppsättningar av typ 1. Ett blockschema över en typ 2 FLS visas i fig . 3. Denna typ av FLS används i fuzzy logic control, fuzzy logic signalbehandling, regelbaserad klassificering, etc., och kallas ibland för en funktionsapproximationsapplikation av luddiga uppsättningar, eftersom FLS är designad för att minimera en felfunktion.
Följande diskussioner, om de fyra komponenterna i fig. 3 regelbaserad FLS, ges för en intervall typ-2 FLS, eftersom de hittills är den mest populära typen av typ-2 FLS; Men de flesta diskussionerna är också tillämpliga för en allmän typ-2 FLS.
Regler, som antingen tillhandahålls av ämnesexperter eller extraheras från numeriska data, uttrycks som en samling OM-DÅ-påståenden, t.ex.
- OM temperaturen är måttlig och trycket är högt , vrid sedan ventilen en bit åt höger .
Luddiga uppsättningar är associerade med termerna som förekommer i antecedenten (IF-delen) eller följderna (THEN-delen) av regler, och med ingångarna till och utgångarna från FLS. Medlemskapsfunktioner används för att beskriva dessa fuzzy set, och i en typ-1 FLS är de alla typ-1 fuzzy set, medan i en intervall typ-2 FLS minst en medlemskapsfunktion är en intervall typ-2 fuzzy set.
En intervall typ-2 FLS låter någon eller alla av följande typer av osäkerheter kvantifieras:
- Ord som används i föregångar och följder av regler – eftersom ord kan betyda olika saker för olika människor.
- Osäkra konsekvenser – för när regler erhålls från en expertgrupp blir konsekvenserna ofta olika för samma regel, det vill säga att experterna inte nödvändigtvis är överens.
- Medlemskapsfunktionsparametrar – för när dessa parametrar optimeras med hjälp av osäkra (brusiga) träningsdata blir parametrarna osäkra.
- Bullriga mätningar — för mycket ofta är det sådana mätningar som aktiverar FLS.
I fig. 3 omvandlas uppmätta (skarpa) ingångar först till fuzzy sets i Fuzzifier- blocket eftersom det är fuzzy sets och inte nummer som aktiverar reglerna som beskrivs i termer av fuzzy set och inte nummer. Tre sorters luddgivare är möjliga i en intervalltyp-2 FLS. När måtten är:
- Perfekt, de är modellerade som ett skarpt set;
- Bullriga, men ljudet är stationärt, de är modellerade som en typ-1 fuzzy set; och,
- Bullriga, men bruset är icke-stationärt, de är modellerade som en intervalltyp-2 fuzzy-uppsättning (denna senare typen av fuzzifiering kan inte göras i en typ-1 FLS).
I fig. 3, efter att mätningarna har gjorts suddiga, mappas de resulterande inmatade fuzzy-uppsättningarna till fuzzy output-uppsättningar av inferensblocket . Detta åstadkoms genom att först kvantifiera varje regel med hjälp av fuzzy set theory, och sedan använda matematiken för fuzzy sets för att fastställa utdata från varje regel, med hjälp av en inferensmekanism. Om det finns M regler kommer de otydliga indatauppsättningarna till inferensblocket endast att aktivera en delmängd av dessa regler, där delmängden innehåller minst en regel och vanligtvis mycket färre än M regler. Slutsatsen görs en regel i taget. Så vid utgången av inferensblocket kommer det att finnas en eller flera fuzzy output-uppsättningar av avfyrade regler .
I de flesta tekniska tillämpningar av en FLS behövs ett nummer (och inte en suddig uppsättning) som dess slutliga utdata, t.ex. är följden av regeln ovan "Vrid ventilen en bit åt höger." Ingen automatisk ventil kommer att veta vad detta betyder eftersom "en bit till höger" är ett språkligt uttryck, och en ventil måste vridas med numeriska värden, dvs ett visst antal grader. Följaktligen måste de otydliga uppsättningarna för avfyrade regelutdata omvandlas till ett nummer, och detta görs i blocket för utdatabearbetning i Fig. 3.
I en typ-1 FLS mappar utdatabehandling, kallad " defuzzification ", en typ-1 fuzzy uppsättning till ett nummer. Det finns många sätt att göra detta på, t.ex. beräkna föreningen av fuzzy-uppsättningarna för utmatning av avfyrade regler (resultatet är en annan fuzzy-uppsättning av typ 1) och beräkna sedan tyngdpunkten för medlemskapsfunktionen för den uppsättningen; beräkna ett viktat medelvärde av tyngdpunkterna för var och en av de avfyrade regelns påföljande medlemskapsfunktioner; etc.
Saker och ting är något mer komplicerade för en intervall typ-2 FLS, eftersom att gå från en intervall typ-2 fuzzy set till ett nummer (vanligtvis) kräver två steg (fig. 3). Det första steget, som kallas "typ-reduktion", är där en intervall typ-2 fuzzy set reduceras till en intervallvärderad typ-1 fuzzy set. Det finns lika många typreduktionsmetoder som det finns typ 1 defuzzifieringsmetoder. En algoritm utvecklad av Karnik och Mendel nu känd som "KM-algoritmen" används för typreduktion. Även om denna algoritm är iterativ är den väldigt snabb.
Det andra steget i utdatabearbetning, som sker efter typreduktion, kallas fortfarande "defuzzification". Eftersom en typreducerad uppsättning av en otydlig intervalluppsättning av typ 2 alltid är ett ändligt intervall av tal, är det defuzzifierade värdet bara medelvärdet av de två slutpunkterna för detta intervall.
Det framgår av fig. 3 att det kan finnas två utgångar till ett intervall typ-2 FLS — skarpa numeriska värden och den typreducerade uppsättningen. Den senare ger ett mått på de osäkerheter som har flödat genom intervallet typ-2 FLS, på grund av de (eventuellt) osäkra ingångsmätningarna som har aktiverat regler vars antecedents eller följder eller båda är osäkra. Precis som standardavvikelse används i stor utsträckning i sannolikhet och statistik för att ge ett mått på oförutsägbar osäkerhet kring ett medelvärde, kan den typreducerade uppsättningen ge ett mått på osäkerhet om den skarpa uteffekten av en intervall typ-2 FLS.
Dator med ord
En annan applikation för fuzzy set har också inspirerats av Zadeh — "Computing with Words". Olika akronymer har använts för "beräkna med ord", t.ex. CW och CWW. Enligt Zadeh:
- CWW är en metod där beräkningsobjekten är ord och propositioner hämtade från ett naturligt språk. [Den är] inspirerad av den anmärkningsvärda mänskliga förmågan att utföra en mängd olika fysiska och mentala uppgifter utan några mätningar och några beräkningar.
Naturligtvis menade han inte att datorer faktiskt skulle använda ord – enstaka ord eller fraser – snarare än siffror. Han menade att datorer skulle aktiveras av ord, som skulle omvandlas till en matematisk representation med hjälp av fuzzy uppsättningar och att dessa fuzzy uppsättningar skulle mappas av en CWW-motor till någon annan fuzzy uppsättning varefter den senare skulle omvandlas tillbaka till ett ord. En naturlig fråga att ställa är: Vilken sorts luddig uppsättning – typ-1 eller typ-2 – ska användas som modell för ett ord? Mendel har hävdat, på basis av Karl Poppers koncept om " falsifikationism ", att det är vetenskapligt felaktigt att använda en fuzzy-uppsättning av typ 1 som modell för ett ord. En intervalltyp-2 fuzzy set bör användas som en (första ordningens osäkerhet) modell för ett ord. Mycket forskning pågår om CWW.
Ansökningar
Typ-2 fuzzy set användes i följande områden:
- Bildbehandling
- Videobehandling och datorseende
- Felläge och effektanalys
- Funktionsapproximation och uppskattning
- Kontrollsystem
programvara
Freeware MATLAB-implementeringar, som täcker allmänna och intervall typ-2 fuzzy set och system, såväl som typ-1 fuzzy system, finns tillgängliga på: http://sipi.usc.edu/~mendel/software . Programvara som stöder diskreta intervalltyp-2 fuzzy logic-system finns tillgänglig på: DIT2FLS Toolbox - http://dit2fls.com/projects/dit2fls-toolbox/ DIT2FLS Library Package - http://dit2fls.com/projects/dit2fls-library-package /
Java-bibliotek inklusive källkod för typ-1, intervall- och allmänna typ-2 fuzzy-system finns tillgängliga på: http://juzzy.wagnerweb.net/ .
Python-biblioteket för typ 1 och typ 2 fuzzy set finns tillgängligt på: https://github.com/carmelgafa/type2fuzzy
Python-bibliotek för intervalltyp 2 fuzzy set och system finns tillgängligt på: https://github.com/Haghrah/PyIT2FLS
En öppen källkod Matlab/Simulink Toolbox för Interval Type-2 Fuzzy Logic Systems finns tillgänglig på: http://web.itu.edu.tr/kumbasart/type2fuzzy.htm
Se även
- Beräkningsintelligens
- Expertsystem
- Luddigt kontrollsystem
- Rolig logik
- Luddigt set
- Granulär datoranvändning
- Perceptuell beräkning
- Grovt set
- Mjukt set
- Vaghet
- Slumpmässig-fuzzy variabel
externa länkar
Det finns två IEEE Expert Now multimediamoduler som kan nås från IEEE på: http://www.ieee.org/web/education/Expert_Now_IEEE/Catalog/AI.html
- "Introduction to Type-2 Fuzzy Sets and Systems" av Jerry Mendel, sponsrad av IEEE Computational Intelligence Society
- "Type-2 Fuzzy Logic Controllers: Towards a New Approach for Handling Uncertainties in Real World Environments" av Hani Hagras, sponsrad av IEEE Computational Intelligence Society