Tvådimensionellt filter

Tvådimensionella filter har haft betydande utvecklingsansträngningar på grund av deras betydelse och höga tillämpbarhet inom flera domäner. I 2-D-fallet är situationen helt annorlunda än 1-D-fallet, eftersom de flerdimensionella polynomen i allmänhet inte kan faktoriseras. Detta betyder att en godtycklig överföringsfunktion i allmänhet inte kan manipuleras till en form som krävs av en viss implementering. Ingångs-utgångsförhållandet för ett 2-D IIR-filter följer en linjär partiell differensekvation med konstant koefficient från vilken värdet på ett utmatningssampel kan beräknas med användning av ingångssamplen och tidigare beräknade utsampler. Eftersom värdena för utsamplen återkopplas kan 2-D-filtret, liksom dess 1-D-motsvarighet, vara instabilt.

Motivation och tillämpningar

På grund av den snabba utvecklingen av informationsvetenskap och datorteknik har teorin om design och tillämpning av digitala filter tagit ett steg framåt. Vi möter en mängd olika signaler i verkligheten, såsom sändningssignaler , tv- signaler, radarsignaler , mobiltelefonsignaler , navigationssignaler , radioastronomisignaler , biomedicinska signaler, styrsignaler, vädersignal, seismisk signal, mekanisk vibrationssignal, fjärrkontroll avkännings- och telemetrisignaler , etc. De flesta av dessa signaler är analoga signaler och bara en liten del av dem är digitala signaler. De analoga signalerna är en kontinuerlig funktion av de oberoende variablerna , som kan vara endimensionella, tvådimensionella eller flerdimensionella. I de flesta fall är variabeln för endimensionella analoga signaler tid. Efter tidssamplingen och diskretiseringen av storleken kommer en sådan analog signal att bli en endimensionell digital signal. Den resulterande digitala signalen kan representeras av en diskret sekvens. Till exempel är en vanlig signal röstsignal. Ett exempel på en tvådimensionell signal är en bild. Ett filter är ett system som kan omvandla en signal till en annan signal. Exempel på sådan transformation inkluderar utjämning av signalen för brusborttagning, borttagning av frekvenskomponenter från en signal och förstärkning av frekvenskomponenter för signalförbättring. Utformningen och implementeringen av filter är en viktig gren inom signalanalys och signalbehandlingsteknik. Filter spelar också en huvudroll vid signalinsamling, överföring, bearbetning och utbyte.

Problemformulering & grundläggande begrepp

Digitala filter

Digital signalfiltrering implementerar ett digitalt filter. Ett digitalt filter är ett system som utför matematiska operationer på en samplade, tidsdiskret signal för att reducera eller förbättra vissa aspekter av den signalen. In- och utsignalerna är alla digitala signaler. Detta är i motsats till den andra stora typen av elektroniskt filter, det analoga filtret, som är en elektronisk krets som arbetar på en kontinuerlig analog signal . Egentligen är det grundläggande konceptet för digitala filter och analoga filter detsamma. Den enda skillnaden är typerna av signaler och metoderna för att filtrera. Digitala filter kan implementeras numeriskt i mjukvara och har fördelarna med hög bearbetningsnoggrannhet, stadigt system, liten volym och låg vikt. Det finns ingen impedansmatchning i digitala filter och digitala filter kan åstadkomma vissa speciella filtreringsfunktioner som inte kan åstadkommas med analoga filter. Analoga signaler kan också bearbetas genom digitala filter genom att använda analog till digital omvandlare .

Tvådimensionella digitala filter

Tvådimensionella filter används för att behandla tvådimensionella digitala signaler. Det finns en viktig skillnad mellan utformningen av 1-D och 2-D digitala filterproblem. I 1-D fall kan designen och implementeringen av filter lättare övervägas separat. Filtret kan först utformas och sedan, genom lämpliga manipulationer av överföringsfunktionen, kan de koefficienter som krävs av en speciell nätverksstruktur bestämmas. Medan i 2D-fallet är design och implementering närmare relaterade. Eftersom flerdimensionella polynom inte kan faktoriseras i allmänhet. Detta betyder att en godtycklig flerdimensionell överföringsfunktion i allmänhet inte kan manipuleras till en form som krävs av en viss implementering. Om vår implementering endast kan realisera faktorable överföringsfunktioner, måste vår designalgoritm skräddarsys för att endast designa filter av denna klass. Detta har effekten att komplicera designproblemet och även begränsa antalet praktiska implementeringar. Digitala filter kan kategoriseras i två huvudtyper, nämligen finit impulsrespons ( FIR ) och oändlig impulsrespons ( IIR ). 2-D FIR digitalt filter uppnås av en icke-rekursiv algoritmstruktur medan 2-D IIR digitalt filter uppnås av en rekursiv återkopplingsalgoritmstruktur.

Befintliga tillvägagångssätt

Direkt formimplementering av 2-D IIR-filter

Ett IIR-filter kan implementeras i direkt form genom att omarrangera dess differensekvation för att uttrycka ett utgångssampel i termer av ingångssamplen och tidigare beräknade utgångssamplen. För ett första kvadrantfilter, insignalen $x\left(n_{1},n_{2}\right)$ och utsignalen $y\left(n_{1},n_{2}\right)$ är relaterade till

$y\left(n_{1},n_{ 2}\right)=\summa _{l_{1}=0}^{L_{1}-1}\summa _{l_{2}=0}^{L_{2}-1}a(l_{ 1},l_{2})x(n_{1}-l_{1},n_{2}-l_{2})-\summa _{k_{1}=0}^{K_{1}-1 }\summa _{k_{2}=0}^{K_{2}-1}b(k_{1},k_{2})y(n_{1}-k_{1},n_{2}- k_{2})$

Eftersom filtrets svar på en impuls $\delta (n_{1},n_{2})$ per definition är impulssvaret ${\ displaystyle h\left(n_{1},n_{2}\right)}$ , vi kan härleda förhållandet

$h\left(n_{1},n_{2}\right)=a(l_{1},l_{2})-\summa _{k_{1}=0} ^{K_{1}-1}\summa _{k_{2}=0}^{K_{2}-1}b(k_{1},k_{2})h(n_{1}-k_{ 1},n_{2}-k_{2})$

Genom att ta 2-D z-transformen på båda sidorna kan vi lösa systemfunktionen ${\displaystyle H\left(z_{1},z_{2}\right)} ,$ som ges av

$H_{z}(z_{1},z_{2})={\frac {\sum _{l_{1}=0}^{L_{1}-1}\summa _{l_{2}=0 }^{L_{2}-1}a(l_{1},l_{2})z_{1}^{-l_{1}}z_{2}^{-l_{2}}}{\summa _{k_{1}=0}^{K_{1}-1}\summa _{k_{2}=0}^{K_{2}-1}b(k_{1},k_{2}) z_{1}^{-k_{1}}z_{2}^{-k_{2}}}}={\frac {A_{z}(z_{1},z_{2})}{B_{ z}(z_{1},z_{2})}}$

Detta förhållande kan ses som ett resultat av kaskaden av två filter, ett FIR-filter med en systemfunktion lika med $A(z_{1},z_{2})$ och en IIR filter med en systemfunktion lika med ${\displaystyle 1/B(z_{1},z_{2})} ,$ som visas i figuren nedan.

Representation för filtret med systemfunktionen $H(z_{1},z_{2})$ . Anpassad från [3].

Parallella implementeringar av 2-D IIR-filter

En annan metod för att bygga upp komplicerade 2-D IIR-filter är genom att parallellkoppla underfilter. I detta fall blir den övergripande överföringsfunktionen

$H_{z}^{p}(z_{1},z_{2}) =\summa _{i=1}^{N}H_{z}^{(i)}(z_{1},z_{2})$

Använder ekvation

$H_{z}^{(i)} (z_{1},z_{2})={\frac {A_{z}^{(i)}(z_{1},z_{2})}{B_{z}^{(i)}( z_{1},z_{2})}}$

och sätter summan i överföringsfunktionen över en gemensam nämnare, får vi den utökade formen

$H_{z}^{p}(z_{1},z_ {2})={\frac {A_{z}^{p}(z_{1},z_{2})}{B_{z}^{p}(z_{1},z_{2})} }={\frac {\sum _{j=1}^{N}\prod _{i\neq j}A_{z}^{(j)}(z_{1},z_{2})B_{ z}^{(i)}(z_{1},z_{2})}{\prod _{i=1}^{N}B_{z}^{(i)}(z_{1},z_ {2})}}$

Den parallella formen kan inte användas för att implementera en godtycklig 2-D rationell systemfunktion. Ändå kan vi syntetisera intressanta 2-D IIR-filter som kan implementeras av en parallell arkitektur. Till exempel kan den parallella formen vara fördelaktig när man designar ett filter med flera passband . Den parallella implementeringen kan också vara användbar för att implementera ett 2-D IIR- filter vars impulssvar inte är begränsat till en enda kvadrant, såsom ett symmetriskt filter.

Parallell sammankoppling av N enkla 2-D IIR-filter för att bilda ett nytt 2-D IIR-filter. Anpassad från [3].

Design av 2-D IIR-filter med genetisk algoritm

Många designtekniker för 2-D IIR digitala filter har rapporterats i litteraturen. 2013 genetisk algoritm framgångsrikt använts för digital filterdesign i ungefär ett decennium. Här presenterar vi en metod för att designa 2-D IIR-filter som kallas GA-baserad designmetod.

Initialisering

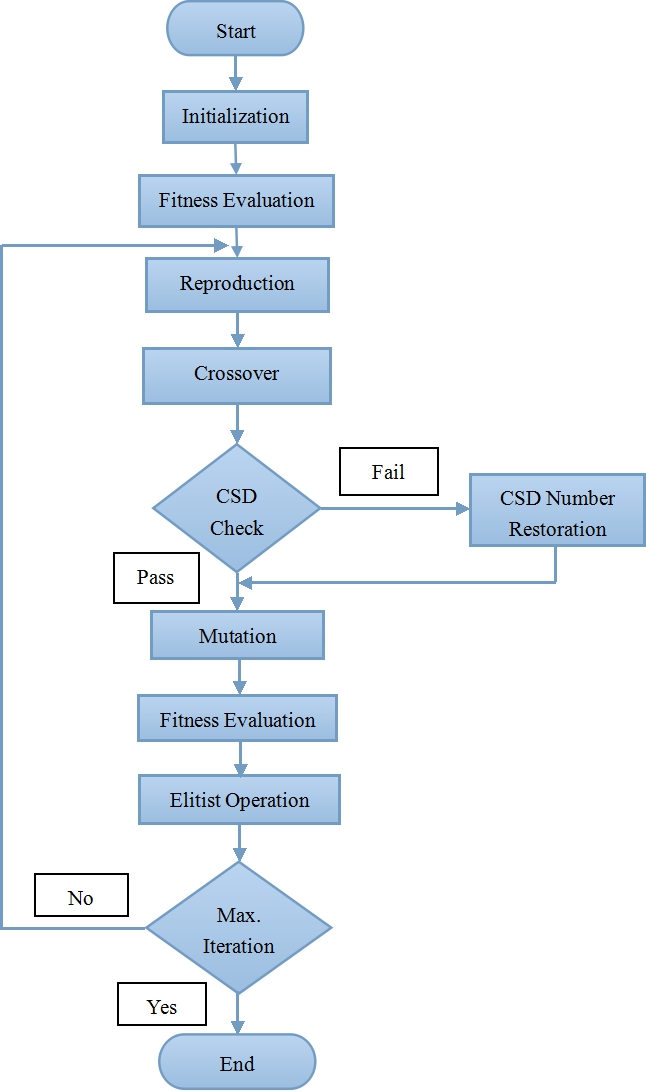
Figuren nedan visar det föreslagna GA-baserade designflödet. Filterkoefficienter är kodade i deras CSD-nummerrepresentation. I populationsinitieringen genereras kromosomer slumpmässigt. Varje koefficient har den fördefinierade ordlängden och det maximala antalet siffror som inte är noll, som kan ställas in på valfritt önskat värde.

GA-baserat designflödesschema. Anpassad från [5].

Genetiska operatörer

Roulette Wheel Selection används som reproduktionsoperatör. Efter varje övergångsoperation kontrolleras koefficienten där övergångspunkten ligger i CSD-formatet. Mutationsoperationen är den enkla enbitsflipningen. Efter mutation kontrolleras varje koefficient i avkomman på CSD-format.

Konditionsutvärdering och ersättningsstrategi

Konditionsutvärderingen är en process i två steg. Det första steget är att kontrollera stabiliteten för varje andra ordningens sektion med hjälp av stabilitetstriangeln. Kromosomer som inte klarar kontrollen tilldelas konditionsvärdet 0. Elitistisk strategi tillämpas för gamla generationens ersättning. Efter reproduktion hittas den bästa kromosomen och den sämsta kromosomen hos avkomman. Det designade filtret har en icke-separerbar täljare och separerbar nämnaröverföringsfunktion . Nummeråterställningstekniken används för att säkerställa att filterkoefficienterna representeras i det fördefinierade CSD-formatet.